典型的断裂力学参数有能量释放率及裂纹尖端的应力幅值和位移场。下面的参数被广泛应用于断裂力学分析中。

●应力强度因子。

●能量释放率。

●J积分。

应力强度因子和能量释放率只适用于线弹性断裂力学。J积分对于线弹性和非线性弹-塑性材料均适用。

1.应力强度因子

对于线弹性材料，裂纹尖端的应力、应变场表达式为：

式中，K是应力强度因子，r和θ为极坐标系（见图18-2）的坐标。上面的方程对三种断裂模式都适用。对于第一种模式的断裂，应力场为：

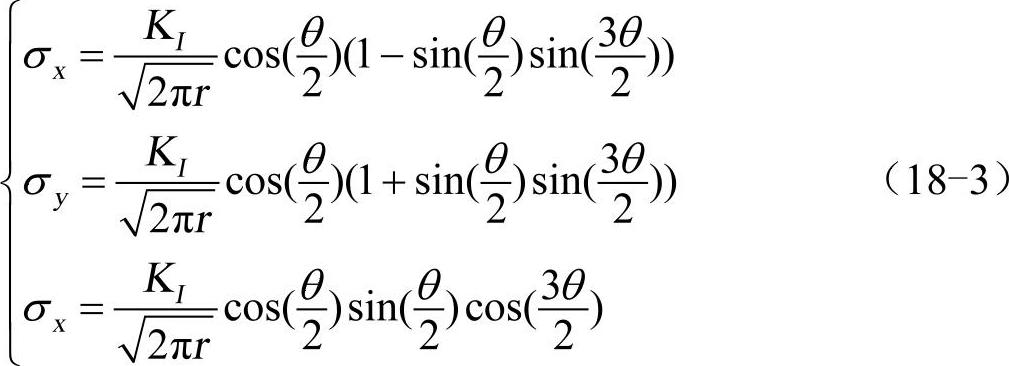
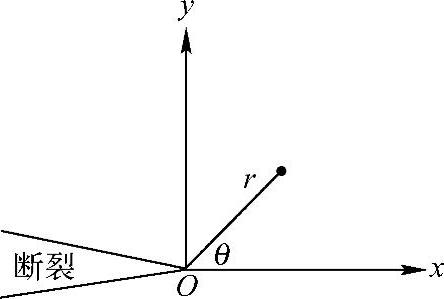
图18-2 裂纹尖端示意图

应力张量因子和能量释放率通过下式建立联系：

式中，G表示能量释放率，对于平面应变，有：(www.daowen.com)

对于平面应力，有：

E′=E （18-6）

其中，E为材料的杨氏模量；υ为泊松比。

2.J积分

J积分是弹-塑性断裂力学中最广为接受的参数之一。J积分的定义为：

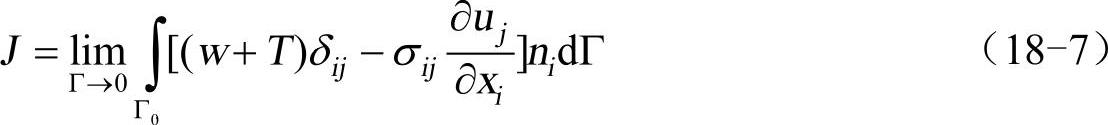
式中，w是应变能密度，T是动能密度，σ是应力，u是位移向量，Γ是积分边界。对于线弹性材料中的裂纹，J积分表示能量释放率。对于非线性材料，J积分还表示裂纹尖端的应力幅值和位移场。

Hutchinson、Rice和Rosengren独立推导出了非线性材料裂纹尖端场的J积分描述。他们都假设在塑性应变和应力之间存在指数关系。如果包含弹性应变，单轴变形关系由下式给出：

式中，σ₀是参考应力（材料的屈服应力）；ε₀=σ₀/E，α是无尺寸的常数；n是硬化分量。他们指出，在距离裂纹尖端很近的距离且完全位于塑性区内，裂纹尖端应力和裂纹尖端前的应变可以表示为：

对于弹性材料，n=1，上面的方程显示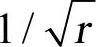奇异，这与线弹性断裂力学的结论是一致的。