1.模型的几何尺寸

本实例假设薄钢板两个方向的尺寸远大于厚度，因此可以简化为平面应变问题，又因为平面模型的左右对称性，所以只需建立平面的1/2模型，其力学模型简图如图16-22所示。图中给出了基本的模型尺寸，且薄钢板的半长为L，薄钢板的厚度为H，L₂和L₁之间存在以下关系：L₂=L₁+H，表16-1给出了模型的基本数据。

表16-1 模型的基本几何尺寸

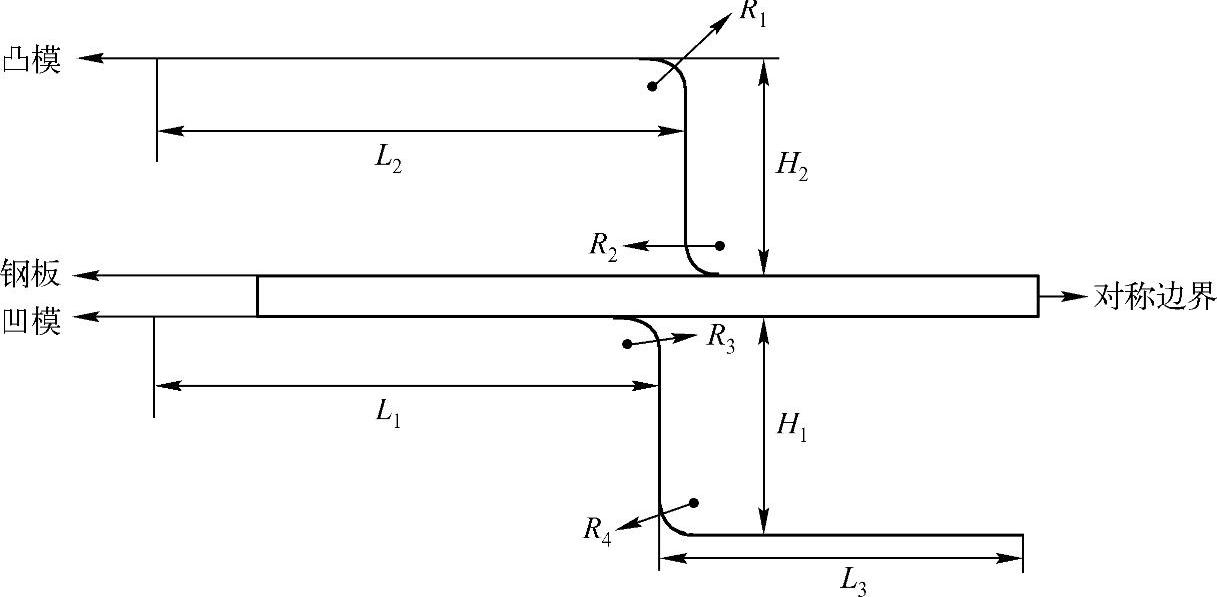
图16-22 薄板冲压的模型简图

2.单元的选择及材料常数(www.daowen.com)

因为冲压是大变形、塑性，所以本实例选用4节点平面单元PLANE42，并通过设置关键字K3实现模拟平面应变问题。凸模和凹模假设为刚性材料，通过接触向导来实现对其的定义；钢板的应力应变关系假设为双线性等向强化，各材料参数分别为弹性模型为2E11Pa，泊松比为0.3，屈服强度为200MPa，切线模量为2E9Pa，其应力应变关系如图16-23所示。

3.边界条件

本实例假设整个冲压过程为准静态，即为静力学分析并且步考虑温度的影响。固定凹模的所有自由度，在凸上约束X平移自由度和转动自由度，在凸模上施加Y方向的位移为-H1；约束薄钢板的右端面为对称约束，冲压接触后再施加Y方向位移为0.2×H2。

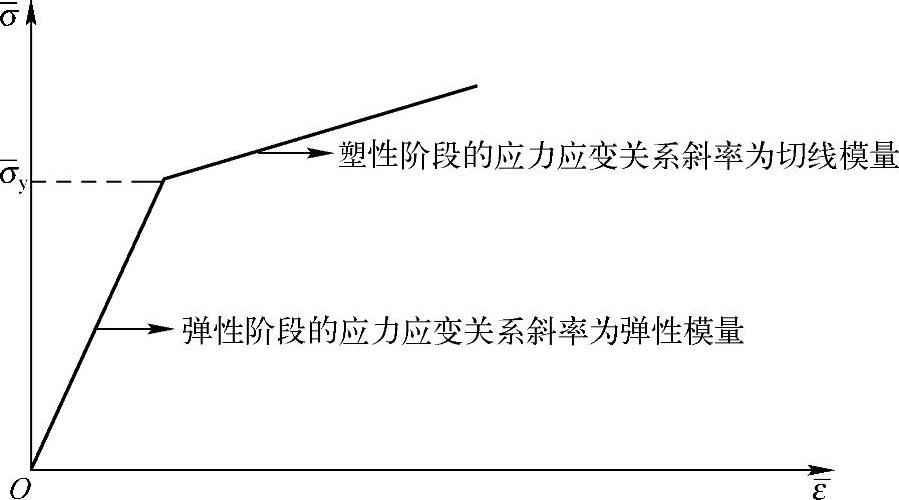
图16-23 薄钢板的应力应变关系曲线