许多常用的工程材料，在应力水平低于比例极限时，应力-应变关系为线性的。超过这一极限后，应力-应变关系变成非线性，但却不一定是非弹性的。以不可恢复的应变为特征的塑性，则在应力超过屈服点后开始出现。由于屈服极限与比例极限相差很小，ANSYS程序在塑性分析中，假设这两个点相同，见图15-10。

塑性是一种非保守的、与路径相关的现象。换句话说，载荷施加的顺序以及什么时候发生塑性响应，将影响最终求解结果。如果用户预计在分析中会出现塑性响应，则应把载荷处理成一系列的小增量载荷步或时间步，以使模型尽可能附合载荷-响应路径。最大塑性应变是在输出（Jobname.OUT）文件的子步信息中打印的。

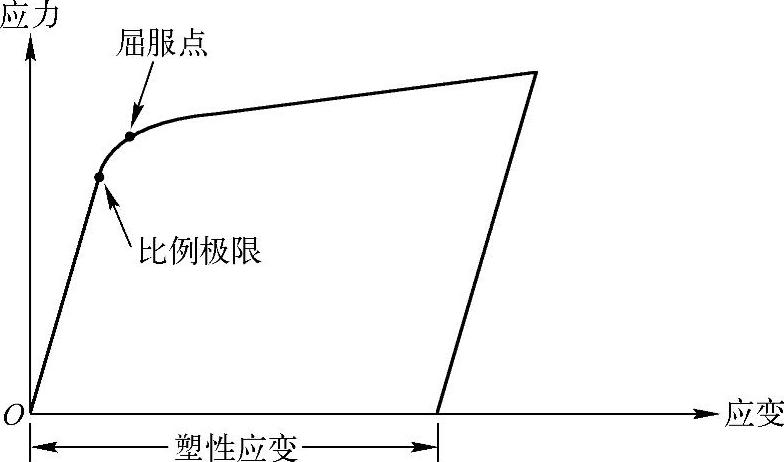
图15-10 弹塑性应力-应变曲线

在一个子步中，如果执行了大量的平衡迭代，或得到大于15%的塑性应变增量，则塑性将激活自动时间步选项。如果取了太大的时间步，则程序将二分时间步，并重新求解。

其他类型的非线性行为可以与塑性同时产生。实际上，大位移和大应变几何非线性经常伴随有塑性材料响应，如果用户预计在结构中存在大变形，则必须在分析中用NLGEOM命令激活这些效应。对于大应变分析，材料应力-应变特性必须按真实应力和对数应变输入。

1.屈服准则

对单向受拉试验，可以通过简单的比较轴向应力与材料的屈服应力来决定是否有塑性变形发生，然而，对于一般的应力状态，是否到达屈服点并不是明显的。

屈服准则是一个可以用来与单轴测试的屈服应力相比较的应力状态的标量表示。因此，知道了应力状态和屈服准则，程序就能确定是否有塑性应变产生。

在多轴应力状态下，屈服准则可以用下式来表示：

σ_e=f({σ})=σ_y （15-2）

其中，σ_e为等效应力；σ_y为屈服应力。

当等效应力超过材料的屈服应力时，将会发生塑性变形。

（1）VonMises屈服准则

VonMises屈服准则是一个比较通用的屈服准则，尤其适用于金属材料。对于VonMises屈服准则，其等效应力为：

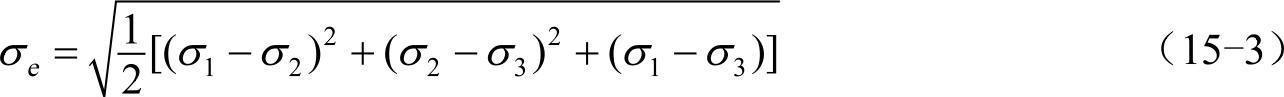
其中，σ₁，σ₂，σ₃为三个主应力。

可以在主应力空间中画出VonMises屈服准则，见图15-11。

在三维主应力空间中，VonMises屈服面是一个以σ₁=σ₂=σ₃为轴的圆柱面，在二维中，屈服面是一个椭圆，在屈服面内部的任何应力状态都是弹性的，屈服面外部的任何应力状态都会引起屈服。静水压应力状态（σ₁=σ₂=σ₃）不会导致屈服：屈服与静水压应力无关，而只与偏差应力有关，因此，σ₁=180，σ₂=σ₃=0的应力状态比σ₁=σ₂=σ₃=180的应力状态接近屈服。VonMise屈服准则是一种除了土壤和脆性材料外典型使用的屈服准则，在土壤和脆性材料中，屈服应力是与静水压应力有关的，侧限压力越高，发生屈服所需要的剪应力越大。

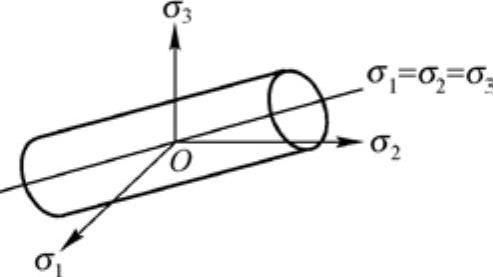
图15-11 主应力空间中的VonMises屈服面

（2）Drucker-Prager（DP）屈服准则

Drucker-prager屈服准则是对Mohr-Coulomb准则的近似，它修正了Von Mises屈服准则，即在VonMises表达式中包含一个附加项。其屈服面并不随着材料的逐渐屈服而改变，因此没有强化准则,塑性行为被假定为理想弹塑性，然而其屈服强度随着侧限压力（静水应力）的增加而相应增加，另外，这种材料考虑了由于屈服而引起的体积膨胀，但不考虑温度变化的影响。此材料选项适用于混凝土、岩石和土壤等颗粒状材料。

对DP材料，其屈服准则表达式为：

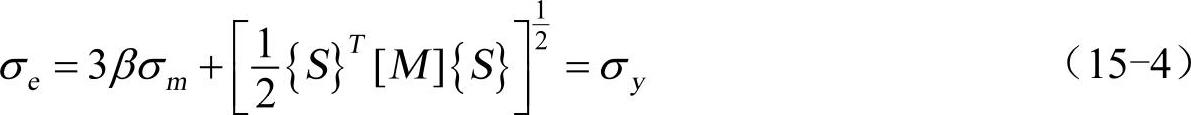
其中(www.daowen.com)

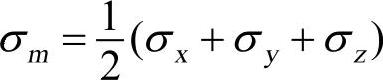；为平均应力，{S}为偏差应力。

材料常数β和屈服强度σ_y的表达式如下：

其中，φ为内摩擦角；C为粘滞力。

对DP材料，当材料参数β、σ_y给定后，其屈服面为一圆锥面，此圆锥面是六角形的摩尔－库仑屈服面的外接锥面，如图15-12所示。

2.流动准则

流动准则描述了发生屈服时，塑性应变的方向，也就是说，流动准则定义了单个塑性应变分量（ε^pl_x，ε^pl_y等）随着屈服是怎样发展的。流动准则由以下方程给出：

其中，λ是塑性乘子，决定了塑性应变量；Q为塑性势，是应力的函数，决定了塑性应变方向。

一般来说，流动方程是塑性应变在垂直于屈服面的方向发展的屈服准则中推导出来的，即Q等于屈服函数，这种流动准则叫做关联流动准则，如果使用其他的流动准则，则叫做不关联的流动准则。

3.强化准则

强化准则描述了初始屈服准则随着塑性应变的增加是怎样发展的。一般来说，屈服面的变化是以前应变历史的函数，在ANSYS程序中，使用了如下三种强化准则。

1）等向强化：是指屈服面以材料中所做塑性功的大小为基础在尺寸上扩张。对Von Mises屈服准则来说，屈服面在所有方向均匀扩张，见图15-13。

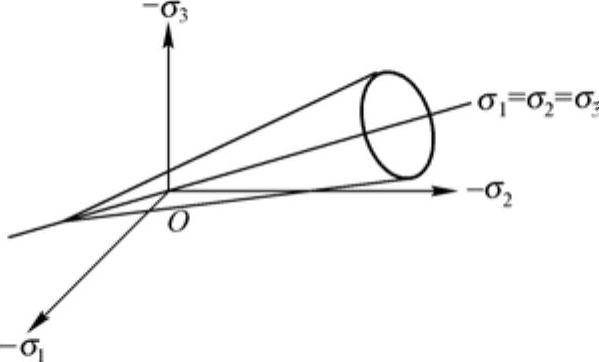
图15-12 Drucker-Prager屈服面

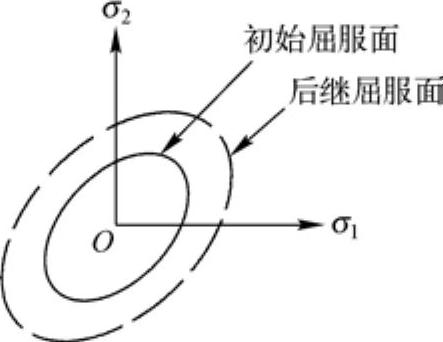
图15-13 等向强化时的屈服面变化图

由于等向强化，在受压方向的屈服应力等于受拉过程中所达到的最高应力。

2）随动强化假定屈服面的大小保持不变而仅在屈服的方向上移动，当某个方向的屈服应力升高时，其相反方向的屈服应力应该降低，见图15-14。

在随动强化中，由于拉伸方向屈服应力的增加导致压缩方向屈服应力的降低，所以在对应的两个屈服应力之间总存在一个2σ_y的差值，初始各向同性的材料在屈服后将不再是各向同性的。

3）混合强化是等向强化和随动强化的结合，屈服面不仅在大小上扩张，而且还在屈服的方向上移动，见图15-15。

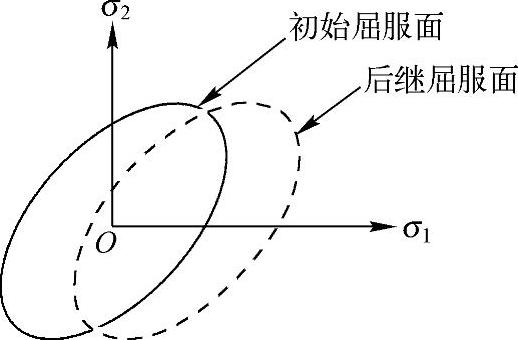
图15-14 随动强化时的屈服面变化图

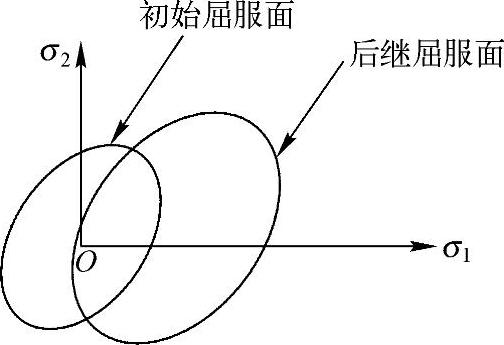
图15-15 混合强化时的屈服面变化图