如前所述，瞬态分析求解的精度取决于积分时间步长的大小——时间步长越小，精度越高。太大的积分时间步长将引发会影响较高阶模态的响应（从而影响整体响应）的误差。太小的时间积分步长将浪费计算机资源。要想计算出最优时间步长，应当遵循下列五个准则。

1.计算响应频率

由于结构的动力学响应可以看成是各阶模态响应的组合，时间步长应小到能够解出对整体响应有贡献的最高阶模态。对于Newmark时间积分方案，已经发现当时间步长的取值为20倍最高频率时会产生较合理精度级的解。也就是说，如果f表示频率（以周/单位时间为单位），积分时间步长（ITS）应为：

ITS=1/(20f) （14-5）

如果要得到加速度结果，可能要求更小的ITS值。图14-5显示了ITS值对单自由度弹簧-质量体系统周期延长量的影响。可以看到当取每周20或更多个时间点时将引起小于百分之一的周期延长。

2.计算所加载荷/时间关系曲线

响应总是倾向滞后于所施加的载荷的，特别是对于阶跃载荷，如图14-6所示。阶跃载荷在发生阶跃的时间点附近，要求采用较小的ITS以紧紧跟随载荷的阶跃步变化。要跟随阶跃载荷，ITS也许要小到和1/(180f)相近。

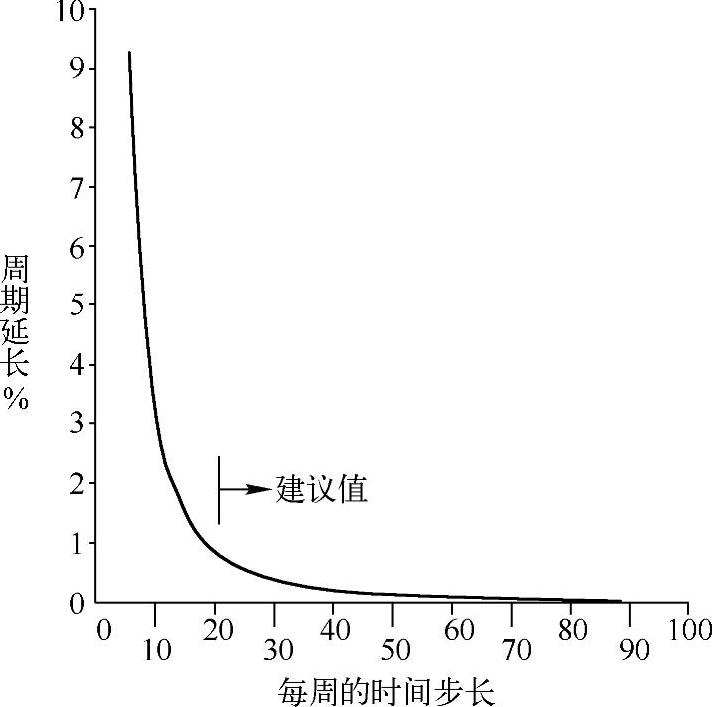
图14-5 积分时间步长对周期延长的影响

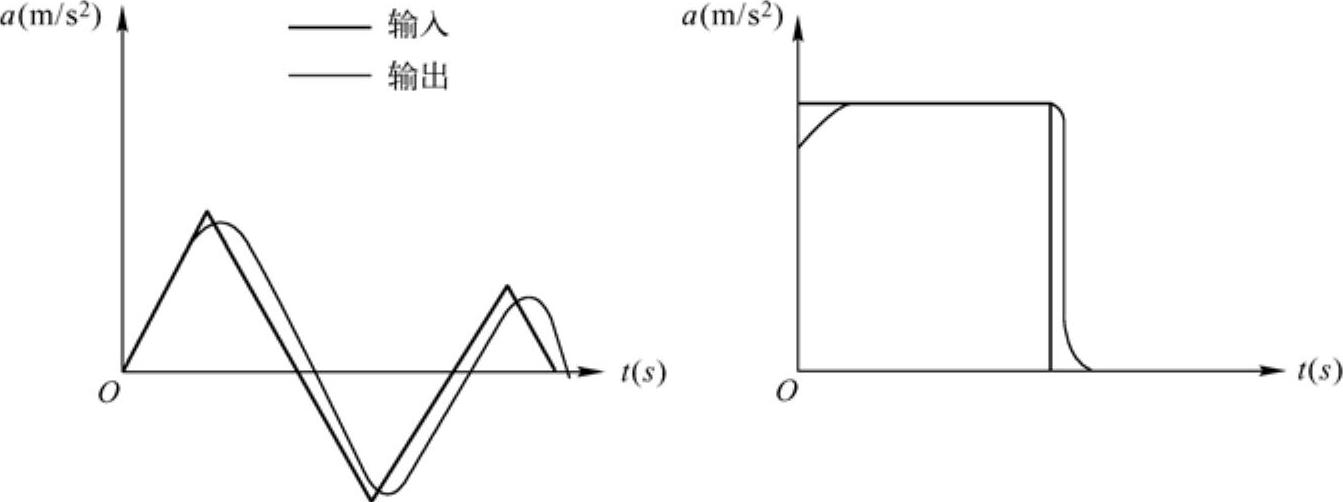
图14-6 瞬态输入/瞬态响应曲线

3.计算接触频率(www.daowen.com)

在涉及接触（碰撞）的问题中，时间步长应当小到足以捕捉到两个接触表面之间的动量传递。在计算时如果违反上述准则，将发生明显的能量损失，从而碰撞将不会是完全弹性的。积分时间步长可由接触频率（f_c）确定：

其中，k是间隙刚度；m是作用在间隙上的有效质量；N是每周的点数。

要使能量损失最小，每周至少要取30个点（N=30）。如果要得到加速度结果，可能要取更大的N值。对缩减法和模态叠加法，N必须至少为7以确保求解的稳定性。如果接触时间和接触质量比整个瞬态过程的时间和系统质量小得多，则可以在每周取少于30个点（N<30），这是因为此时能量损失对总响应的影响很小。

4.计算波传播

如果对波传播效果感兴趣，则时间步长应当小到当波在单元之间传播时足以捕捉到波动效应。

5.计算非线性

大部分问题要求满足前面四个准则的时间步长就可捕捉到非线性行为，但也有少数例外情形：当结构在载荷作用下趋于刚化（例如，从弯曲状态变化到薄膜承载状态的大变形问题），则必须求解被激活的高阶模态。

避免使用过小的时间步长，特别是建立初始条件时，因为过小的数值可能引起数值计算困难。例如，对基于时间大小的计算而言，小于相对10^-10数量级的时间步长就会引起数值计算困难。

在用合适的准则计算出时间步长后，在具体分析中应该用最小的步长值。可以采用自动时间步长来让ANSYS程序决定在求解中何时增大或减小时间步长，自动时间步长将在下面进行讨论。