瞬态动力学平衡方程：

[M{u}）][{Cu＆}++][K][u}{=P^a} (14-1)

其中，[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{u}为节点加速度向量；{u}为节点速度向量；{u}为节点位移向量。

在任意给定的时间t，这些方程可以看做是一系列考虑了惯性力[M]{u}和阻尼力[C]{u}的静力学平衡方程。ANSYS里使用两种方法求解方程(14-1)：向前差分时间积分和Newmark积分（包括将之改进后的HHT算法）。向前差分方法适用于求解显式的瞬态分析。Newmark和HHT方法使用隐式方法来求解瞬态问题。

Newmark求解方法的无条件稳定必须满足：

Newmark参数根据下式输入：(www.daowen.com)

其中，γ为振幅衰减因子。

无条件稳定也可以表述为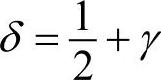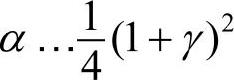，并且γ…0。因此只要γ…0，则求解就是稳定的。对于压电分析将参数设置为α=0.25，δ=0.5并且θ=0.5。通常情况下衰减因子γ=0.005。当γ=0时（即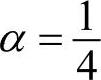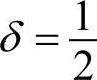，时）Newmark方法为平均加速度法。由于平均加速度法在位移幅值误差方面不产生任何数值阻尼。如果其他方面也没有阻尼，缺乏数值阻尼在高频结构计算中会产生不可接受的数值噪声。因此需要有一定水平的数值阻尼并且期望通过设置γ>0来实现。

因此，ANSYS提供了HHT方法，该方法具备以下特征：在高频下引进数值阻尼不会降低求解精度，在低频下不会产生过多的数值阻尼。从而达到瞬态动力学计算的需要。

在HHT方法中通过两个连续步长的线性组合来实现瞬态动力学的平衡方程。α_m和α_f是两个额外的参数，在给定幅值衰减因子γ时，其余四个参数为：

ANSYS中提供了三种方法求解（14-1）式，下面将为读者详细加以介绍。