每次随机振动循环都对累积损伤具有贡献，当总的累积损伤达到100%时就表示发生了失效，并且随机疲劳和确定性疲劳分析在理论上是相同的。对于恒定应力幅的周期载荷作用下的应力历程，波动应力的每次循环都会在材料中产生小的变化，从而产生微小裂缝并不断发展。应力幅值越大，每经过一次循环裂缝增长得就越快越多。随着应力循环次数的不断增加，累积损伤不断增多，直至发生失效。对于恒定应力幅，疲劳失效允许的循环次数是按材料的疲劳（S-N）曲线进行确定的。一般工程材料的S-N曲线是对数S-N曲线，在坐标图上近似为一条直线，近似的数学公式为：

NS^b=c （13-1）

其中，N为应力幅对应的最大循环次数；S为应力幅；b为对于大多数材料，取值范围在5～20之间的常数；c为常数，其值取决于材料的性质。

当应力历程是随机过程而不是固定幅值时，疲劳计算相对比较复杂困难，但已经有许多种处理方法可以解决这个问题，这里介绍其中的两种方法：①Steinberg提出的比较简化方法，即三区间法，它广泛用于航天电子工业中；（2）Crandall和Mark提出的更精确的方法，即基于随机振动结果的Miner方法。像Miner定律的线性累积损伤假设一样，这两种方法都是基于固定振幅的，假定应力幅循环了n次时，消耗了材料疲劳寿命的n/N部分，而其他应力水平的循环也以相同方式对材料产生部分损伤。如果应力幅S_i的循环次数n_i没有达到对应的许可次数N_i，那么产生的累积损伤为：

当D=1时，表示疲劳寿命已经耗尽，预测发生了疲劳破坏。考虑到该假设的不精确性和缺点，有时也假设累积损伤D为小于1的常数时也会发生疲劳破坏。

Crandall和Mark提出的基于随机振动结果的Miner方法的假设前提是一个典型的窄带随机过程。随机过程中应力幅在每次循环下的大小不一致，从而对总体累积损伤的贡献也就大小不一致。假定随机过程的时刻T对应的总体累积损伤为D(T)，当T=T_F时总体损伤达到1并预测疲劳发生。

假定ν₀⁺表示单位时间内正交零点的平均数目（即频率），那么在时间T内循环的数目为ν₀⁺T，对应的总体损伤期望值为：

其中，p(a)da表示幅值在a和a+da间的循环部分次数；p(a)为应力幅值的峰值概率密度；N(a)为幅值a所对应的允许循环次数。

期望的损伤是基于峰值的分布p(a)。对于正态分布数据，峰值满足瑞利（Rayleigh）分布，这样将上式中p(a)换成瑞利密度函数，利用S-N关系式替换N(a)，那么总体损伤期望值变成：

其中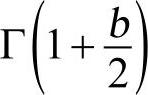，为χ（gamma）函数；b与c为前面讲述的疲劳曲线公式中的常数。另外，Steinberg提出了更加简单的基于高斯分布的三区间法，它表示：68.3%的时间应力值在-1σ～+1σ之间；

95.4%的时间应力值在-2σ～+2σ之间；

99.73%的时间应力值在-3σ～+3σ之间。

因而，在利用Miner定律进行疲劳计算时，可以将应力可以处理成3个区间：(www.daowen.com)

应力区间发生的时间

-1σ～+1σ68.3%的时间；

-2σ～+2σ27.1%的时间；

-3σ～+3σ4.33%的时间；

该方法的前提是，大于3σ的应力仅仅发生在（100-99.73）0.27%的时间内，假定它们不造成任何损伤。这样，利用Miner定律进行疲劳计算，总体损伤的计算公式是：

其中，n_1σ为等于或低于1σ水平的实际循环数目（0.6831ν₀⁺T）；n₂σ为等于或低于2σ水平的实际循环数目（0.271ν₀⁺T）；n_3σ为等于或低于3σ水平的实际循环数目（0.0433ν₀⁺T）；N_1σ、N_2σ、N_3σ为根据疲劳曲线查得的1σ、2σ和3σ应力水平分别对应许可循环的次数。

利用1σ、2σ和3σ应力和统计平均频率计算随机疲劳是一个有效的过程。注意，统计平均频率等于载荷步4除以载荷步3结果的商。这样随机疲劳计算的一般过程是：

1）计算感兴趣应力分量的统计平均频率（应力速度/应力）。

2）假定68%的时间处于1σ水平，（95.73-68）27.45%的时间处于2σ水平，（99.73-95.45）4.33%的时间处于3σ水平。

3）基于期望（工作）寿命和统计平均频率，计算1σ，2σ和3σ水平下的循环次数。

4）基于S-N曲线计算疲劳寿命使用系数。

注意：上面所述只是为了说明如何利用ANSYS随机振动结果进行随机疲劳计算，仅仅介绍了部分应用途径，用户还可以根据其他随机振动疲劳计算理论进行计算，这里不一一罗列。在ANSYS中不能直接实现上述计算过程。