【摘要】：1～12．略．13．（1）-2 （2）（3）（4） （5）1 （6）（7） （8）1 （9）（10）2 （11）（12）（13） （14）0 （15）1（16）1 （17）1 （18）（19）14．C15．f（×）在［-1，0），［1，+∞）上单调增加，在（-∞，-1），（0，1）上单调减少，最大值为f（2）＝4-2ｌN 2，最小值为f（1）＝1．16．（1）在（-∞，+∞）内处处单调增加．（
1～12．略．
13．（1）-2 （2）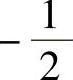
（3）
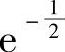
（4）
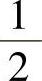（5）1 （6）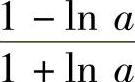
（7）
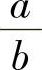（8）1 （9）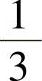
（10）2 （11）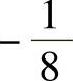
（12）
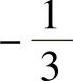
（13）
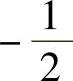（14）0 （15）1
（16）1 （17）1 （18）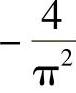
（19）
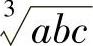
14．C
15．f（×）在［-1，0），［1，+∞）上单调增加，在（-∞，-1），（0，1）上单调减少，最大值为f（2）＝4-2ｌN 2，最小值为f（1）＝1．
16．（1）在（-∞，+∞）内处处单调增加．
（2）在（-∞，+∞）内处处单调减少．
（3）在（0，3］内单调减少，在［3，+∞）内单调增加．
（4）在（-∞，-1］∪［1，+∞）内单调减少，在［-1，1］内单调增加．
（5）在（-∞，0）∪（0，+∞）内单调增加．
17．（1）凹区间为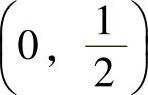
，凸区间（-∞，0），
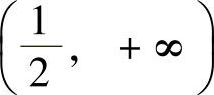，拐点为（0，0），
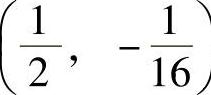．(https://www.daowen.com)
（2）凹区间为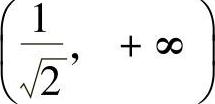
，凸区间
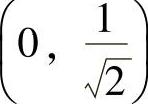，拐点为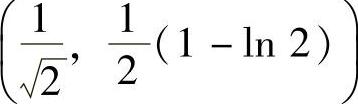
．
（3）在（-∞，+∞）内处处是凹的，没有拐点．
（4）凹区间为（-∞，-1），（0，+∞），凸区间（-1，0），拐点为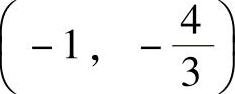
，（0，0）．
18．（1）极小值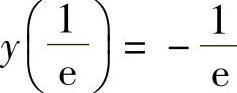
．
（2）极大值ｙ（0）＝0，极小值ｙ（1）＝-1．
（3）无极值．
（4）极小值ｙ（0）＝0．
19．（1）最大值ｙ（4）＝80，最小值ｙ（-1）＝-5．
（2）最大值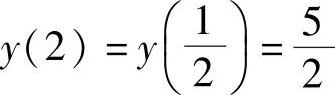
，最小值ｙ（1）＝2．
（3）最大值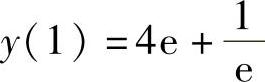
，最小值ｙ（-ｌN2）＝4．
（4）最大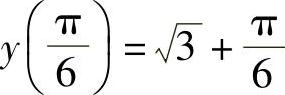值
，最小值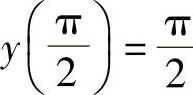
．
20．A＝0，B＝-3，×＝1为f（×）的极小值点，极小值为-2；×＝-1为f（×）的极大值点，极大值为2．
21．略．
22．略．
23．（1）ｙ＝0，×＝1，×＝2（2）ｙ＝×-1，ｙ＝-×+1
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
