1.用比较判别法判断下列级数的敛散性.
(1)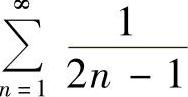 (2)
(2)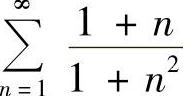
(3)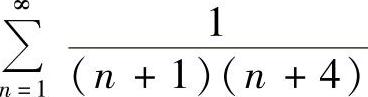 (4)
(4)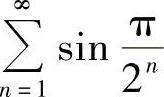
(5) (6)
(6)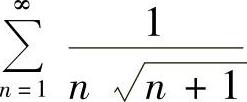
(7)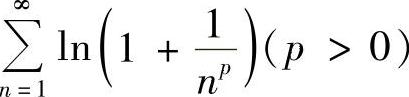 (8)
(8)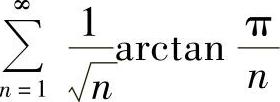
解 (1)因为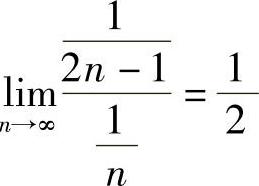 ,而
,而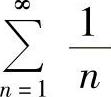 发散,由比较判别法知原级数发散.
发散,由比较判别法知原级数发散.
(2)由于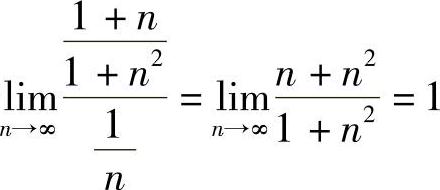 ,而
,而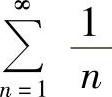 发散,由比较判别法知原级数发散.
发散,由比较判别法知原级数发散.
(3)由于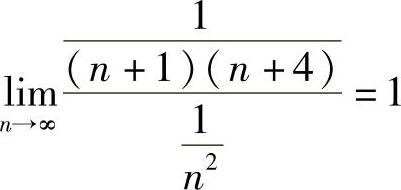 ,而
,而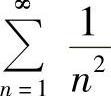 收敛,由比较判别法知原级数收敛.
收敛,由比较判别法知原级数收敛.
(4)由于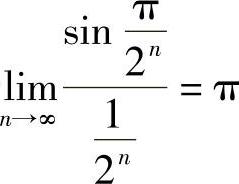 ,而
,而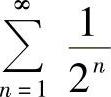 收敛,由比较判别法知原级数收敛.
收敛,由比较判别法知原级数收敛.
(5)由于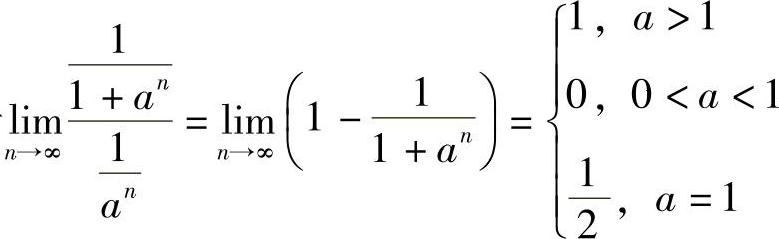 ,而
,而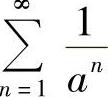 在A>1收敛,0<A≤1发散,所以原级数在A>1收敛,0<A≤1发散.
在A>1收敛,0<A≤1发散,所以原级数在A>1收敛,0<A≤1发散.
(6)由于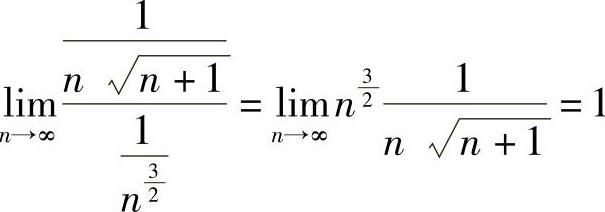 ,而
,而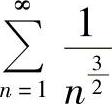 收敛,由比较判别法知原级数收敛.
收敛,由比较判别法知原级数收敛.
(7)由于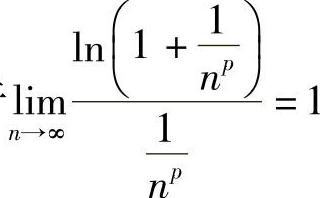 ,而
,而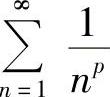 在P>1时收敛,在P≤1时发散,由比较判别法知原级数在P>1时收敛,在P≤1时发散.
在P>1时收敛,在P≤1时发散,由比较判别法知原级数在P>1时收敛,在P≤1时发散.
(8)由于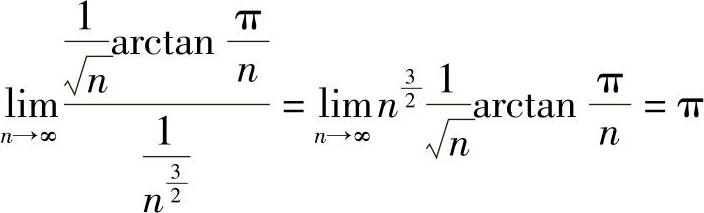 ,由比较判别法原级数收敛.
,由比较判别法原级数收敛.
2.用比值判别法判断下列级数的敛散性.
(1)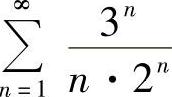 (2)
(2)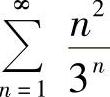
(3)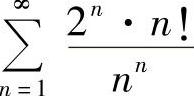 (4)
(4)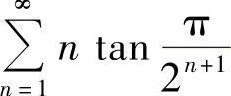
(5)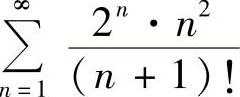 (6)
(6)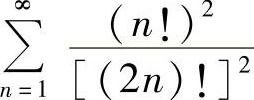
(7)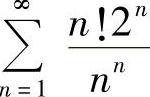 (8)
(8)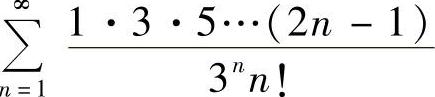
解 (1)由于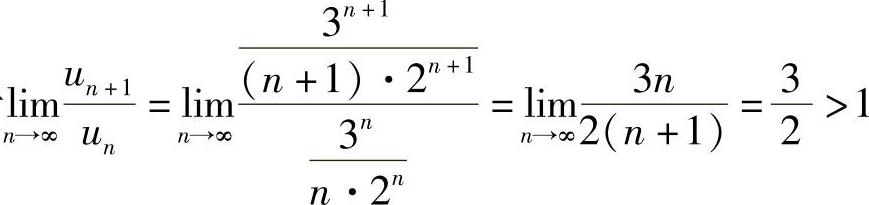 ,所以级数发散.
,所以级数发散.
(2)由于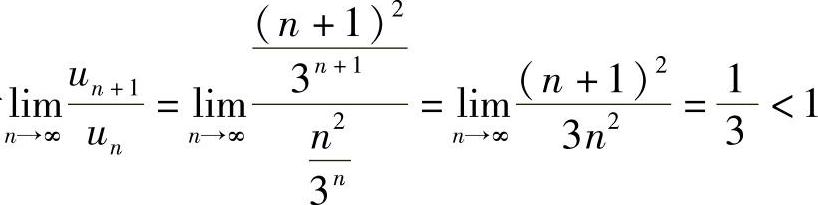 ,所以级数收敛.
,所以级数收敛.
(3)由于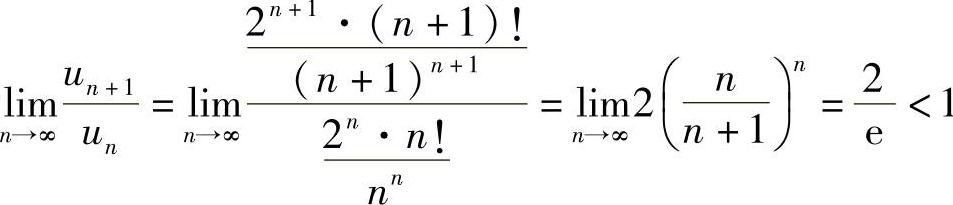 ,所以级数收敛.
,所以级数收敛.
(4)由于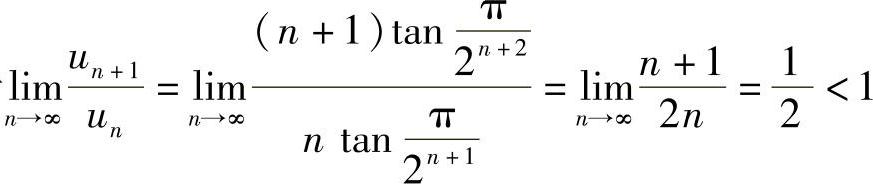 ,所以级数收敛.(www.daowen.com)
,所以级数收敛.(www.daowen.com)
(5)由于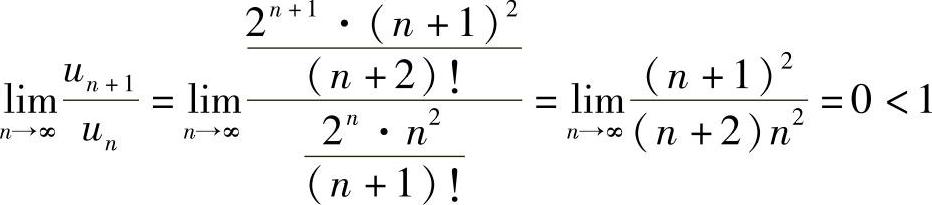 ,所以级数收敛.
,所以级数收敛.
(6)由于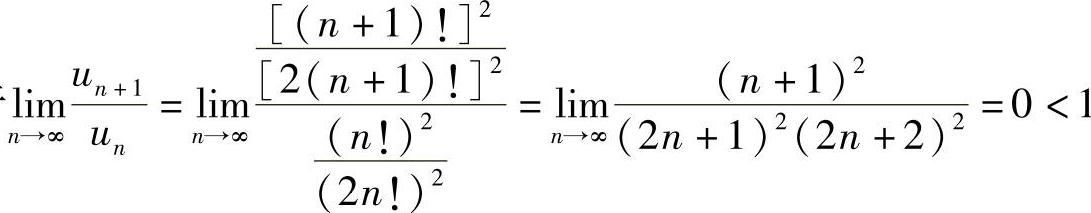 ,所以级数收敛.
,所以级数收敛.
(7)由于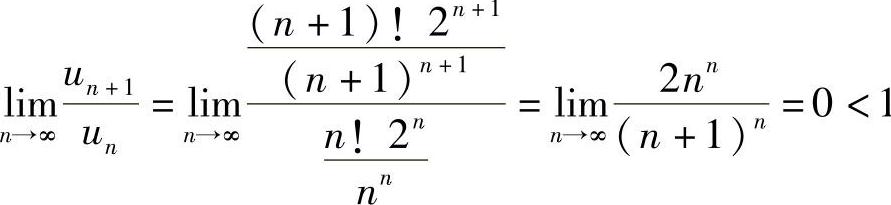 ,所以级数收敛.
,所以级数收敛.
(8)由于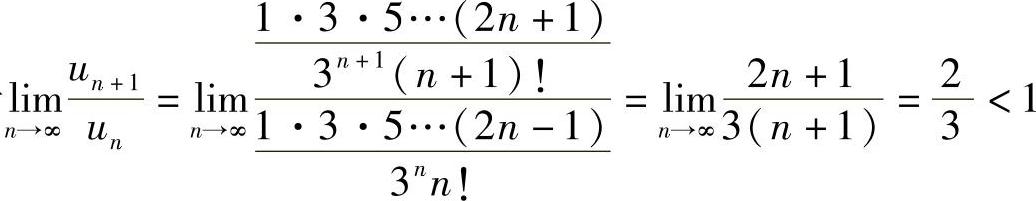 ,所以级数收敛.
,所以级数收敛.
3.用根值判别法判断下列级数的敛散性.
(1)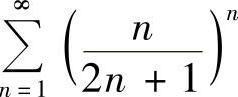 (2)
(2)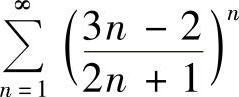
(3)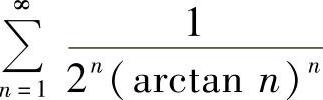 (4)
(4)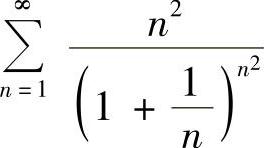
(5)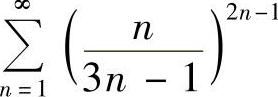 (6)
(6)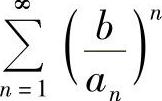 ,其中AN→A(N→∞),AN,B,A均为正数
,其中AN→A(N→∞),AN,B,A均为正数
解 (1)由于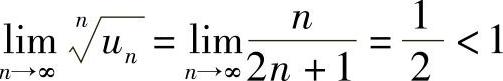 ,所以级数收敛.
,所以级数收敛.
(2)由于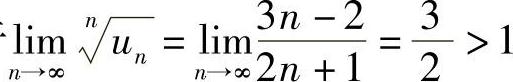 ,所以级数发散.
,所以级数发散.
(3)由于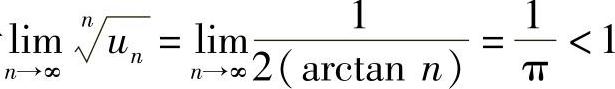 ,所以级数收敛.
,所以级数收敛.
(4)由于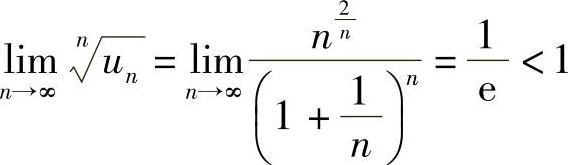 ,所以级数收敛.
,所以级数收敛.
(5)由于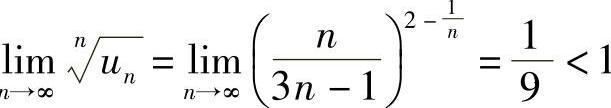 ,所以级数收敛.
,所以级数收敛.
(6)由于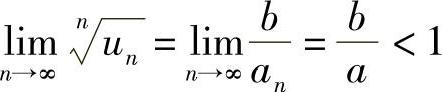 ,所以当B>A时级数发散,当B<A时级数收敛,A=B时,级数敛散性不定,不能用根值法判别.
,所以当B>A时级数发散,当B<A时级数收敛,A=B时,级数敛散性不定,不能用根值法判别.
4.设AN≤CN≤BN,(N=1,2,…),且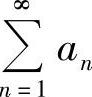 及
及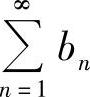 都收敛,证明级数
都收敛,证明级数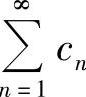 收敛.
收敛.
证 因为AN≤CN≤BN,所以BN-AN≥BN-CN>0,而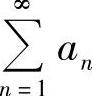 及
及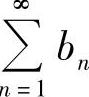 都收敛,所以级数
都收敛,所以级数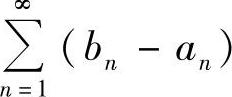 收敛,由比较判别法知
收敛,由比较判别法知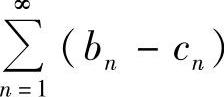 收敛,所以级数
收敛,所以级数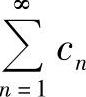 收敛.
收敛.
5.若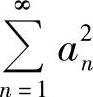 及
及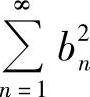 都收敛,证明下列级数都收敛.
都收敛,证明下列级数都收敛.
(1)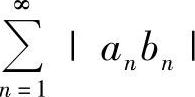 (2)
(2)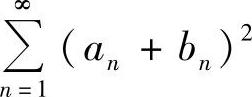 (3)
(3)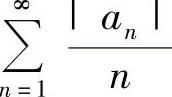
证(1)因为A2N+B2N≥2|AB|,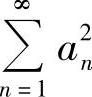 及
及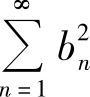 都收敛,
都收敛,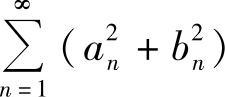 收敛,由比较判别法知
收敛,由比较判别法知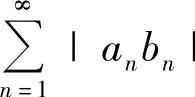 收敛.
收敛.
(2)因为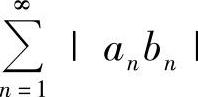 收敛,所以
收敛,所以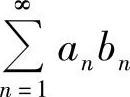 收敛,又由
收敛,又由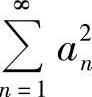 及
及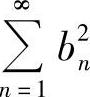 都收敛,故
都收敛,故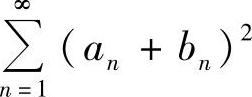 收敛.
收敛.
(3)因为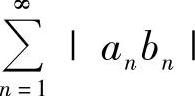 收敛,当
收敛,当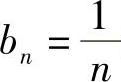 时,即
时,即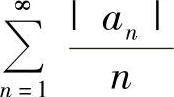 也收敛.
也收敛.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







