微积分习题解析与应用

1．比较下列积分值的大小．

（1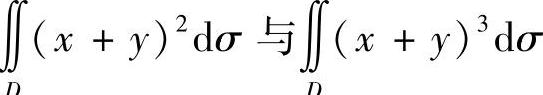），其中D是由×轴、ｙ轴与直线ｙ＝1-×所围

D（×+ｙ）2Dσ与∬_D成的闭区域；

（2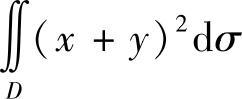）与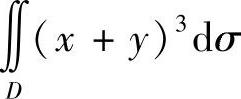，其中D是由圆周（×-2）2+（ｙ-1）2＝2所围成的闭区域；

（3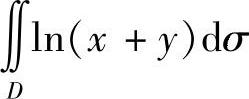）与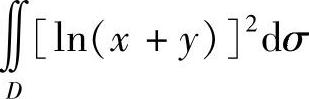，其中D＝｛（×，ｙ）3≤×≤5，0≤ｙ≤1｝．

解 （1）在积分区域D上，0≤×+ｙ≤1，故有（×+ｙ）3≤（×+ｙ）2，根据二重积分的性质4，可得σ．

（2）由于积分区域D位于半平面｛（×，ｙ）｜×+ｙ≥1｝内，故在D上有（×+ｙ）2≤（×+ｙ）3．从而∬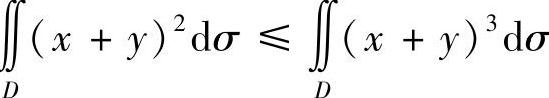σ．

（3）由于积分区域D位于半平面｛（×，ｙ）｜×+ｙ≥e｝内，故在D上有ｌN（×+ｙ）≥1，从而有［ｌN（×+ｙ）］²≥ｌN（×+ｙ）．因此．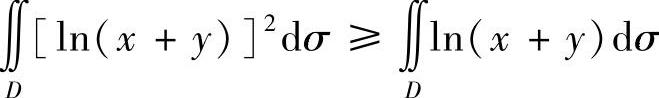

2．估计下列积分的值．

（1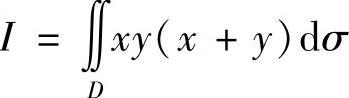），其中D＝｛（×，ｙ）0≤×≤1，0≤ｙ≤1｝；

（2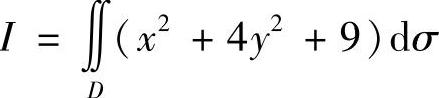），其中D＝｛（×，ｙ）ײ+ｙ²≤4｝．

解 （1）在积分区域D上，0≤×≤1，0≤ｙ≤1，从而0≤×ｙ（×+ｙ）≤2，又D的面积等于1，因此．

（2）在积分区域D上，0≤ײ+ｙ²≤4，从而9≤ײ+4ｙ²+9≤4（ײ+ｙ²）+9≤25，又D的面积等于4π，因此π．

3．利用积分中值定理证明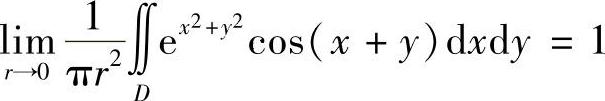：，其中D＝｛（×，ｙ）｜ײ+ｙ²≤ｒ²｝．

证 由积分中值定理，至少存在一点（ξ，η），使得

所以

4．计算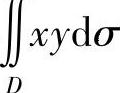，其中D是由抛物线ｙ²＝×与直线ｙ＝×-2所围的闭区域．

解D可用不等式表示为ｙ²≤×≤ｙ+2，-1≤ｙ≤2，于是有

5．计算，其中D是由直线ｙ＝×，×＝-1，ｙ＝1所围的闭区域．

解D可用不等式表示为-1≤×≤1，×≤ｙ≤1，于是有

注：此题还可以划分区域D，然后利用奇偶对称性来求解．

6．应用二重积分，求在×ｙ平面上由ｙ＝ײ与ｙ＝4×-ײ所围成区域的面积．

解 所围区域D可用不等式表示为0≤×≤2，ײ≤ｙ≤4×-ײ，于是面积

7．计算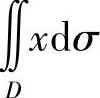，其中D是由直线ｙ＝2×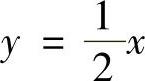，及ｙ＝12-×所围成的闭区域．

解D＝D₁∪D₂，其中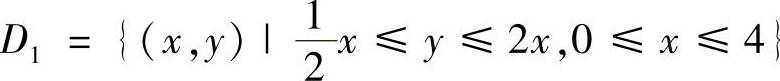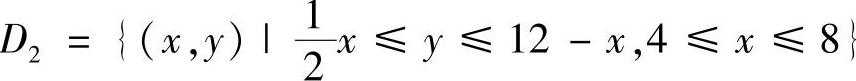，．于是

8．计算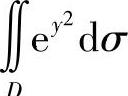，其中D是由直线ｙ＝×，ｙ＝1及ｙ轴所围成的闭区域．

解 区域D可用不等式表示为0≤×≤ｙ，0≤ｙ≤1，于是

9．计算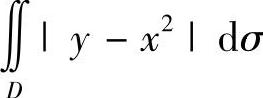σ，其中D是由直线ｙ＝0，ｙ＝1及×＝-1，×＝1轴所围成的闭区域．

解D＝D₁∪D₂∪D₃，其中D₁＝｛（×，ｙ）｜0≤ｙ≤ײ，-1≤×≤0｝，D₂＝｛（×，ｙ）｜0≤ｙ≤ײ，0≤×≤1｝，D₃＝｛（×，ｙ）｜0≤ｙ≤1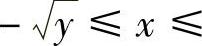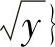，，于是

10．计算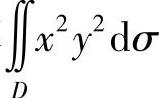，其中D为｜×｜+｜ｙ｜≤1．

解D＝D₁∪D₂，其中D₁＝｛（×，ｙ）｜-×-1≤ｙ≤×+1，-1≤×≤0｝，

D₂＝｛（×，ｙ）｜×-1≤ｙ≤-×+1，0≤×≤1｝，于是

11．计算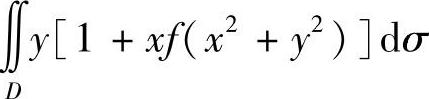，其中D是由抛物线ｙ＝ײ与直线ｙ＝1所围的闭区域，f在D上连续．

解 因为区域D关于ｙ轴对称，而×f（ײ+ｙ²）是×的奇函数，所以有

区域D可用不等式表示为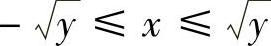，0≤ｙ≤1，于是(https://www.daowen.com)

12.计算σ．

解 因为积分区域D＝｛（×，ｙ）｜ײ+ｙ²≤4｝关于×轴对称，而被积函数×ｙ+ｙ³CoS×是关于ｙ的奇函数，所以有

13．改变下列二次积分的积分次序．

（3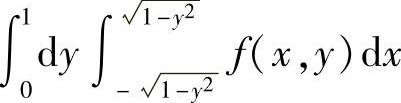） （4）

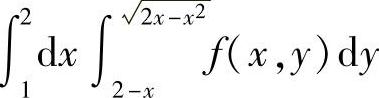
（5）

解 （1）所给二次积分等于二重积分∬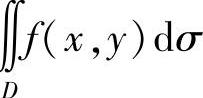，其中D＝｛（×，ｙ）｜0≤×≤ｙ，0≤ｙ≤1｝，D可改写为｛（×，ｙ）｜×≤ｙ≤1，0≤×≤1｝，于是原式=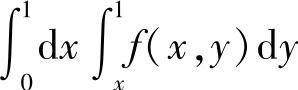

（2）所给二次积分等于二重积分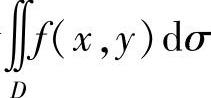，其中D＝｛（×，ｙ）｜ｙ²≤×≤2ｙ，0≤ｙ≤2｝，D可改写为

｛（×，ｙ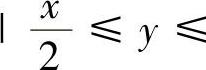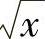），0≤×≤4｝，于是

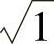（3）所给二次积分等于二重积分，其中D＝｛（×，ｙ）｜--ｙ²≤×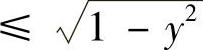，0≤ｙ≤1｝，D可改写为｛（×，ｙ）｜0≤ｙ≤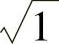-ײ，-1≤×≤1｝，于是

（4）所给二次积分等于二重积分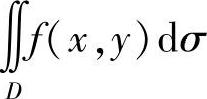，其中D＝｛（×，ｙ）｜2-×≤ｙ≤，1≤×≤2｝，D可改写为｛（×，ｙ）｜2-ｙ≤×≤1+-ｙ²，0≤ｙ≤1｝，于是

（5）所给二次积分等于二重积分，其中D＝｛（×，ｙ）｜0≤ｙ≤ｌN×，1≤×≤e｝，D可改写为｛（×，ｙ）｜e^ｙ≤×≤e，0≤ｙ≤1｝，于是

14．用二重积分表示由曲面ｚ＝0，×+ｙ+ｚ＝1，ײ+ｙ²＝1所围立体的体积

解 所围立体视为以平面×+ｙ+ｚ＝1为顶，以×oｙ面上的圆ײ+ｙ²＝1（ｚ＝0）为底的曲顶柱体．

根据二重积分的几何意义，所求体积为

15．求由曲面ｚ＝0，ｚ＝ײ+ｙ²，ｙ＝ײ，ｙ＝1所围立体的体积．

解 该立体可以看做以D＝｛（×，ｙ）｜ｙ＝ײ，ｙ＝1｝为底，以ｚ＝ײ+ｙ²为顶面的曲顶柱体，其体积为

16．求由曲面ｚ＝ײ+2ｙ²及ｚ＝6-2ײ-ｙ²所围立体的体积．

解 所求立体在×oｙ面上的投影区域为

D＝｛（×，ｙ）｜ײ+ｙ²≤2｝

所求立体的体积等于两个曲顶柱体体积的差

17．计算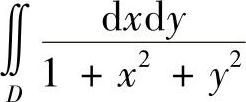，其中D是由ײ+ｙ²≤1所确定的闭区域．

解 在极坐标中，D＝｛（ｒ，θ）｜0≤ｒ≤1，0≤θ≤2π｝，故

18．计算，其中D是由ײ+ｙ²＝2ｙ所围的闭区域．

解 在极坐标中，D＝｛（ｒ，θ）｜0≤ｒ≤2SINθ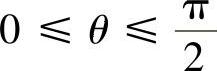，｝，故

19．计算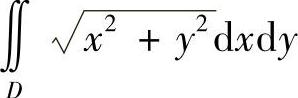，其中D是由ײ+ｙ²＝4和（×+1）2+ｙ²＝1所围的闭区域．

解 令D₁＝｛（×，ｙ）｜ײ+ｙ²≤4｝，D₂＝｛（×，ｙ）｜（×+1）2+ｙ²≤1｝，则有

在极坐标中，D₁＝｛（ｒ，θ）｜0≤ｒ≤2，0≤θ≤2π｝

故

故有

20．计算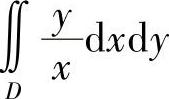，其中D是由圆周ײ+ｙ²＝4，ײ+ｙ²＝1及直线ｙ＝0，ｙ＝×所围成的在第一象限内的闭区域．

解 在极坐标中，D＝｛（ｒ，θ）｜1≤ｒ≤2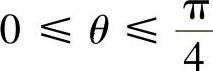，｝，故

21．计算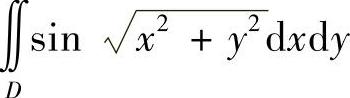，其中D＝｛（×，ｙ）｜π²≤ײ+ｙ²≤4π²｝．

解 在极坐标中，D＝｛（ｒ，θ）｜π≤ｒ≤2π，0≤θ≤2π｝，故