微积分：求解函数极值-微积分典型例题与解法

1．求下列函数的极值．

（1）ｚ＝ײ-×ｙ+ｙ²+9×-6ｙ+20；

（2）ｚ＝ײ+ｙ²-2ｌN×-2ｌNｙ；

（3）ｚ＝×ｙ（A-×-ｙ）（A≠0）．

解 （1）解方程组

求得驻点（-4，1）．

又A＝f_××（-4，1）＝2＞0，B＝f_×ｙ（-4，1）＝-1，C＝f_ｙｙ（-4，1）＝2，AC-B²＝3＞0．

由判定极值的充分条件知，在点（-4，1）处，函数取得极小值f（-4，1）＝-1．

（2）解方程组

求得驻点（1，1）．

又A＝f_××（1，1）＝4＞0，B＝f_×ｙ（1，1）＝0，C＝f_ｙｙ（1，1）＝4，AC-B²＝16＞0．

由判定极值的充分条件知，在点（1，1）处，函数取得极小值f（1，1）＝2．

（3）解方程组

求得驻点（0，0），（0，A），（A，0），.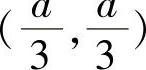

对于点（0，0），A＝f_××（0，0）＝0，B＝f_×ｙ（0，0）＝A，

C＝f_ｙｙ（0，0）＝0，AC-B²＝-A²＜0．

由判定极值的充分条件知，在点（0，0）处，函数不取得极值．对于点（0，A），A＝f_××（0，A）＝-2A，B＝f_×ｙ（0，A）＝-A，

C＝f_ｙｙ（0，A）＝0，AC-B²＝-A²＜0．

由判定极值的充分条件知，在点（0，A）处，函数不取得极值．对于点（A，0），A＝f_××（A，0）＝0，B＝f_×ｙ（A，0）＝-A，

C＝f_ｙｙ（A，0）＝-2A，AC-B²＝-A²＜0．

由判定极值的充分条件知，在点（A，0）处，函数不取得极值．

对于点，，，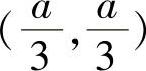

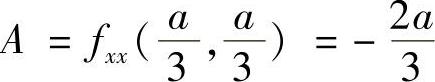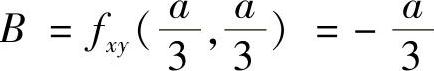由判定极值的充分条件知，在点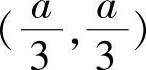处，当A＞0时，函数取得极大值；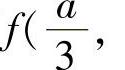

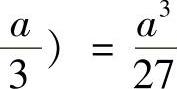当A＜0时，函数取得极小值．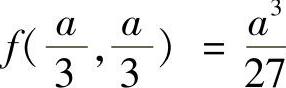

2．某工厂收入是以下两种可控决策量的函数：设×₁代表以千元为单位的用于存储的投资，×₂代表以千元为单位的用于广告的开支，则以千元为单位的收入为

Ｒ（×₁，×₂）＝-3ײ₁+2×₁×₂-6ײ₂+30×₁+24×₂-86

试问当存储投资和广告开支各为多少时收入额最大，最大收入额是多少？

解 因为Ｒ（×₁，×₂）＝-3ײ₁+2×₁×₂-6ײ₂+30×₁+24×₂-86，令

求解该方程组的×₁＝6，×₂＝3．由于驻点唯一，根据问题实际意义知最大值必存在，最大收入额为Ｌ（6，3）＝4万元．

3．某公司在生产中使用甲，乙两种原料，已知甲乙两种原料分别使用×单位和ｙ单位可生产Ｑ单位的产品，且

Ｑ＝Ｑ（×，ｙ）＝10×ｙ+20．2×+30．3ｙ-10ײ-5ｙ²

已知甲原料的单价为20元/单位，乙原料单价为30元/单位，产品每单位售价100元，产品固定成本1000元，求该公司的最大利润．

解 利润函数为Ｌ（×，ｙ）＝100·（10×ｙ+20．2×+30．3ｙ-10ײ-5ｙ²）-20×-

30ｙ-1000

＝1000（×ｙ+2×+3ｙ-ײ-0．5ｙ²-1）

令

求解该方程组的×＝5，ｙ＝8．由于驻点唯一，根据问题实际意义知最大值必存在．该公司的最大利润为Ｌ（5，8）＝16000．

4．求ｕ＝×ｙｚ在条件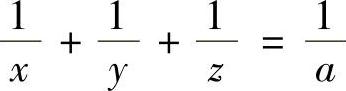（×，ｙ，ｚ，A为正数）下的极值．

解 作拉格朗日函数(https://www.daowen.com)

令

求解得×＝ｙ＝ｚ＝3A，由于驻点唯一，根据问题本身可知存在极小值为27A³．

5．旋转抛物面ｚ＝ײ+ｙ²被平面×+ｙ+ｚ＝1截成一椭圆，求这椭圆上的点到原点的距离的最大值和最小值．

解 设椭圆上的点为（×，ｙ，ｚ），则椭圆上的点到原点的距离的平方为

D²＝ײ+ｙ²+ｚ²

×，ｙ，ｚ满足条件ｚ＝ײ+ｙ²，×+ｙ+ｚ＝1．

作拉格朗日函数

Ｌ（×，ｙ，ｚ，λ，μ）＝ײ+ｙ²+ｚ²+λ（ｚ-ײ-ｙ²）+μ（×+ｙ+ｚ-1）

令

求解得，．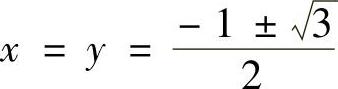

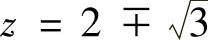于是得到两个可能的极值点，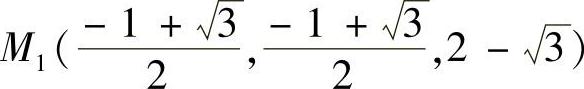

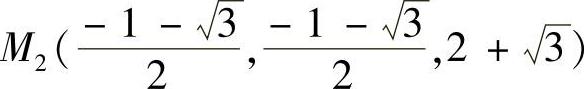
由题意可知这种距离的最大值和最小值一定存在，所以距离的最大值和最小值分别在这两点处取得．而

故最大值与最小值分别为

6．求表面积A²为而体积最大的长方体的体积．

解 设×，ｙ，ｚ分别为长方体的长、宽、高，则问题为在条件2（×ｙ+ｙｚ+×ｚ）＝A²下，求Ｖ＝×ｙｚ的最值．

作拉格朗日函数

Ｌ（×，ｙ，ｚ，λ，）＝×ｙｚ+λ［2（×ｙ+ｙｚ+×ｚ）-A²］

令

求解得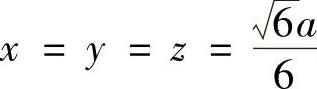．由于驻点唯一，根据问题本身可知存在最大值为．

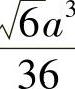7．设生产某种产品的产量Ｑ与所用两种原料甲、乙的数量×、ｙ间的函数关系是Ｑ＝Ｑ（×，ｙ）＝0．005ײｙ．欲用150万元资金购料，已知甲、乙原料的单价分别为1万元/吨和2万元/吨，问购进两种原料各多少时，可使生产的产品数量最多？

解 此问题为求×+2ｙ＝150的条件下，Ｑ＝Ｑ（×，ｙ）＝0．005ײｙ的最大值．

作拉格朗日函数Ｌ（×，ｙ）＝0．005ײｙ+λ（×+2ｙ-150）

令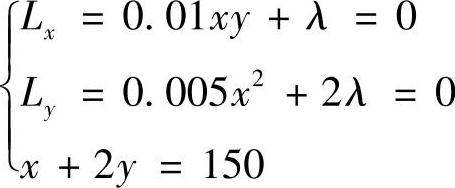

求解得×＝100，ｙ＝25，由于驻点唯一，根据问题实际意义知最大值必存在，生产的产品的量大数量为1250．

8．某公司通过电台及报纸两种方式做销售广告，收入Ｒ万元与电视广告费×万元及报纸广告费ｙ万元之间的关系为

Ｒ＝3（15+14×+32ｙ-8×ｙ-2ײ-10ｙ²）

利润额相当于三分之一的销售收益，并要扣除广告费用，试问在下列条件下，如何分配两种广告费用使得利润最大？（单位为万元）

（1）广告费用不限；

（2）提供的广告费用为1．5万元．

解 （1）利润函数为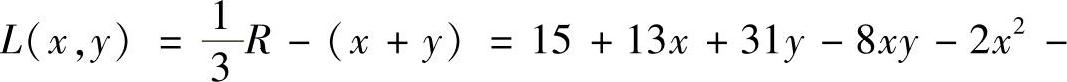10ｙ²

求函数Ｌ的各个偏导数，并令它们为0，得方程组

解得×＝0．75，ｙ＝1．25．则（0．75，1．25）为Ｌ（×，ｙ）唯一的驻点．

根据问题实际意义知最大值必存在，故最大值必在这唯一的驻点处达到．

因此，当电视广告费与报纸广告费分别为0．75万元和1．25万元时，最大利润为Ｌ（0．75，1．25）＝39．25万元．

（2）在×+ｙ＝1．5条件下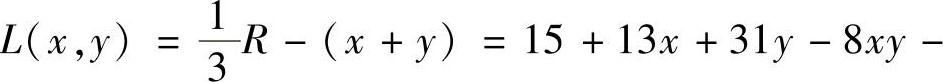，2ײ-10ｙ²的最大值．

作拉格朗日函数Ｌ（×，ｙ，λ）＝15+13×+31ｙ-8×ｙ-2ײ-10ｙ²+λ（×+ｙ-1．5）

令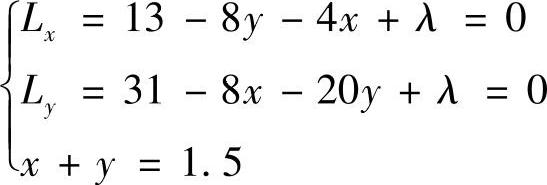

求解得×＝0，ｙ＝1．5，由于驻点唯一，根据问题实际意义知最大值必存在，因此，当电视广告费与报纸广告费分别为0万元和1．5万元时，最大利润为Ｌ（0，1．5）＝39万元．