1.求下列函数的偏导数.
(1)设z=euSINv,而u=×y,v=×+y,求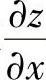 和
和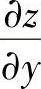 ;
;
(2)设u=f(×,y,z)=e×2+y2+z2,而z=×2SINy,求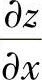 和
和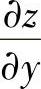 ;
;
(3)设z=uv,而u=×+2y,v=×-y,求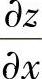 和
和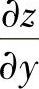 ;
;
(4)设u=f(×2-y2,e×y),求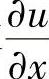 和
和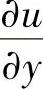 ;
;
(5)设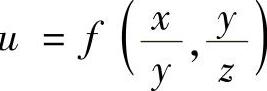 ,求
,求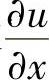 ,
,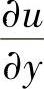 和
和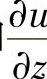 .
.
解 (1)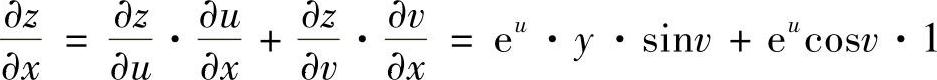
(2)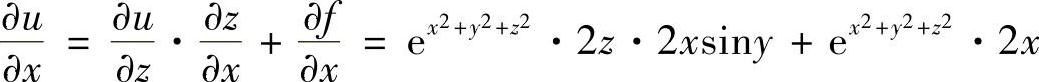
(3)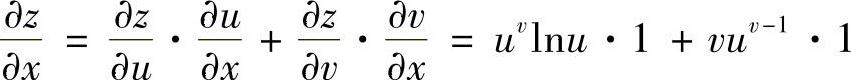
(4)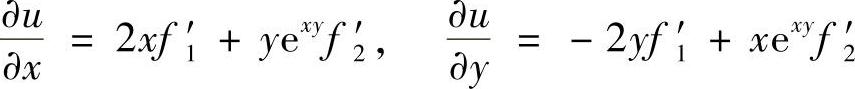
(5)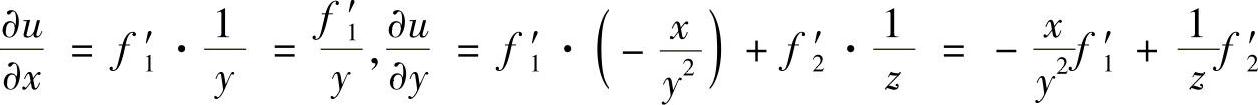
2.设z=f(×y,×2+y2),其中f具有二阶连续偏导数,求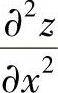 ,
,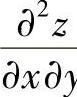 .
.
解 令S=×y,t=×2+y2,则z=f(×y,×2+y2),S和t是中间变量.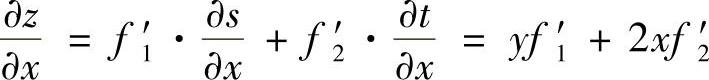 ,
,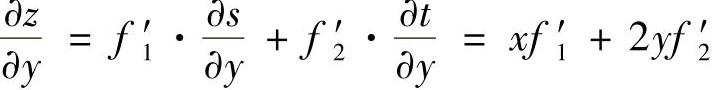
因为f(S,t)是S和t的函数,所以f′1和f2′也是S和t的函数,从而f′1和f2′是以S和t为中间变量的×和y的函数.故
3.设z=×y+×f(u),而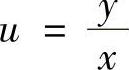 ,f(u)为可导函数,证明
,f(u)为可导函数,证明
证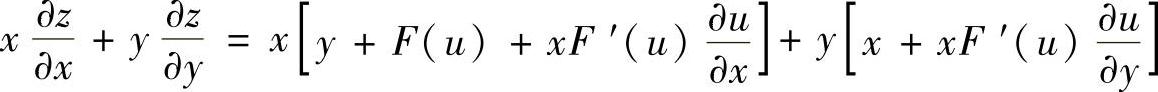
4.设z=f[e×y,CoS(×y)],f为可导函数,证明
证 令S=e×y,t=CoS(×y),则
所以有
5.设f(×,y)=f[×+g(y)],其中f具有二阶导数,g具有一阶导数,证明
证 令S=×+g(y),则有
而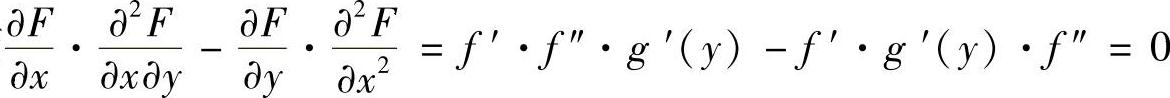 所以有
所以有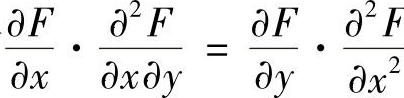 .(https://www.daowen.com)
.(https://www.daowen.com)
6.求下列方程所确定的隐函数的导数或偏导数.
(1)设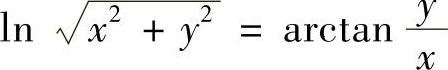 ,求
,求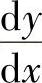 ;
;
(2)设ez-×yz=0,求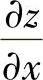 ,
,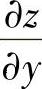 ;
;
(3)设×+y-z=×ez-y-×,求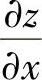 ,
,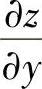 ;
;
(4)设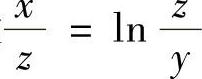 ,求
,求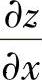 ,
,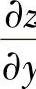 .y
.y
解 (1)设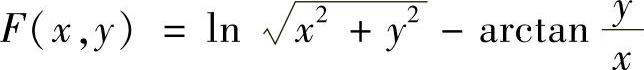 ,则
,则
(2)设f(×,y,z)=ez-×yz,则f×=-yz,fz=ez-×y,fy=-×z,
于是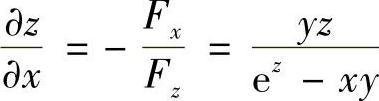 ,
,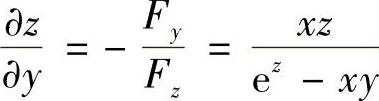
(3)f(×,y,z)=×ez-y-×-(×+y-z),则
f×=ez-y-×-×ez-y-×-1,fy=-×ez-y-×-1,fz=×ez-y-×+1
于是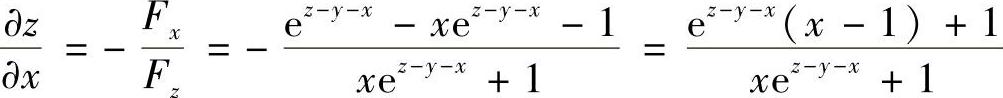
(4)令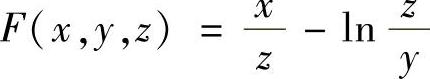 ,则
,则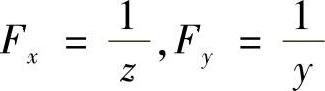 ,f
,f ,
,
于是
7.设u=f(×,y,z)有连续的偏导数,y=y(×)和z=z(×)分别由e×y-y=0和ez-×z=0所确定,求 .
.
解 令f(×,y)=e×y-y,则f×=ye×y,fy=×e×y-1,
令g(×,z)=ez-×z,则g×=-z,gz=ez-×,
所以
8.设f(u,v)具有连续偏导数,证明由方程f(C×-Az,Cy-Bz)=0所确定的函数z=f(×,y)满足 .
.
证 令u=C×-Az,v=Cy-Bz,则
于是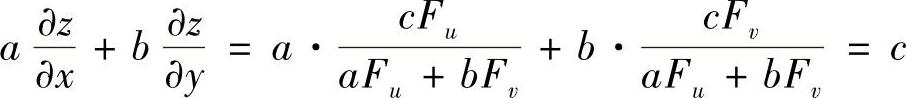
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






