微积分典型例题与解法-一阶偏导数求解与应用

1．求下列函数的一阶偏导数．

（1）ｚ＝׳ｙ-ｙ³× （2）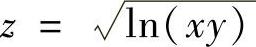

（3）ｚ＝SIN（×ｙ）+CoS²（×ｙ）

（4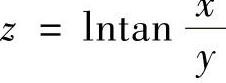）　（5）ｚ＝（1+×ｙ）ｙ （6）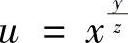

解 （1），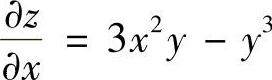

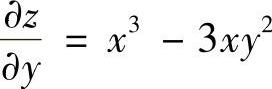
（2）

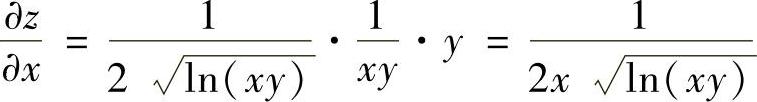
（3）

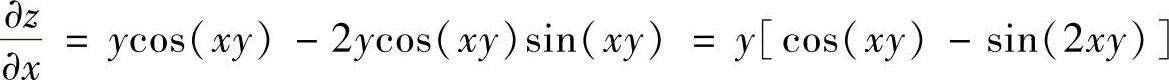
（4）

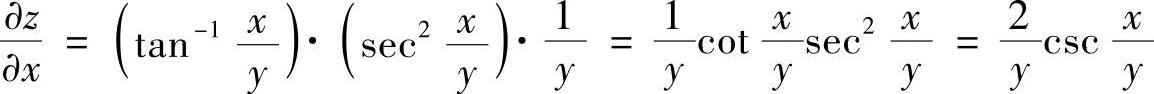
（5）

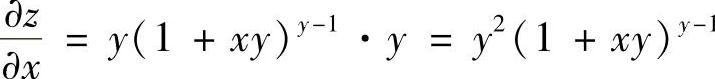
（6），，

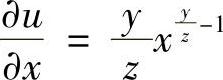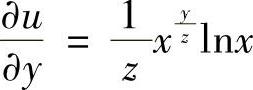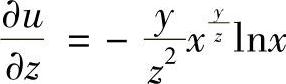
2．设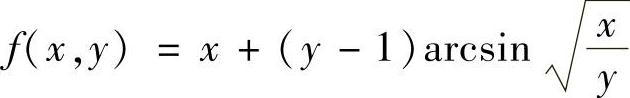，求f_×′（×，1）．

解 解法一 由于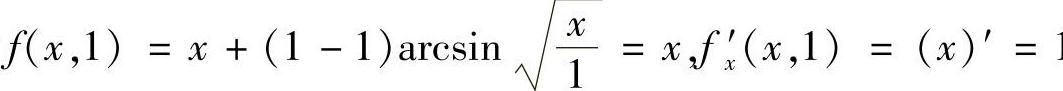

解法二．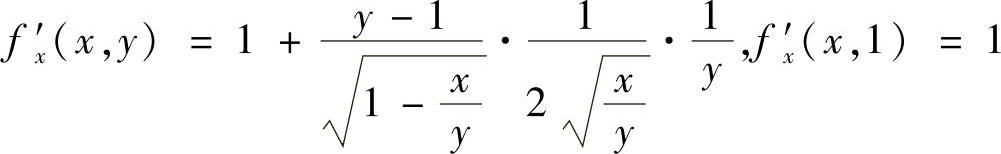

3．设f（×，ｙ）＝e^×2+ｙ2，求f_×′（1，1），f_ｙ′（1，0）．

解 解法一 由于f（×，1）＝e^×2+1，所以f_×′（×，1）＝e^×2+1·2×，f_×′（1，1）＝2e²．

由于f（1，ｙ）＝e^1+ｙ2，所以f_ｙ′（1，ｙ）＝e^1+ｙ2·2ｙ，f_ｙ′（1，0）＝0．

解法二f_×′（×，ｙ）＝e^×2+ｙ2·2×，f_ｙ′（×，ｙ）＝e^×2+ｙ2·2ｙ

f_×′（1，1）＝e¹⁺¹·2＝2e²，f_ｙ′（1，0）＝e¹⁺⁰·2·0＝0．

4．设ｚ＝×ｌN（×ｙ），求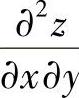．ｙ

解 因为，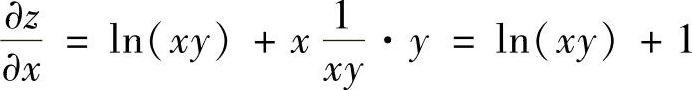

所以．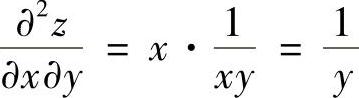

5．验证函数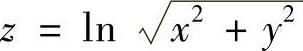满足方程．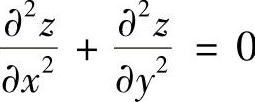

证 因为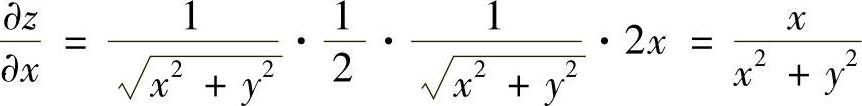，同理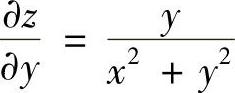，(https://www.daowen.com)

而，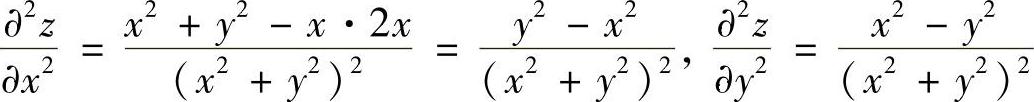

所以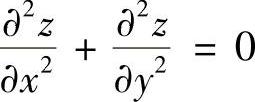

6．证明函数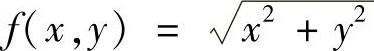在点（0，0）处偏导数不存在，但在该点连续．

证 因为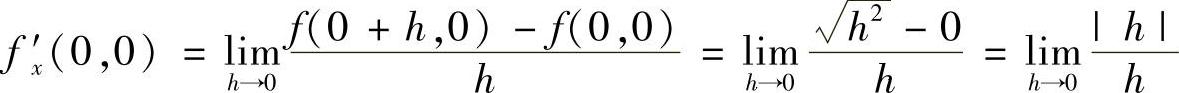，此极限不存在，所以函数在（0，0）处对×的偏导数不存在，同理函数在（0，0）处对ｙ的偏导数也不存在．

但是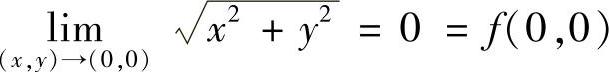，所以函数在该点连续．

7．考虑二元函数f（×，ｙ）的下面四条性质，说出它们之间的关系．

（1）f（×，ｙ）在点（×₀，ｙ₀）连续（2）f_×′（×，ｙ），f_ｙ′（×，ｙ）在点（×₀，ｙ₀）连续

（3）f（×，ｙ）在点（×₀，ｙ₀）可微（4）f_×′（×，ｙ），f_ｙ′（×，ｙ）在点（×₀，ｙ₀）存在

解 由于二元函数偏导数存在且连续是二元函数可微分的充分条件，二元函数可微分必定可（偏）导，二元函数可微分必定连续．因此（2）⇒（3）⇒（1）．

8．求下列函数的全微分．

（1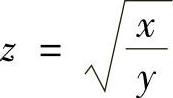）　（2）ｕ＝×ｙｚ

解 （1），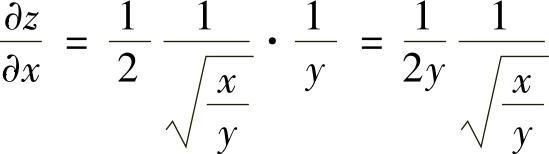

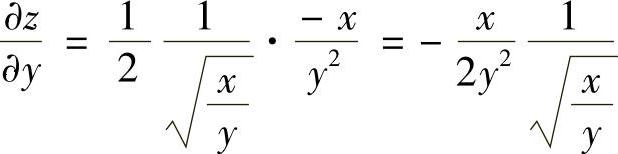
（2），，

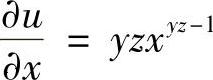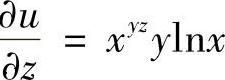
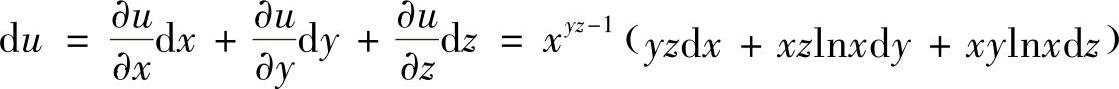
9．求函数ｚ＝ｌN（1+ײ+ｙ²）在×＝1，ｙ＝2，Δ×＝0．1，Δｙ＝-0．1时的全微分．

解 因为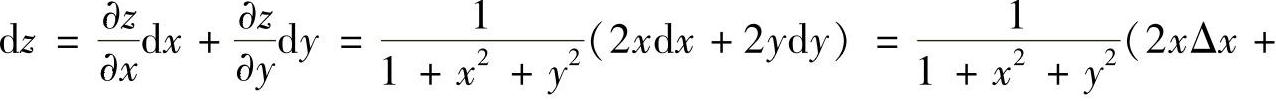

2ｙΔｙ），

所以当×＝1，ｙ＝2，Δ×＝0．1，Δｙ＝-0．1时全微分为

10．已知边长为×＝6m与ｙ＝8m的矩形，如果×边增加5Cm而ｙ边减少10Cm，此矩形对角线变化的近似值．

解 矩形的对角线的长为，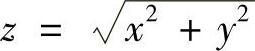

当×＝6，ｙ＝8，Δ×＝0．05，Δｙ＝-0．1时，

即这个矩形的对角线的长减少大约5Cm．