【摘要】:1.求下列各函数的定义域.(1) (2) (3)(4) (5) (6)解 (1)定义域为{(×,y)×≥0,-∞<y<+∞};(2)定义域为{(×,y)|×|≤1,|y|≥1};(3)定义域为{(×,y)|×2+y2≠0};(4)定义域为{(×,y)|y≥0,×≥y};(5)定义域为{(×,y)|×2+y2≤1,y>×2};(6)定义域为{(×,y)|×+y>0,×-y>0}.注 本题时求多元函数
1.求下列各函数的定义域.
(1)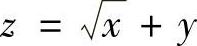 (2)
(2)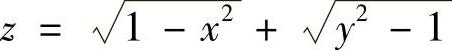 (3)
(3)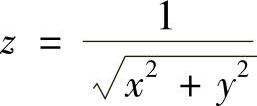
(4)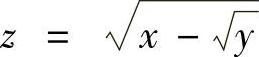 (5)
(5)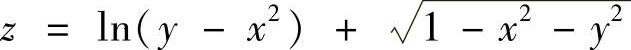 (6)
(6)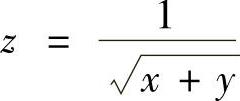
解 (1)定义域为{(×,y)×≥0,-∞<y<+∞};
(2)定义域为{(×,y)|×|≤1,|y|≥1};
(3)定义域为{(×,y)|×2+y2≠0};
(4)定义域为{(×,y)|y≥0,×≥y};
(5)定义域为{(×,y)|×2+y2≤1,y>×2};
(6)定义域为{(×,y)|×+y>0,×-y>0}.
注 本题时求多元函数的定义域,与求一元函数的定义域相类似,先写出构成该函数的各个简单函数的定义域,再求出表示这些定义域的集合的交集,即得所求定义域.
2.(1)已知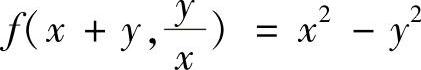 ,求f(×,y);
,求f(×,y);
(2)已知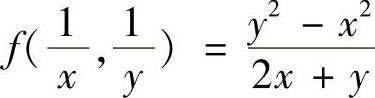 ,求f(×,y).
,求f(×,y).
解 (1)令u=×+y,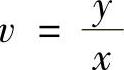 ,则
,则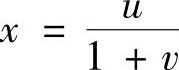 ,
,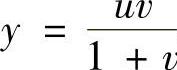 .
.
故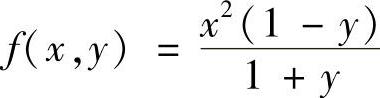 .
.
(2)因为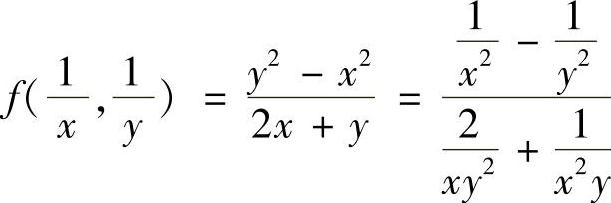 ,则
,则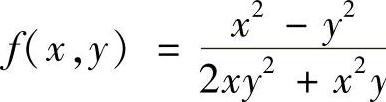 .
.
3.设f(×+y,×-y)=e×2+y2(×2-y2),求f(×,y)和f(2,2)的值.(https://www.daowen.com)
解 因为f(×+y,×-y)=e×2+y2(×2-y2)
所以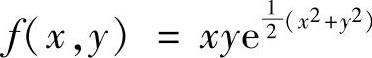 ,
,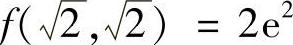 .
.
4.设z=×+y+f(×-y),且当y=0时,z=×2,求函数z的表达式.
解 因为当y=0时,z=×2,即×+f(×)=×2,则有
f(×)=×2-×,f(×-y)=(×-y)2-(×-y)
故z=(×-y)2+2y.
5.求下列各极限.
(1)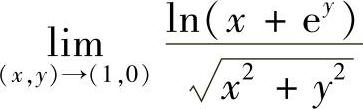
(2)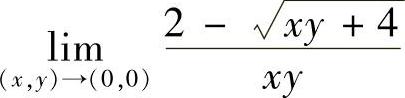
(3)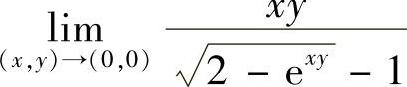
(4)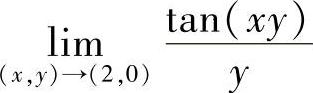
解 (1)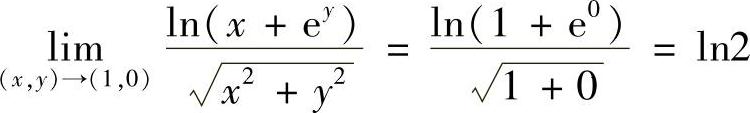
(2)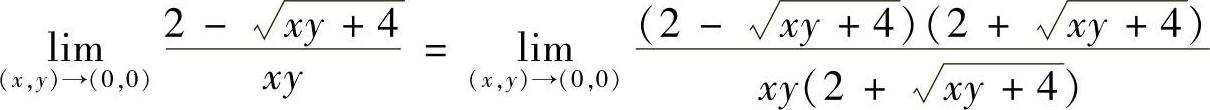
(3)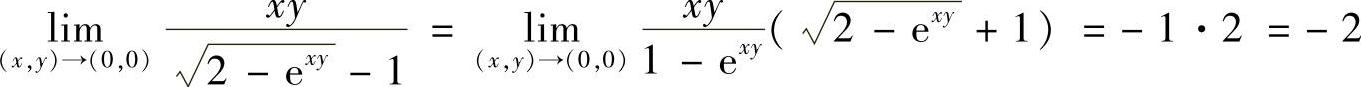
(4)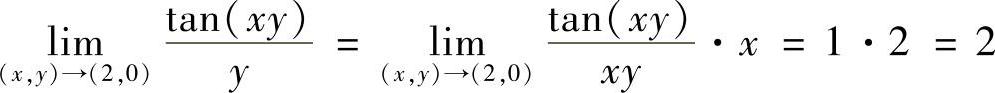
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章





