1.在空间坐标系下,指出下列各点所在的卦限.
A.(1,-2,3) B.(2,3,-4) C.(2,-2,-3) D.(-1,-2,3)
解 A点在第四卦限;B点在第五卦限;C点在第八卦限;D点在第三卦限.
2.坐标面和坐标轴上的点有何特征?指出下列各点的位置.
A.(1,2,0) B.(0,3,-4) C.(2,0,0) D.(0,-2,0)
解 在坐标面上点的坐标,其特征是表示坐标的三个有序数中至少有一个为零,比如在×oy面上的点的坐标为(×0,y0,0),×oz面上的点的坐标为(×0,0,z0),yoz面上的点的坐标为(0,y0,z0).
在坐标轴上点的坐标,其特征是表示坐标的三个有序数中至少有两个为零,比如在o×轴上的点的坐标为(×0,0,0),oz面点的点的坐标为(0,0,z0),oy面点的点的坐标为(0,y0,0).
因此,A点在×oy面上;B点在yoz面上;C点在×轴上;D点在y轴上.
3.一动点到两定点(2,3,1)和(1,2,5)的距离相等,求动点的轨迹方程.
解 设动点为m(×,y,z),由题意知
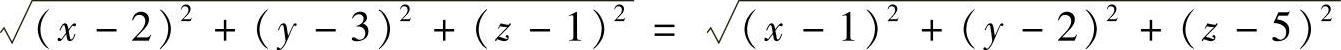
经整理得×+y-4z+8=0.
4.求以点P(1,3,-2)为球心且通过坐标原点的球面方程.
解 设球面上的任意一点为(×,y,z),由题意知
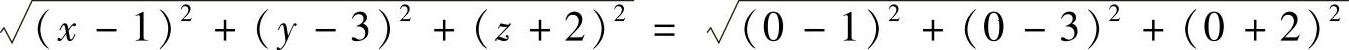
经整理得×2+y2+z2-2×-6y+4z=0.
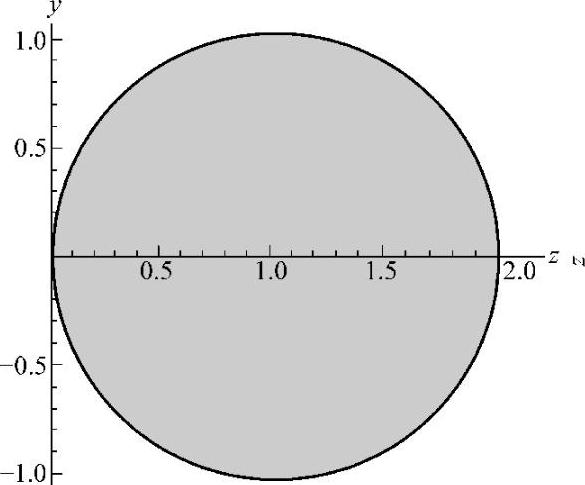
5.画出下列各方程所表示的曲面.
(1)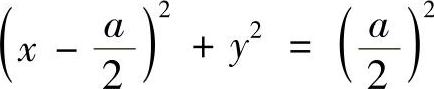 (2)z=2-×2 (3)
(2)z=2-×2 (3)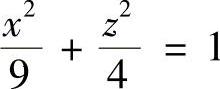
解(1)如图7⁃5A;(2)如图7⁃5B;(3)如图7⁃5C.
 (https://www.daowen.com)
(https://www.daowen.com)
图 7⁃5A
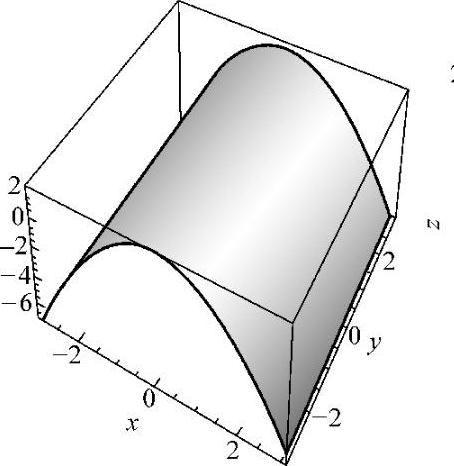
图 7⁃5B
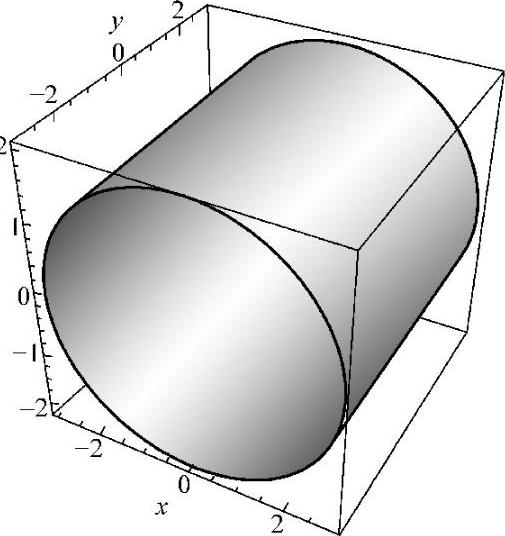
图 7⁃5C
6.指出下列各方程表示何种曲面.
(1)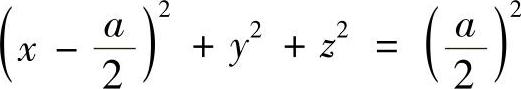 (2)z=×2+y2(3)
(2)z=×2+y2(3)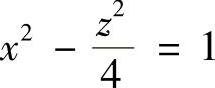
(4)×2=4y(5)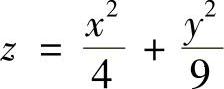 (6)
(6)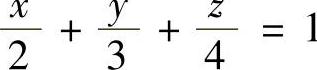
解 (1)表示以 为中心,半径为
为中心,半径为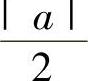 的球面;
的球面;
(2)旋转抛物面;
(3)双曲柱面;
(4)抛物柱面;
(5)椭圆抛物面;
(6)平面;
7.判定下列平面点集中哪些是开集,闭集,区域,有界集,无界集.
(1){(×,y)|×≠0,y≠0}(2){(×,y)|1<×2+y2≤4}(3){(×,y)|y>×2}
解(1)集合是开集,无界集;
(2)集合既非开集,又非闭集,是有界集;
(3)集合是开集,区域,无界集.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







