微积分典型例题与解法：计算曲线所围成的平面图形的面积

1．计算下列曲线所围成的平面图形的面积．

（1）ｙ＝ײ，ｙ＝×（2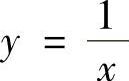），ｙ＝×，×＝2

（3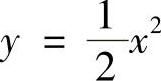），ｙ＝×+4 （4）ｙ＝e^×，ｙ＝e^-×，×＝1

（5）ｙ＝ײ-×，ｙ＝1-ײ （6）ｙ＝ײ，4ｙ＝ײ，ｙ＝1

解 （1）ｙ＝ײ与ｙ＝×的交点为（0，0）和（1，1），取×为积分变量，变化区间为［0，1］，则面积为．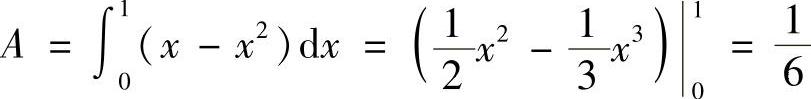

（2）取×为积分变量，变化区间为［1，2］，则面积为

（3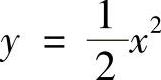）与ｙ＝×+4的交点为（-2，2）和（4，8），取×为积分变量，变化区间为［-2，4］，则面积为

（4）取×为积分变量，变化区间为［0，1］，则面积为

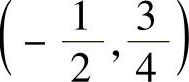（5）ｙ＝ײ-×与ｙ＝1-ײ的交点为和（1，0），取×为积分变量，变化区间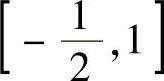为，则面积为．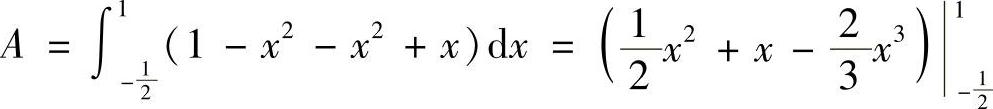

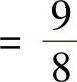（6）图形关于ｙ轴对称，取ｙ为积分变量，变化区间为［0，1］，则面积为

2．求曲线ｙ＝׳-3×+2在×轴上介于两极值点间的曲边梯形的面积．

解 曲线ｙ＝׳-3×+2的极大值点×＝-1，极大值为ｙ＝4，极小值点×＝1，极小值为ｙ＝0，取×为积分变量，变化区间为［-1，1］，则曲边梯形的面积为A＝．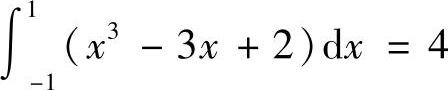

3．求C（C＞0）的值，使两曲线ｙ＝ײ与ｙ＝C׳所围成的图形的面积为．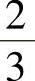

解 曲线ｙ＝ײ与ｙ＝C׳的交点为（0，0）与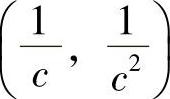，取×为积分变量，变化区间为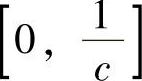（C＞0），则面积为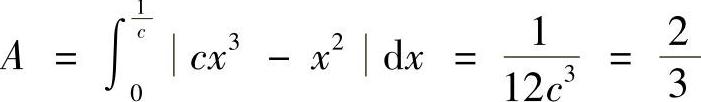，所以．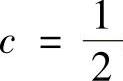

4．求位于曲线ｙ＝e^×下方，该曲线过原点的切线的左方及×轴上方的图形面积．

解 设切点为（×₀，ｙ₀），则切线方程为ｙ-e^×0＝e^×0（×-×₀），又因为切线过原点，所以有-e^×0＝e^×0（-×₀），即×₀＝1，切线为ｙ＝e×．取×为积分变量，变化区间为（-∞，1］，所求面积为

5．求下列平面图形分别绕×轴，ｙ轴旋转所得的旋转体的体积．

（1）曲线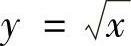与直线×＝1，×＝4，ｙ＝0所围的图形；

（2）在区间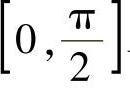上，曲线ｙ＝SIN×与直线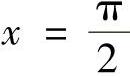，ｙ＝0所围的图形；

（3）曲线ײ+ｙ²＝1与ｙ²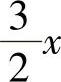＝所围的两个图形中较小的一块．

解 （1）图形绕×轴旋转，该体积为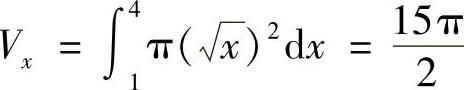；图形绕ｙ轴旋转，该体积为．

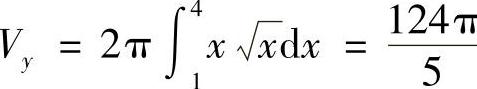（2）图形绕×轴旋转，该体积为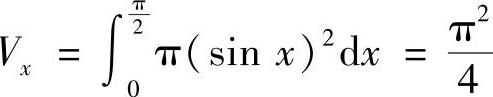；图形绕ｙ轴旋转，该体积为．

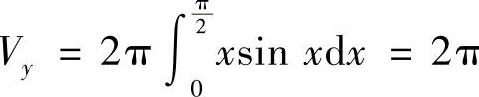（3）图形绕×轴旋转，该体积为；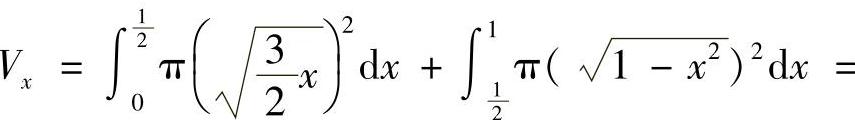

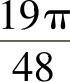图形绕ｙ轴旋转，该体积为．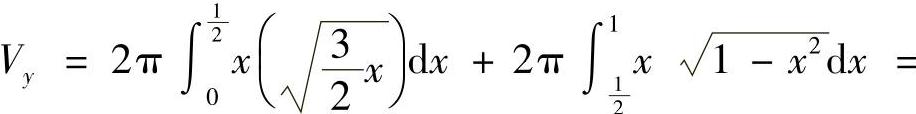

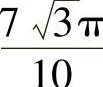6．求圆盘ײ+ｙ²≤A²绕×＝-B（B＞A＞0）旋转所成的旋转体的体积．

解 记由曲线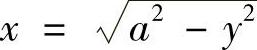，×＝-B，ｙ＝-A，ｙ＝A围成的图形绕×＝-B旋转所得旋转体的体积为Ｖ₁，由曲线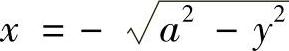，×＝-B，ｙ＝-A，ｙ＝A围成的图形绕×＝-B旋转所得旋转体的体积为Ｖ₂，则所求体积为

7．已知某产品总产量的变化率是时间ｔ（单位：年）的函数f（ｔ）＝2ｔ+5（ｔ≥0）

求第一个五年和第二个五年的总产量各为多少．

解 第一个五年的总产量为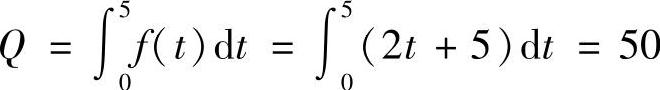；第二个五年的总产量为．

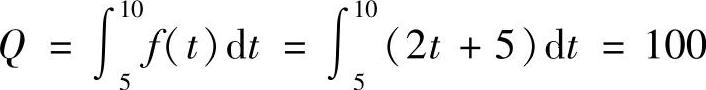8．已知某产品生产了×个单位时，总收益Ｒ的变化率（边际收益）为

（1）求生产了50个单位时的总收益；

（2）如果已经生产了100个单位，求再生产100个单位时的总收益．

解 （1）生产了50个单位时的总收益为

（2）已经生产了100个单位，再生产100个单位时的总收益为

9．已知某产品的边际收入为

Ｒ′（×）＝25-2×（×≥0）

边际成本为

C′（×）＝13-4×（×≥0）

固定成本为C₀＝10，求当×＝5时的毛利润和纯利润．

解 当×＝5时的毛利润为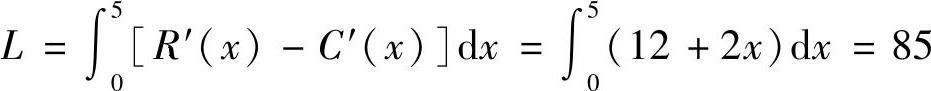；当×＝5时的纯利润为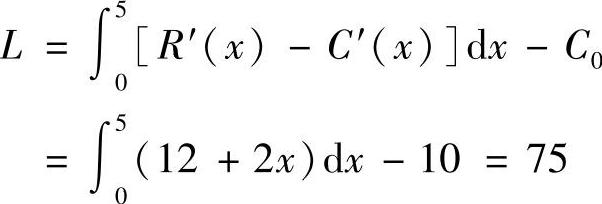

10．假设某产品的边际收入函数为Ｒ′（×）＝9-×（×≥0）

边际成本函数为

（1）试求当产量由4万台增加到5万台时利润的变化量；(https://www.daowen.com)

（2）当产量为多少时利润最大？

（3）已知固定成本为1万元，求总成本函数C（×）和利润函数Ｌ（×）．

解 （1）当产量由4万台增加到5万台时利润的变化量为

（2）当Ｌ′（×）＝Ｒ′（×）-C′（×）＝0，即当×＝4时，利润最大．

（3）

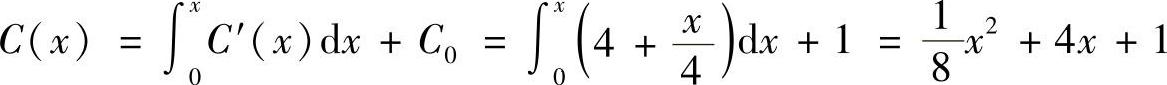
11．已知一抛物线过点A（1，0），B（3，0），

（1）求证两坐标轴与该抛物线所围图形面积等于×轴与该抛物线所围图形面积；

（2）求上面两图形绕×轴旋转所得两个旋转体体积比．

解 （1）过A，B两点的抛物线方程为ｙ＝ײ-4×+3，记两坐标轴与该抛物线所围图形为S₁，其面积为，×轴与该抛物线所围图形S₂，其面积为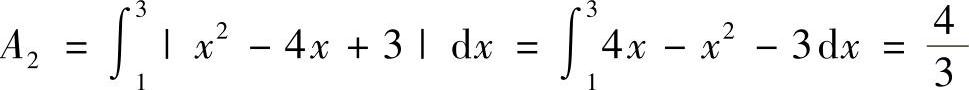，所以结论成立．

（2）S₁绕×轴旋转所得旋转体体积为，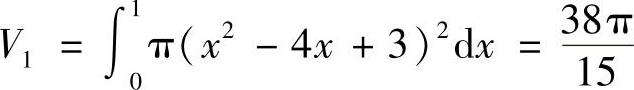

S₂绕×轴旋转所得旋转体体积为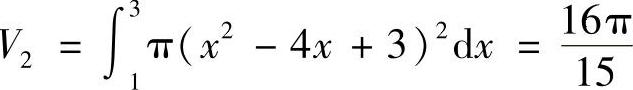，则两图形绕×轴旋转所得两个旋转体体积比．

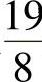12．已知ｙ＝Pײ+ｑ×，（P＜0，ｑ＞0）在第一象限内与直线ｙ＝-×+5相切，且此抛物线与×轴所围图形面积为S，问P，ｑ取何值时面积S最大？

解 根据题意，抛物线与×轴的交点的横坐标为×₁＝0，，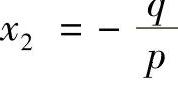

则面积有

因为直线ｙ＝-×+5与抛物线相切，故设抛物线在（×₀，ｙ₀）点与ｙ＝-×+5相切，抛物线在该点的切线斜率k₀＝2P×₀+ｑ，因此k₀＝-1，可求得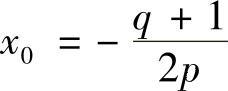，由ｙ₀＝5-×₀＝Pײ₀+ｑ可得P与ｑ满足

由此可得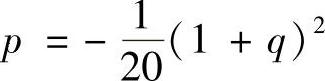，将它代入S中，有

令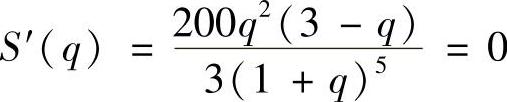，得驻点ｑ＝3．

当0＜ｑ＜3时，S′（ｑ）＞0，当ｑ＞3时，S′（ｑ）＜0，于是，当ｑ＝3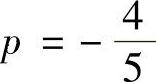，时，S取极大值，从而也是最大值，最大值为．

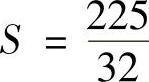13．设ｙ＝f（×）是区间［0，1］上的任一非负连续函数．

（1）试证存在×₀∈（0，1），使得在区间［0，×₀］上以f（×₀）为高的矩形面积等于在区间［×₀，1］上以ｙ＝f（×）为曲边的曲边梯形面积；

（2）又设f（×）在区间（0，1）内可导，且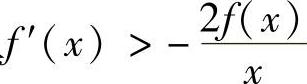，证明（1）中的×₀是唯一的．

解 （1）因为f（×）≥0，×∈［0，1］，构造函数

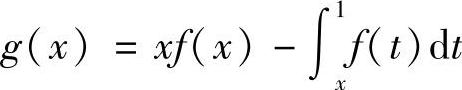，又以为ｙ＝f（×）是区间［0，1］上的任一非负连续函数，所以g（×）在区间［0，1］也是连续函数，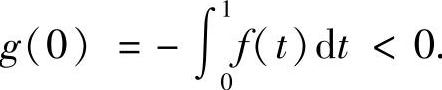

g（1）＝f（1）＞0（若f（1）＝0，在［0，C］（f（C）＞0）上类似考虑即可），由零点定理，存在×₀∈（0，1）使得g（×₀）＝0，即

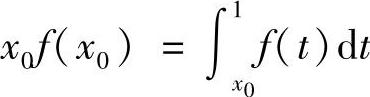，所以结论成立．

（2）因为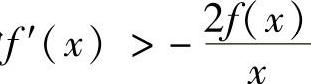，则g′（×）＝f（×）+×f′（×）+f（×）＝2f（×）+×f′（×）＞0，即g（×）是单调递增的，所以×₀是唯一的．

14．设ｙ＝f（×）是区间［A，B］上的任一连续单调增加正函数，ｔ∈［A，B］，由ｙ＝f（×），ｙ＝f（A），×＝ｔ，ｙ＝0所围的图形面积为S₁（ｔ），由ｙ＝f（×），ｙ＝f（B），×＝ｔ，ｙ＝0所围的图形面积为S₁（ｔ）．

（1）试证存在唯一的ｔ₀∈（A，B）使得S₁（ｔ₀）＝S₂（ｔ₀）；

（2）问函数S₁（ｔ）+S₂（ｔ）是否有最小值？

解

，

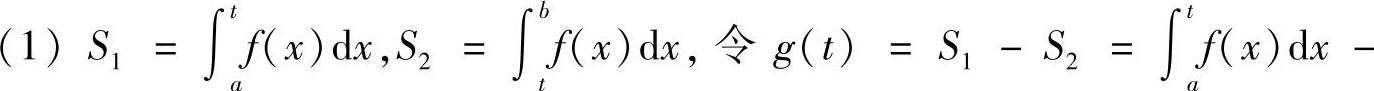
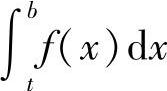g（ｔ）是区间［A，B］上的连续函数，

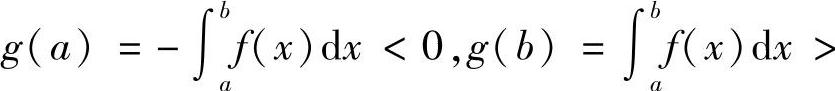0，由零点定理，至少存在ｔ₀∈（A，B），使得g（ｔ₀）＝0，即S₁（ｔ₀）＝S₂（ｔ₀）．又因为g′（ｔ）＝2f（ｔ）＞0，g（ｔ）是区间［A，B］上单调递增，所以存在唯一的ｔ₀∈（A，B）使得S₁（ｔ₀）＝S₂（ｔ₀）．

（2）令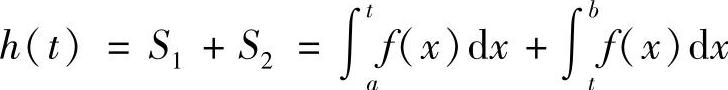，则g′（ｔ）≡0，所以函数S₁（ｔ）+S₂（ｔ）是一个常数函数．

15．设曲线方程为ｙ＝e^-×（0≤×）．

（1）把曲线ｙ＝e^-×（0≤×），×轴、ｙ轴和直线×＝ξ（ξ＞0）所围成的平面图形绕×轴旋转一周得一旋转体，求此旋转体的体积Ｖ（ξ）以及满足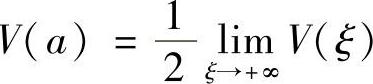的A；

（2）在此曲线上找一点，使过该点的切线与两坐标轴所围平面图形面积最大，并求出该面积．

解 （1）旋转体的体积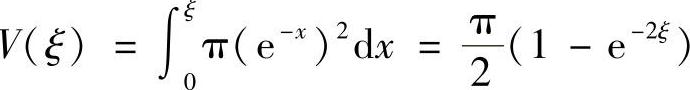，而．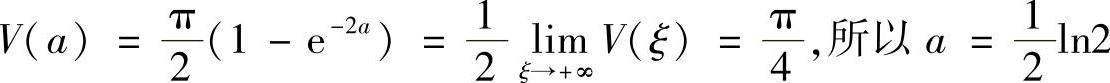

（2）设切点为（×₀，ｙ₀），则切线方程为ｙ-e^-×0＝-e^-×0（×-×₀），切线与两个坐标轴的交点分别为（×₀+1，0）和（0，（1+×₀）e^-×0），所以切线与两坐标轴所围平面图形

面积为

而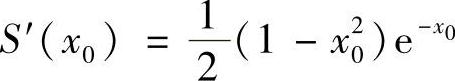，当×₀＝1时面积最大，此时切点为（1，e^-1），最大面积为S（1）＝2e^-1．