【摘要】:1.用换元法计算下列各定积分.(1) (2)(3) (4)(5) (6)解 (1)(2)(3)(4)(5)(6)2.用分部积分计算下列各定积分.(1) (2)(3)(4) (5)解(1)(2)因此有.(3)(4)(5)3.利用函数奇偶性计算下列各定积分.(1) (2)(3) (4)(5)解 (1)由于被积函数是奇函数,因此.(2)由于被积函数是奇函数,因此.(3).(4).(5),易看出被积函数是
1.用换元法计算下列各定积分.
(1)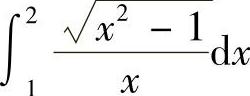 (2)
(2)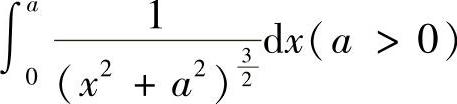
(3)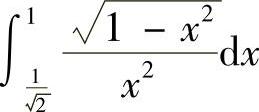 (4)
(4)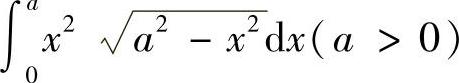
(5)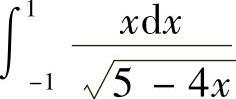 (6)
(6)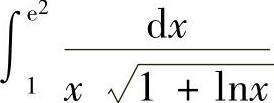
解 (1)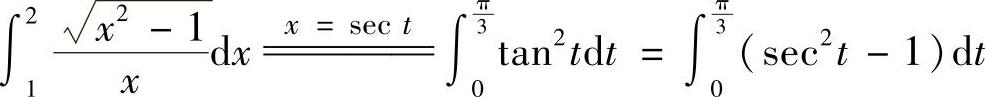
(2)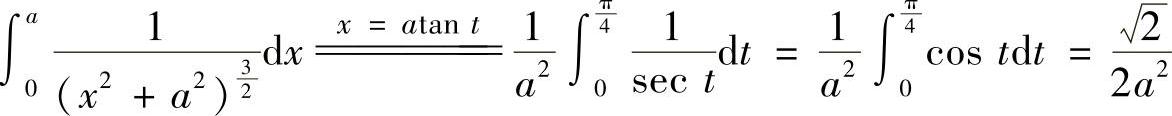
(3)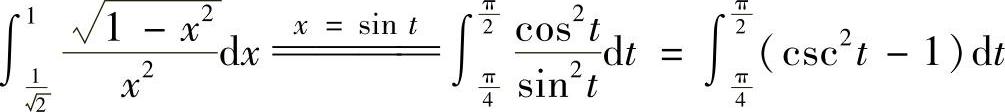
(4)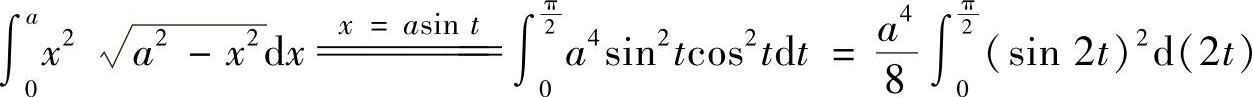
(5)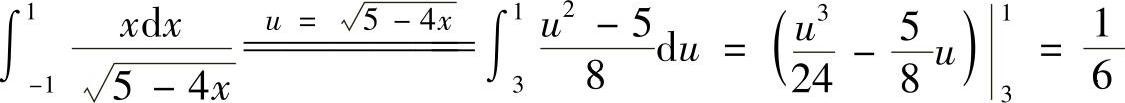
(6)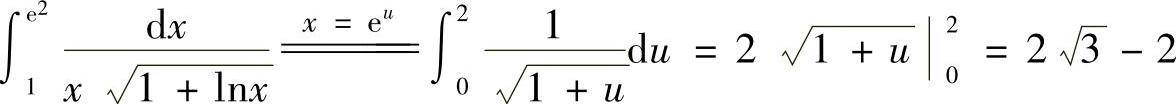
2.用分部积分计算下列各定积分.
(1)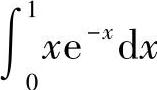 (2)
(2)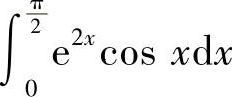
(3)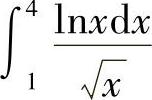
(4) (5)
(5)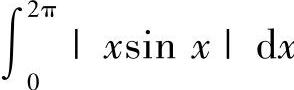 解(1)
解(1)
(2)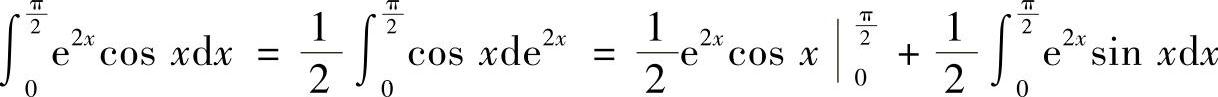
因此有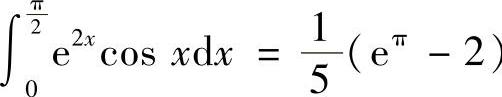 .
.
(3)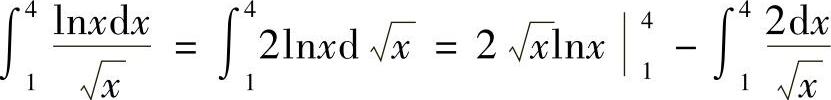
(4)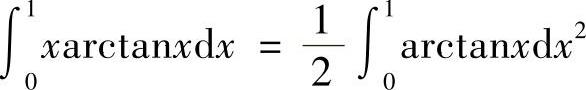
(5)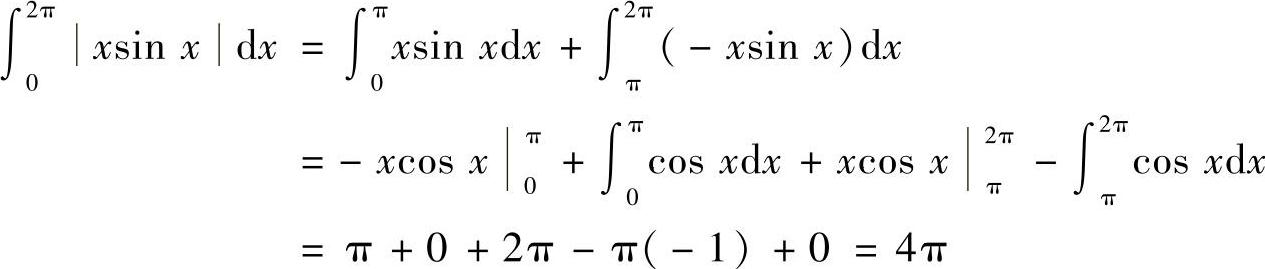
3.利用函数奇偶性计算下列各定积分.
(1)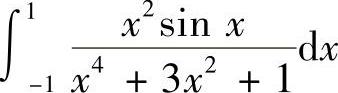 (2)
(2)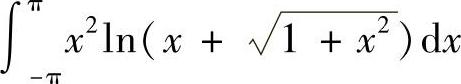
(3)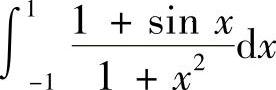 (4)
(4)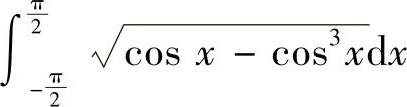
(5)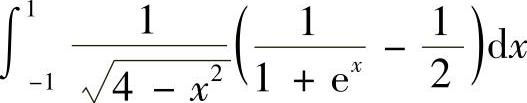
解 (1)由于被积函数是奇函数,因此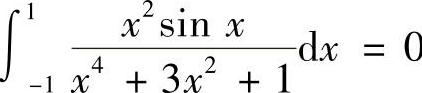 .
.
(2)由于被积函数是奇函数,因此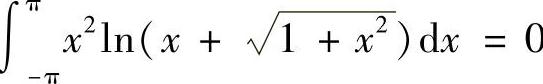 .
.
(3)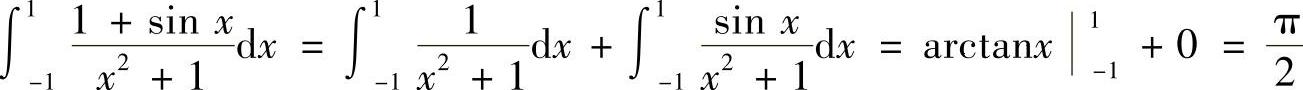 .
.
(4)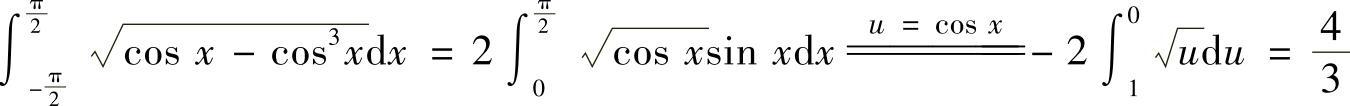 .
.
(5)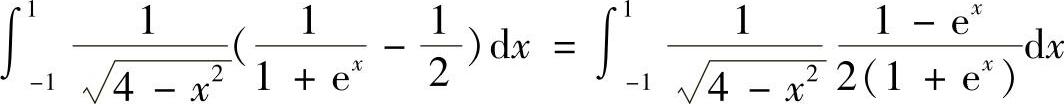 ,易看出被积函数是奇函数,则有
,易看出被积函数是奇函数,则有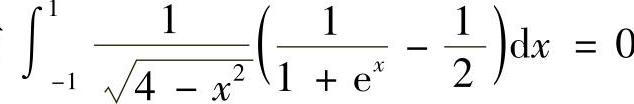 .
.
4.利用
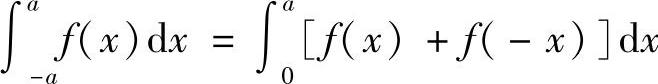 ,求∫
,求∫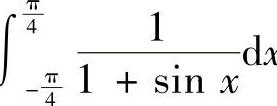 ×.
×.
解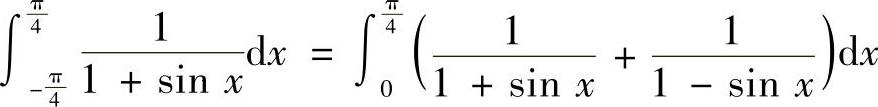
5.设函数公式
计算
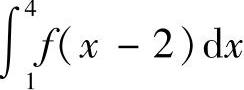 .(https://www.daowen.com)
.(https://www.daowen.com)
解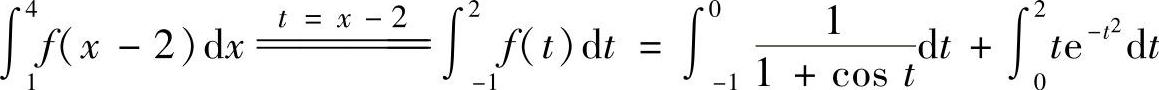
6.设f(×)连续,
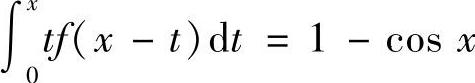 ,求
,求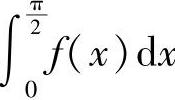 .
.
解
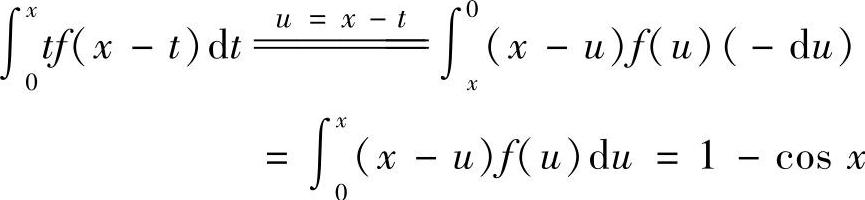 等式两边对×求导,则有
等式两边对×求导,则有
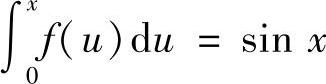 ,故有
,故有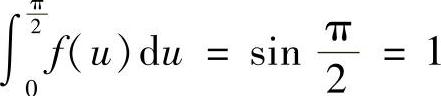 .
.
7.证明:(1)若f(×)为连续的偶函数,则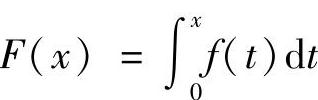 为奇函数;
为奇函数;
(2)若f(×)为连续的奇函数,则
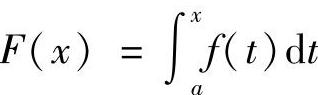 为偶函数(A为任意
为偶函数(A为任意
常数).
证(1)因为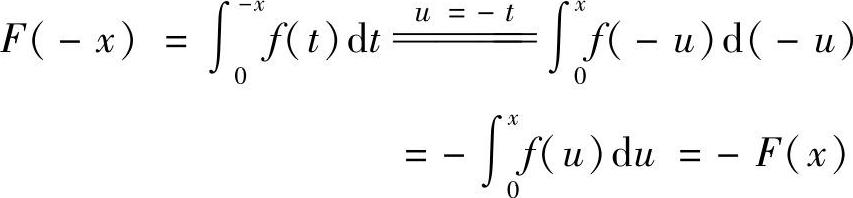
所以f(×)为奇函数.
(2)因为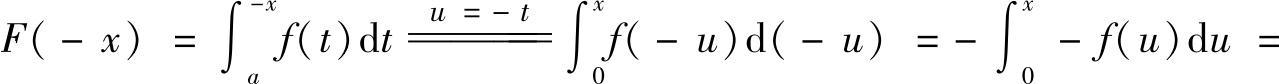 f(×),所以f(×)为偶函数.
f(×),所以f(×)为偶函数.
8.证明
.
证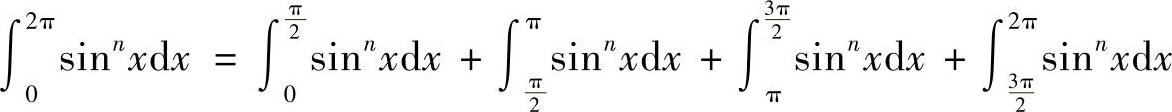 而
而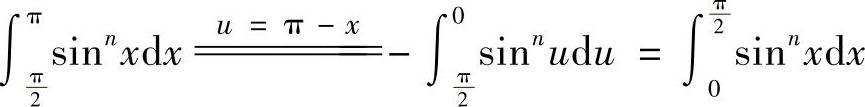
所以,当N为偶数时,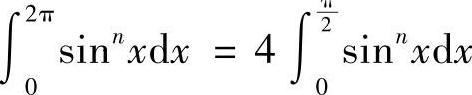 ,
,
当N为奇数时,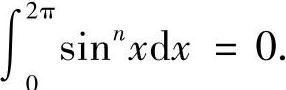
9.设f(π)=1,且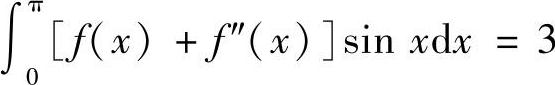 ,求f(0).
,求f(0).
解
而f(π)=1,所以f(0)=2.
10.设函数f(×)在(-∞,+∞)内满足f(×)=f(×-π)+SIN×,且f(×)=×,×∈[0,π],计算
解
11.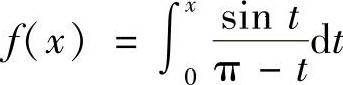 ,计算
,计算
解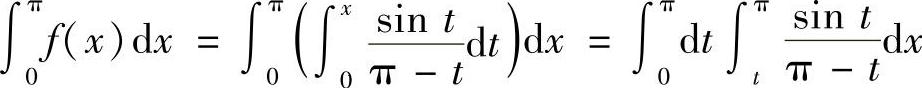
注 本题利用了二重积分中交换积分次序.
12.设f(×)为连续函数,且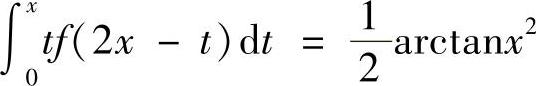 ,已知f(1)=1,求
,已知f(1)=1,求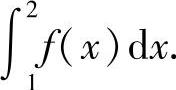
解 令2×-t=u,则
方程两边对×求导,可得
又因为f(1)=1,所以有
13.设f(×)为连续函数,且f(0)≠0,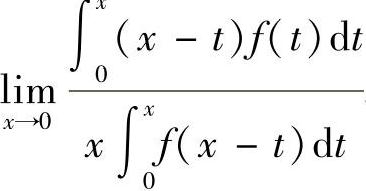
解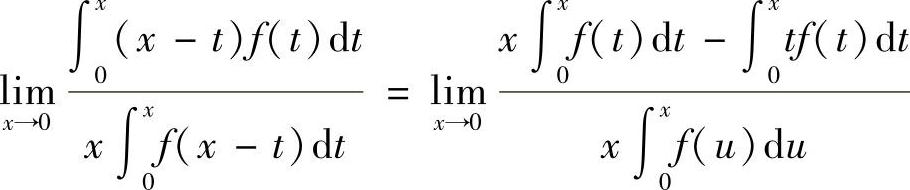
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







