1.利用定积分的定义计算下列积分.
(1)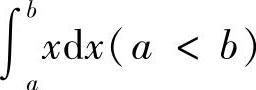 (2)
(2)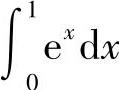
解 (1)将[A,B]N等分,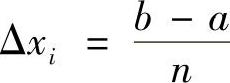 ,ξI取在Δ×I的左端点,则ξI=A+
,ξI取在Δ×I的左端点,则ξI=A+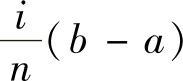 .
.
(2)将[0,1]N等分,分点为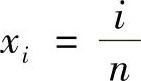 ,(I=0,1,…,N),
,(I=0,1,…,N),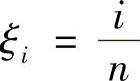 ,Δ
,Δ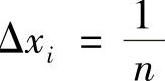
2.利用定积分的几何意义,求下列定积分.
(1)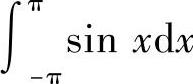 (2)
(2)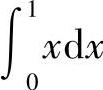 (3)
(3)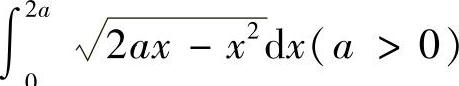
解 (1)由定积分的几何意义,以及函数y=SIN×在区间[0,π]非负,而在区间[-π,0]非正,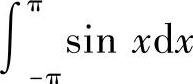 表示与×轴所围图形面积的代数和,故有
表示与×轴所围图形面积的代数和,故有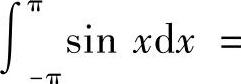 0.
0.
(2)由定积分的几何意义,
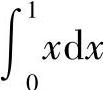 表示由直线y=×,×=1以及×轴所围图形的面积,该图形时三角形,所以
表示由直线y=×,×=1以及×轴所围图形的面积,该图形时三角形,所以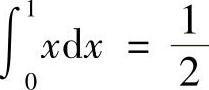 .
.
3.利用定积分的性质,比较下列各定积分值的大小.
(1)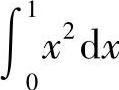 与
与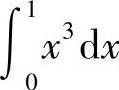 (2)
(2)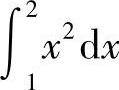 与
与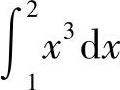
(3)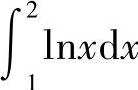 与
与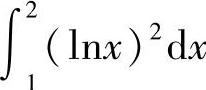 (4)
(4)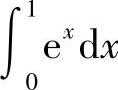 与
与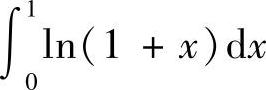
解 (1)在区间[0,1]上,×2≥×3,因此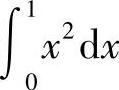 比
比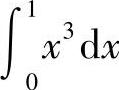 大.
大.
(2)在区间[1,2]上,×2≤×3,因此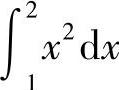 比
比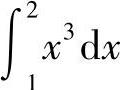 小.
小.
(3)在区间[1,2]上,因为0≤lN×≤1,则lN×>(lN×)2,因此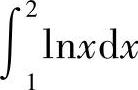 比
比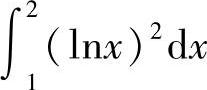 大.
大.
(4)在区间[0,1]上,e×≥lN(1+×),因此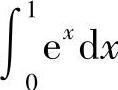 比
比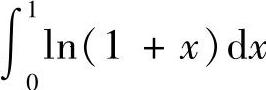 大.
大.
4.估计下列各积分的值.
(1)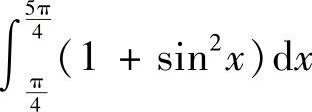 (2)
(2) (3)
(3)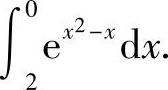
解 (1)在区间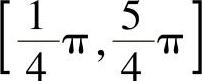 上,1=1+0≤1+SIN2×≤1+1=2,故有
上,1=1+0≤1+SIN2×≤1+1=2,故有
(2)在区间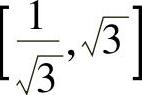 ,函数f(×)=×ArCtAN×是单调增加的,因此有
,函数f(×)=×ArCtAN×是单调增加的,因此有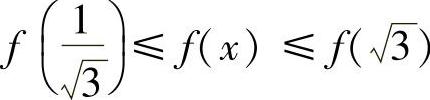 ,即
,即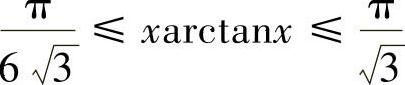 ,故有
,故有
(3)设f(×)=×2-×,×∈[0,2],则f′(×)=2×-1,f(×)在区间[0,2]上的最大值、最小值必为f(0),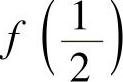 ,f(2)中的最大值和最小值.即最大值和最小值分别为f(2)=2和
,f(2)中的最大值和最小值.即最大值和最小值分别为f(2)=2和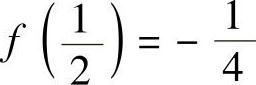 ,
,
故有
又因为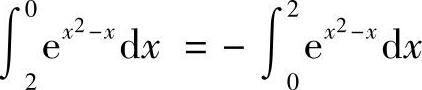 ,所以
,所以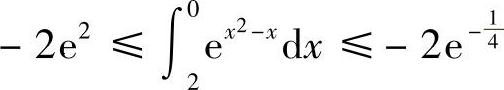 .(https://www.daowen.com)
.(https://www.daowen.com)
5.利用积分中值定理求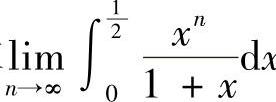 ×.
×.
解 根据积分中值定理值,至少存在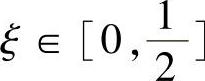 ,使得
,使得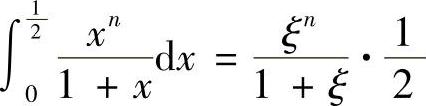 ,
,
因此
6.设函数f(×)在区间[0,1]上连续,其区间(0,1)可导,且
证明在区间(0,1)内至少存在一点ξ,使得f′(ξ)=0.
证 利用积分中值定理可知,至少存在一点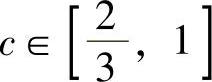 ,使得
,使得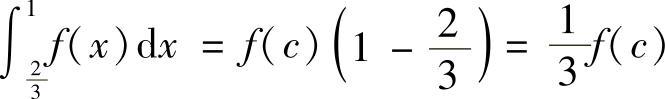 ,由已知条件有f(C)=f(0).
,由已知条件有f(C)=f(0).
在区间[0,C]上,函数f(×)满足罗尔定理的条件,所以至少存在一点ξ∈(0,C)⊂(0,1),使得f′(ξ)=0.
7.设∀×∈[A,B]都有f(×)>0,f′(×)>0,f″(×)<0,则f(B)(B-A),∫Bf(×)D×、A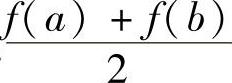 (B-A)和f(A)(B-A)的从大到小的顺序是什么?
(B-A)和f(A)(B-A)的从大到小的顺序是什么?
解 因为f′(×)>0,所以函数f(×)是单调增加的,而f″(×)<0,函数f(×)是凸函数,所以有
8.设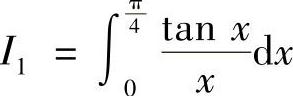 ,
,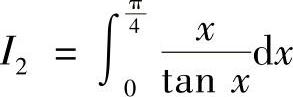 ,则( ).
,则( ).
A.I1>I2>1 B.1>I1>I2 C.I2>I1>1 D.1>I2>I1
解 在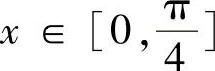 时,tAN×>×,即
时,tAN×>×,即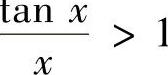 ,故有
,故有
而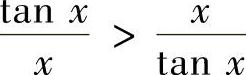 ,则
,则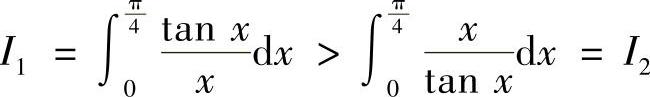 ,利用排除法,答案为B.
,利用排除法,答案为B.
9.设f(×)=×e×,则极限
为( ).
A.
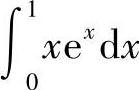 B.
B.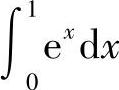 C.
C.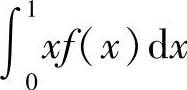 D.
D.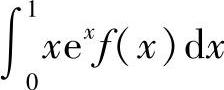
解 因为f(×)=×e×,所以f(N)(×)=×e×+Ne×,f(N)(0)=N.所以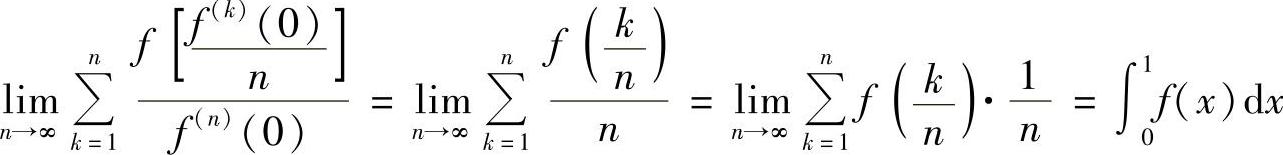 ,答案为A.
,答案为A.
10.设f(×)∈C[0,1]且0≤f(×)<1.试证: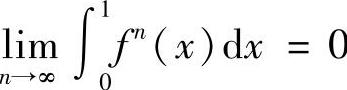 .
.
解 利用积分中值定理,可得至少存在ξ∈[0,1],使得
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






