微积分例题：验证和求解微分方程

1．验证ｙ₁＝CoSω×，ｙ₂＝SINω×都是微分方程ｙ″+ωｙ＝0的解，并写出该方程的通解．

证 易得ｙ′₁＝-ωSINω×，ｙ″₁＝-ω²CoSω×，将ｙ₁＝CoSω×，ｙ″₁＝-ω²CoSω×带入微分方程，显然方程变为了恒等式，故ｙ₁＝CoSω×是微分方程ｙ″+ωｙ＝0的解．

ｙ₂′＝ωCoSω×，ｙ″₂＝-ω²SINω×，将ｙ₂＝SINω×，ｙ″₂＝-ω²SINω×带入微分方程，显然方程变为了恒等式，故ｙ₂＝SINω×是微分方程ｙ″+ωｙ＝0的解．

解 微分方程的解ｙ₁＝CoSω×，ｙ₂＝SINω×是线性无关的，故由二阶线性其次方程解的性质知该方程的通解为

ｙ＝C₁CoSω×+C₂SINω×

2．验证ｙ₁＝e^×2，ｙ₂＝×e^×2都是微分方程ｙ″-4×ｙ′+（4ײ-2）ｙ＝0的解，并写出该方程的通解．

证 易得ｙ′₁＝2×e^×2，ｙ″₁＝2e^×2+4ײe^×2，将上两式与ｙ₁＝e^×2带入微分方程，显然方程变为了恒等式，故ｙ₁＝e^×2是微分方程ｙ″-4×ｙ′+（4ײ-2）ｙ＝0的解．

易得ｙ₂′＝e^×2+2ײe^×2，ｙ″₂＝6×e^×2+4׳e^×2，将上两式与ｙ₂＝×e^×2带入微分方程，显然方程变为了恒等式，故ｙ₂＝×e^×2是微分方程ｙ″-4×ｙ′+（4ײ-2）ｙ＝0的解．

解 微分方程的解ｙ₁＝e^×2，ｙ₂＝×e^×2是线性无关的，故由二阶线性其次方程解的性质知该方程的通解为

ｙ＝C₁e^×2+C₂×e^×2

即

ｙ＝e^×2（C₁+C₂×）

3．已知ｙ₁＝3，ｙ₂＝3+ײ，ｙ₃＝3+ײ+e^×都是微分方程

（ײ-2×）ｙ″-（ײ-2）ｙ′+（2×-2）ｙ＝6×-6的解，求该方程的通解．

解 微分方程有特解ｙ₁＝3，显然ｙ＝ײ和ｙ＝ײ+e^×是微分方程所对应的齐次方程的两个线性无关的解，故由线性非齐次方程的解的结构知原方程的通解为

ｙ＝C₁ײ+C₂e^×+3

4．已知ｙ₁＝CoS×，ｙ₂＝SIN×都是微分方程ｙ″+ｙ＝0的解，ｙ∗＝ײ-2是ｙ″+ｙ＝ײ的解，求ｙ″+ｙ＝ײ的通解．

解 由条件知ｙ₁＝CoS×，ｙ₂＝SIN×是方程ｙ″+ｙ＝ײ所对应的齐次方程的两个线性无关的解，故由线性非齐次方程的解的结构知原方程的通解为

ｙ＝C₁CoS×+C₂CoS×+ײ-2

5．求下列微分方程的通解或在给定条件下的特解．

（1）ｙ″-2ｙ′-3ｙ＝0

（2）ｙ″+4ｙ′+4ｙ＝0

（3）ｙ″+2ｙ′+5ｙ＝0

（4）ｙ″+3ｙ′+2ｙ＝0，ｙ′丨_×＝0＝1，ｙ丨_×＝0＝1

（5）ｙ″+25ｙ＝0，ｙ′丨_×＝0＝5，ｙ丨_×＝0＝2

（6）4ｙ″+4ｙ′+ｙ＝0，ｙ′丨_×＝0＝0，ｙ丨_×＝0＝2

解 （1）特征方程为

λ²-2λ-3＝0

特征根为

λ₁＝-1，λ₂＝3

故方程的通解为

ｙ＝C₁e^-×+C₂e^3×

（2）特征方程为

λ²+4λ+4＝0

特征根为

λ₁＝λ₂＝-2

故方程的通解为

ｙ＝C₁e^-2×+C₂×e^-2×＝e^-2×（C₁+C₂×）

（3）特征方程为

λ²+2λ+5＝0

特征根为

λ＝-1±2I

故方程的通解为

ｙ＝e^-×（C₁CoS2×+C₂SIN2×）

（4）特征方程为

λ²+3λ+2＝0

特征根为

λ₁＝-2，λ₂＝-1

故方程的通解为

ｙ＝C₁e^-2×+C₂e^-×

将ｙ_×＝0＝1代入通解，得C₁+C₂＝1．由ｙ′＝-2C₁e^-2×-C₂e^-×，以ｙ′_×＝0＝1

代入得-2C₁-C₂＝1．因此C₁＝-2，C₂＝3，故所求特解为

ｙ＝-2e^-2×+3e^-×

（5）特征方程为

λ²+25＝0

特征根为

λ＝±5I

故方程的通解为

ｙ＝C₁CoS5×+C₂SIN5×

将ｙ丨_×＝0＝2代入通解，得C₁＝2，从而ｙ＝2CoS5×+C₂SIN5×

由ｙ′＝-10SIN5×+5C₂CoS5×，以ｙ′丨_×＝0＝5代入得C₂＝1．故所求特解为

ｙ＝2CoS5×+SIN5×

（6）特征方程为

4λ²+4λ+1＝0

特征根为

故方程的通解为

将ｙ_×＝0＝2代入通解，得C₁＝2，从而．

由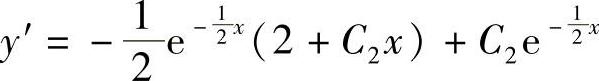，以ｙ′_×＝0＝0代入得C₂＝1． 故所求特解为

6.求下列微分方程的通解或在给定条件下的特解．

（1）ｙ″-5ｙ′+6ｙ＝×e^×

（2）ｙ″-2ｙ′-3ｙ＝3×+1

（3）ｙ″+ｙ＝2×+1

（4）ｙ″-2ｙ′+5ｙ＝CoS2×

（5）ｙ″+ｙ′-2ｙ＝e^-2×SIN×

（6）ｙ″-2ｙ′-e^2×＝0，ｙ′_×＝0＝1，ｙ_×＝0＝1

解 （1）齐次方程的特征方程为λ²-5λ+6＝0，其特征根为λ₁＝2，λ₂＝3．因此对应的齐次方程的通解为

C₁e^2×+C2e^3×

再求非齐次方程的特解．因α＝1不是特征方程的根，故设特解为

ｙ^∗＝（A×+B）e^×

则ｙ^∗′＝（A×+A+B）e^×，ｙ^∗″＝（A×+2A+B）e^×．将ｙ∗，ｙ∗′，ｙ∗″代入原方程得

2A×-3A+2B＝×

比较系数得，解得．

因此，非齐次方程的特解为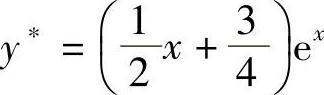

所以，原方程的通解为

（2）齐次方程的特征方程为λ²-2λ-3＝0，其特征根为λ₁＝-1，λ₂＝3．因此对应的齐次方程的通解为

C₁e^-×+C₂e_3×

再求非齐次方程的特解．因α＝0不是特征方程的根，故设特解为

ｙ^∗＝A×+B

则ｙ^∗′＝A，ｙ∗″＝0．将ｙ∗，ｙ^∗′，ｙ^∗″代入原方程得

-2A-3A×-3B＝3×+1

比较系数得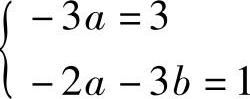，解得．

因此，非齐次方程的特解为

所以，原方程的通解为

（3）齐次方程的特征方程为λ²+1＝0，其特征根为λ＝±I．因此对应的齐次方程的通解为

C₁CoS×+C₂SIN×

再求非齐次方程的特解．因α＝0不是特征方程的根，故设特解为

ｙ^∗＝A×+B(https://www.daowen.com)

则ｙ^∗′＝A，ｙ^∗″＝0．将ｙ^∗，ｙ^∗′，ｙ^∗″代入原方程得

A×+B＝2×+1

比较系数得．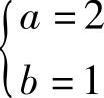

因此，非齐次方程的特解为

ｙ^∗＝2×+1

所以，原方程的通解为

ｙ＝C₁CoS×+C₂SIN×+2×+1

（4）齐次方程的特征方程为λ²-2λ+5＝0，其特征根为λ＝1±2I．因此对应的齐次方程的通解为

e^×（C₁CoS2×+C₂SIN2×）

再求非齐次方程的特解．因α+Iβ＝0+2I不是特征方程的根，故设特解为

ｙ^∗＝ACoS2×+BSIN2×

则ｙ^∗′＝-2ASIN2×+2BCoS2×，ｙ∗″＝-4ACoS2×-4BSIN2×．将ｙ^∗，ｙ^∗′，ｙ^∗″代入

原方程整理得

（A-4B）CoS2×+（4A+B）SIN2×＝CoS2×

比较系数得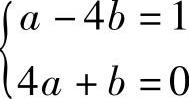，解得．

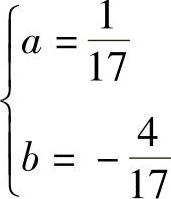因此，非齐次方程的特解为

所以，原方程的通解为

（5）齐次方程的特征方程为λ²+λ-2＝0，其特征根为λ₁＝-2，λ₂＝1．因此对应的齐次方程的通解为

C₁e^-2×+C₂e^×

再求非齐次方程的特解．因α+Iβ＝-2+I不是特征方程的根，故设特解为

ｙ∗＝（ACoS×+BSIN×）e^-2×

则

ｙ∗′＝［（-A-2B）SIN×+（B-2A）CoS×］e^-2×

ｙ∗″＝［（4A+3B）SIN×+（3A-4B）CoS×］e^-2×

将ｙ∗，ｙ∗′，ｙ∗″代入原方程整理得

（3A-B）SIN×-（A+3B）CoS×＝SIN×

比较系数得

，解得

．

因此，非齐次方程的特解为

所以，原方程的通解为

（6）齐次方程的特征方程为λ²-2λ＝0，其特征根为λ₁＝0，λ₂＝2．因此对应的齐次方程的通解为

C₁+C₂e^2×

再求非齐次方程的特解．因α＝2是特征方程的一重根，故设特解为

ｙ^∗＝A×e^2×

则ｙ^∗′＝A（1+2×）e^2×，ｙ^∗″＝4A（1+×）e^2×．将ｙ^∗，ｙ^∗′，ｙ^∗″代入原方程整理得．

因此，非齐次方程的特解为

所以，原方程的通解为

将ｙ_×＝0＝1代入通解，得C₁+C₂＝1．由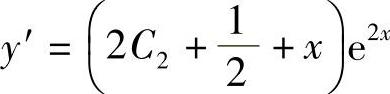，以ｙ′_×＝0＝1代入得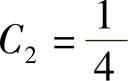，因此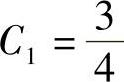．故所求特解为

7．设函数ｙ＝ｙ（×）满足ｙ″-3ｙ′+2ｙ＝2e^×，且其图像在点（0，1）处的切线与曲线ｙ＝ײ-×+1在该点的切线重合，求函数ｙ＝ｙ（×）．

解　曲线ｙ＝ײ-×+1在点（0，1）处的切线斜率为ｙ′_×＝0＝2×-1_×＝0＝-1，故由题意知函数ｙ＝ｙ（×）在点（0，1）处的切线斜率也是-1，即ｙ＝ｙ（×）满足初始条件ｙ′_×＝0＝-1，且显然函数过点（0，1），即ｙ_×＝0＝1．

微分方程ｙ″-3ｙ′+2ｙ＝2e^×所对应的齐次方程的特征方程为λ²-3λ+2＝0，其特征根为λ₁＝1，λ₂＝2．因此对应的齐次方程的通解为

C₁e^×+C₂e^2×

再求非齐次方程的特解．因α＝1是特征方程的一重根，故设特解为

ｙ^∗＝A×e^×

则ｙ^∗′＝A（1+×）e^×，ｙ^∗″＝A（2+×）e^×．将ｙ^∗，ｙ^∗′，ｙ^∗″代入原微分方程整理得A＝-2．

因此，非齐次方程的特解为

ｙ^∗＝-2×e^×

所以，原方程的通解为

ｙ＝C₁e^×+C₂e^2×-2×e^×＝（C₁-2×）e^×+C₂e^2×

将初始条件ｙ_×＝0＝1代入上式，得C₁+C₂＝1．由ｙ′＝（C₁-2×-2）e^×+2C₂e^2×，以ｙ′_×＝0＝-1代入得C₁+2C₂＝1，因此C₁＝1，C₂＝0．故所求函数ｙ＝ｙ（×）为

ｙ＝（1-2×）e×

8．设函数φ（×）连续，且满足

，求φ（×）．

解 显然φ（0）＝1．两边求导得

，即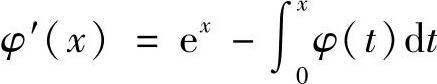易知φ′（0）＝1．上式再次求导得

φ″（×）+φ（×）＝e^×

其所对应的齐次方程的特征方程λ²+1＝0的特征根为λ＝±I，于是对应齐次方程的通解为

C₁CoS×+C₂SIN×

再求非齐次方程的特解．因α＝1不是特征方程的根，故设特解为

ｙ^∗＝Ae×

则ｙ^∗′＝ｙ^∗″＝Ae^×．将ｙ^∗，ｙ^∗′，ｙ^∗″代入原微分方程整理得．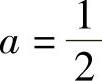

因此，非齐次方程的特解为

所以，原方程的通解为

将φ（0）＝1代入上式得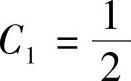．由，以φ′（0）＝1代入可得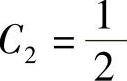，因此所求函数

9．已知二阶常系数非齐次线性微分方程有两个特解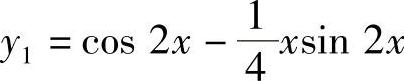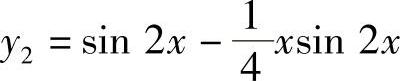，，求此微分方程．

解 设所求微分方程为ｙ″+Aｙ′+Bｙ＝f（×）．由于ｙ₁，ｙ₂都是微分方程的解，故将ｙ₁，ｙ₂代入微分方程，则微分方程都应变为恒等式．根据ｙ₁，ｙ₂的特点知，两个恒等式相减，可得

（CoS2×）″-（SIN2×）″+A（CoS2×）′-A（SIN2×）′+BCoS2×-BSIN2×＝0

即

（-4-2A+B）CoS2×+（4-2A-B）SIN2×＝0

比较系数得方程组

解得

A＝0，B＝4

故微分方程为

ｙ″+4ｙ＝f（×）

将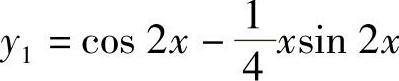，，ｙ″₁＝-5CoS2×+×SIN2×代入上式，则可得f（×）＝-CoS2×．因此所求微分方程为

ｙ″+4ｙ＝-CoS2×

10．设ｙ＝e^2×+（1+×）e^×是二阶常系数非齐次线性微分方程ｙ″+αｙ′+βｙ＝γe^×的一个特解，求α²+β²+γ²．

解 易知ｙ′＝2e^2×+（2+×）e^×，ｙ″＝4e^2×+（3+×）e^×．因为ｙ＝e^2×+（1+×）e^×是方程的解，故将ｙ，ｙ′，ｙ″代入微分方程，微分方程应变为恒等式，即

（4+2α+β）e^2×+（3+2α+β）e^×+（1+α+β）×e^×＝γe×

比较系数得方程组

解得

α＝-3，β＝2，γ＝1

故

α²+β²+γ²＝14

11．设ｙ＝ｙ（×）在（-∞，+∞）内具有二阶导数，且ｙ′≠0，×＝×（ｙ）是ｙ＝ｙ（×）的反函数，试求微分方程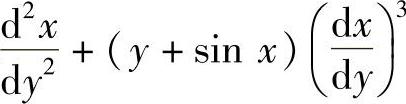＝0的通解．

解 由×＝×（ｙ）是ｙ＝ｙ（×）的反函数，故由反函数的求导法则知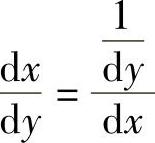，因此

故微分方程变为

微分方程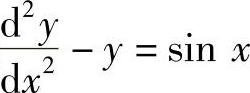

所对应的齐次方程的特征方程为λ²-1＝0，其特征根为λ₁＝1，λ₂＝-1．因此对应的齐次方程的通解为

C₁e^×+C₂e^-×

再求非齐次方程的特解．因α＝0是不是特征方程的根，故设特解为

ｙ^∗＝ACoS×+BSIN×

则ｙ^∗′＝-ASIN×+BCoS×，ｙ^∗″＝-ACoS×-BSIN×．将ｙ^∗，ｙ^∗′，ｙ^∗″代入非齐次微分方程整理得A＝0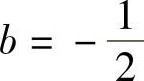，．因此，非齐次方程的特解为

所以，原方程的通解为