微分方程习题5.2：求解×ｙ′-ｙlNｙ＝0

1．求下列微分方程的通解或在给定条件下的特解．

（1）×ｙ′-ｙlNｙ＝0

（2）

（3）SeC²×ｔANｙD×+SeC²ｙｔAN×Dｙ＝0

（4）CoS×SINｙD×+SIN×CoSｙDｙ＝0

（5）（e^×+ｙ-e^×）D×+（e^×+ｙ+e^ｙ）Dｙ＝0

（6）

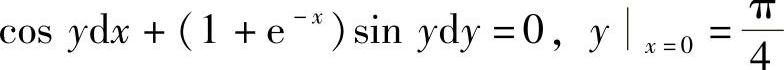
（7）

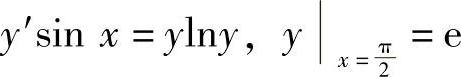
（8）

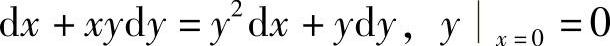
解 （1）方程可变形为

两边积分得

丨丨N丨丨Nｙ丨＝丨lN丨×丨+C₁

故所求通解为

lNｙ＝C×

即

ｙ＝e^C×（C为任意常数）

（2）方程可变形为

两边积分得

故所求通解为

（3）方程可变形为

即

两边积分得

lN丨ｔANｙ丨＝-lN丨ｔAN×丨+C₁

故所求通解为

ｔAN×ｔANｙ＝C（C为任意常数）

（4）方程可变形为

即

两边积分得

lN丨SINｙ丨＝-lN丨SIN×丨+C₁

故所求通解为

SIN×SINｙ＝C（C为任意常数）

（5）方程可变形为

即

两边积分得

lN丨e^ｙ-1丨＝-lN丨e^×+1丨+C₁

故所求通解为

（e^×+1）（e^ｙ-1）＝C（C为任意常数）

（6）方程可变形为

即

两边积分得

lN丨CoSｙ丨＝lN丨e^×+1丨+C₁

故所求通解为

（e^×+1）SeCｙ＝C（C为任意常数）

代入初始条件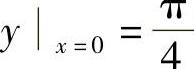得，，故所求特解为

（7）方程可变形为

即

两边积分得

故所求通解为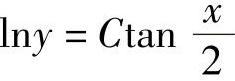(C为任意常数)代入初始条件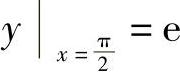得，C＝1，故所求特解为

（8）方程可变形为

即

两边积分得

lN丨1-ｙ²丨＝2lN丨1-×丨+C₁

故所求通解为

1-ｙ²＝C（1-×）²（C为任意常数）

代入初始条件ｙ丨_×＝0＝0得，C＝1，故所求特解为

1-ｙ²＝（1-×）²

2．求下列微分方程的通解或在给定条件下的特解．

（1）

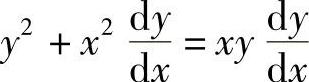
（2）

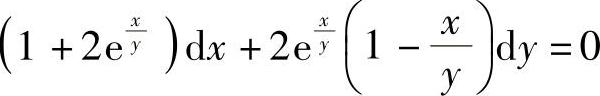
（3）

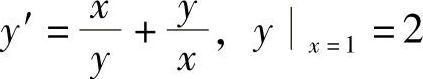
（4）（ײ+2×ｙ-ｙ²）D×+（ｙ²+2×ｙ-ײ）Dｙ＝0，ｙ_×＝1＝1

（5）

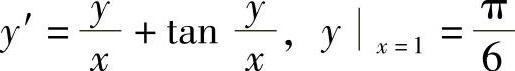
（6）（ｙ²-3ײ）Dｙ+2×ｙD×＝0

解 （1）方程两边同除以ײ得

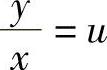令，则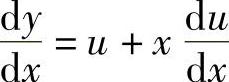，代入上式，得

即

变量分离得

两边积分得

ｕ-lN丨ｕ丨＝lN丨×丨+C

故所求通解为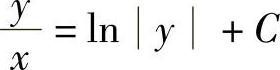（C为任意常数）

（2）方程两边同除以Dｙ得

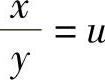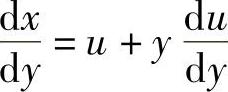令，则，代入上式，得

即

变量分离得

两边积分得

lN丨ｕ+2e^ｕ丨＝-lN丨ｙ丨+C₁

故所求通解为

ｙ（ｕ+2e^ｕ）＝C（C为任意常数）

即

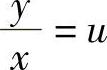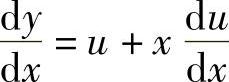（3）令，则，代入方程，得

变量分离得

两边积分得

故原方程的通解为

ｙ²＝2ײ（C+lN丨×丨）（C为任意常数）

代入初始条件ｙ_×＝1＝2得，C＝2，故所求特解为

ｙ²＝2ײ（2+lN丨×丨）

（4）方程两边同除以ײD×得

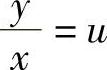令，则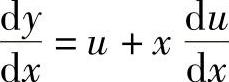，代入上式，得

变量分离得

即

两边积分得

故通解为

因此原方程的通解为

代入初始条件ｙ_×＝1＝1得，C＝1，故所求特解为

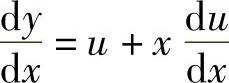（5）令，则，代入方程，得

变量分离得

即

两边积分得

lN丨SINｕ＝lN丨×丨+C₁

故通解为

SINｕ＝C×（C为任意常数）

因此原方程的通解为

代入初始条件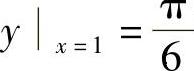得，，故所求特解为

（6）方程两边同除以ｙ²Dｙ得(https://www.daowen.com)

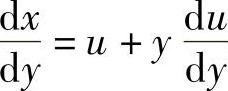令，则，代入上式，得

即

变量分离得

即

两边积分得

lN丨ｕ²-1丨＝lN丨ｙ丨+C

故通解为

ｕ²-1＝Cｙ（C为任意常数）

因此原方程的通解为

ײ-ｙ²＝Cｙ³（C为任意常数）

3．设商品A和商品B的售价分别为P₁，P₂，已知价格P₁与价格P₂相关，且价格P₁相对P₂的弹性为

，求P₁与P₂的函数关系式．

解 方程可变形为

令，则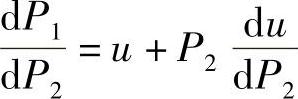，代入上式，得

即

变量分离得

两边积分得

故通解为

因此原方程的通解为

4．某商品的需求量×对价格P的弹性为η＝-3P³，市场对该产品的最大需求量为1（万件），求需求函数．

解 由条件知有微分方程

变量分离得

两边积分得

ｌN×＝-P³+C₁

故通解为

×＝Ce^-P3（C为任意常数）

由于需求量最大为1，即当P＝0时有×＝1，故C＝1，因此需求函数为×＝e^-P3．

5． 求下列微分方程的通解或在给定条件下的特解．

（1）ｙ′+ｙCoS×＝e^-SIN×

（2）ｙｌNｙD×+（×-ｌNｙ）Dｙ＝0

（3）×ｙ′-2ｙ＝׳e^×，ｙ_×＝1＝0

（4）ｙ+ｙCoｔ×＝5e^CoS×，ｙ_×＝1＝0

（5）（ｙ²-6×）Dｙ+2ｙD×＝0，ｙ_×＝1＝1

解 （1）令P（×）＝CoS×，Ｑ（×）＝e^-SIN×，则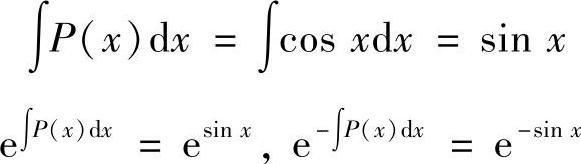

方程的通解为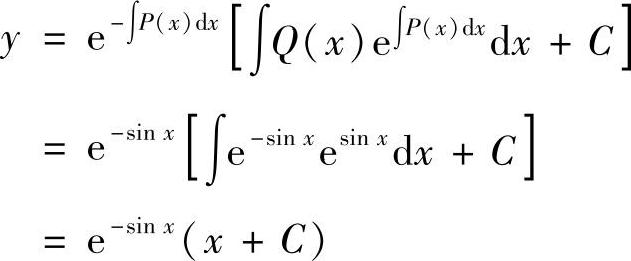

（2）方程两边同除以ｙlNｙDｙ，整理得

令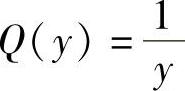，，则

方程的通解为

即

（3）方程可变形为

令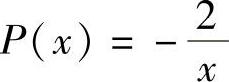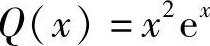，，则

方程的通解为

代入初始条件ｙ_×＝1＝0得，C＝-e，故所求特解为

ｙ＝ײ（e^×-e）

（4）令P（×）＝Coｔ×，Ｑ（×）＝5e^CoS×，则

方程的通解为

即通解为

ｙSIN×+5e^CoS×＝C

代入初始条件ｙ_×＝1＝0得，C＝5e^CoS1，故所求特解为

ｙSIN×+5e^CoS×＝5e^CoS1

（5）方程两边同除以2ｙDｙ，整理得

令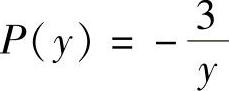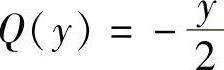，，则

方程的通解为

代入初始条件ｙ_×＝1＝1得，，故所求特解为．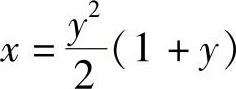

6．求连续函数f（×），使它满足

解 两边求导得

f′（×）+2f（×）＝2×

令P（×）＝2，Ｑ（×）＝2×，则

故有

又因为f（×）满足f（0）＝0，故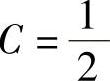，因此连续函数f．

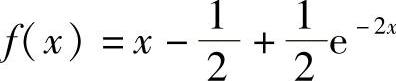7．求一曲线方程，该曲线通过原点，并且在点（×，ｙ）处的切线斜率等于2×+ｙ．

解 设曲线方程为ｙ＝f（×），则应满足方程f′（×）＝2×+ｙ．

令P（×）＝-1，Ｑ（×）＝2×，则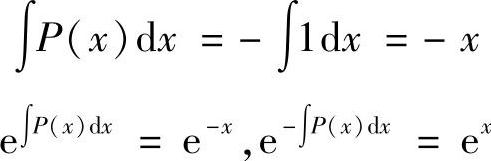

故有

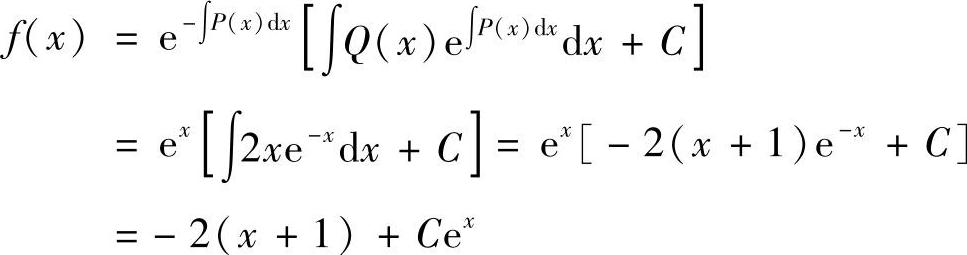又因为该曲线通过原点，故C＝2，因此曲线方程为ｙ＝2（e^×-×-1）．

8．已知生产某产品的固定成本为A＞0，生产×单位的边际成本与平均单位成本之差为，且当产量的数值等于A时，相应的总成本为2A，求总成本C与产量×的函数关系．

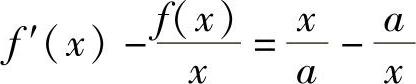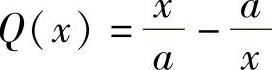解 设总成本C与产量×的函数关系为C＝f（×），则应满足方程令，，则

故有

又因为当产量的数值等A时，相应的总成本为2A，故C₁＝0，因此总成本C与产量×的函数关系为A．

9．求下列微分方程的通解．

（1）

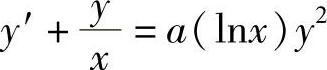
（2）ｙ′-3×ｙ＝×ｙ2

解 （1）这是一个伯努利方程，令ｚ＝ｙ^-1，则有．这是一阶线性方程，解得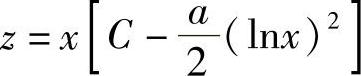

将ｚ换成ｙ^-1，即得原方程的通解为

（2）这是一个伯努利方程，令ｚ＝ｙ^-1，则有．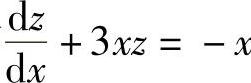

这是一阶线性方程，解得

即

将ｚ换成ｙ^-1，即得原方程的通解为

10．试求满足方程f′（×）+×f′（-×）＝×的f（×）．

解 由条件知

f′（-×）+（-×）f′（×）＝-×

上式乘以×与原方程做差，整理得

（1+ײ）f′（×）＝×+ײ

故

积分得

11．设函数ｙ（×）满足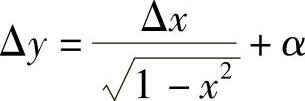，其中α为Δ×→0时的高阶无穷小，求ｙ（×）的表达式．

解 由条件知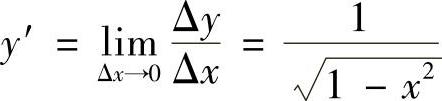，可变形为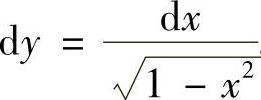．两边同时积分，得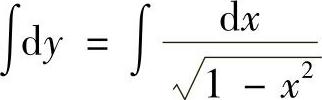，因此ｙ＝AｒCSIN ×+C．

12．设可导函数f（×）满足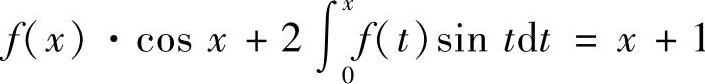，求f（×）．

解 方程两边同时求导得f′（×）·CoS×+f（×）SIN×＝1，可变形为一阶线性方程

f′（×）+f（×）ｔAN×＝SeC×

令P（×）＝ｔAN×，Ｑ（×）＝SeC×，则

13．设ｙ＝e^-×是微分方程×ｙ′+P（×）ｙ＝×的一个解，求此方程满足条件ｙ_×＝ｌN2＝1的特解．

解 由于ｙ＝e^-×是微分方程×ｙ′+P（×）ｙ＝×的一个解，故将ｙ＝e^-×和ｙ′＝-e^-×代入微分方程，则微分方程应变为恒等式，即-×e^-×+P（×）e^-×＝×，解得P（×）＝×e^×+×．从而微分方程变为一阶线性方程

ｙ′+（e^×+1）ｙ＝1

令P（×）＝e^×+1，Ｑ（×）＝1，则

代入初始条件ｙ丨_×＝lN2＝1得，C＝e²，故所求特解为

ｙ＝e^{-（e×+×-2）}+e^-×

14．设f（×）有连续的导函数，f′（0）＝e且对任意常数A，B，有f（A+B）＝e^Af（B）+e^2Bf（A），求f（×）．

解 将A＝B＝0代入上式，得f（0）＝0，故．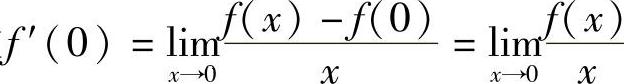

因此

从而有微分方程f′（×）-2f（×）＝e^×+1．令P（×）＝-2，Ｑ（×）＝e^×+1，则

将f（0）＝0代入上式，得C＝e，因此f（×）＝e（e^2×-e^×）．