1．试说出下列微分方程的阶数．

（1）×（ｙ′）2-2ｙｙ′+×＝0 （2）ײｙ″-×ｙ′+ｙ＝0

（3）（7×-6ｙ）D×+（×+ｙ）Dｙ＝0 （4）.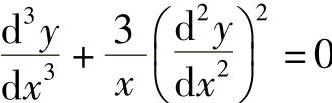

解 微分方程的阶是由微分方程中出现的未知函数的最高导数的阶数所确定的，故微分方程的阶数分别为（1）一阶，（2）二阶，（3）一阶，（4）三阶．

2．验证下列各给定函数是其对应微分方程的解．

（1）×ｙ′＝2ｙ，ｙ＝5ײ

（2）ｙ″+ｙ＝0，ｙ＝3SIN×-4CoS×

（3）ｙ″-（λ₁+λ₂）ｙ′+λ₁λ₂ｙ＝0，ｙ＝C₁e^λ1×+C₂eλ2×

（4）×ｙｙ″+×（ｙ′）2-ｙｙ′＝0，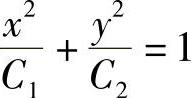

解 （1）由于ｙ＝5ײ，故ｙ′＝10×，代入微分方程，左端＝×·10×＝10ײ，右端＝2ｙ＝10ײ，故ｙ＝5ײ是微分方程的解．

（2）由于ｙ＝3SIN×-4CoS×，故ｙ′＝3CoS×+4SIN×，ｙ″＝-3SIN×+4CoS×，代入微分方程，

左端＝-3SIN×+4CoS×+3SIN×-4CoS×＝0

故ｙ＝3SIN×-4CoS×是微分方程的解．

（3）由于ｙ＝C₁e^λ1×+C₂e^λ2×，故ｙ′＝C₁λ₁e^λ1×+C₂λ₂e^λ2×，ｙ″＝C₁λ²₁e^λ1×+C₂λ²₂e^λ2×，代入微分方程，

左端＝C₁λ²₁e^λ1×+C₂λ²₂e^λ2×-（λ₁+λ₂）C₁λ₁e^λ1×+C₂λ₂e^λ2×+λ₁λ₂（C₁e^λ1×+C₂e^λ2×）＝0

故ｙ＝C₁e^λ1×+C₂e^λ2×是微分方程的解．

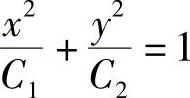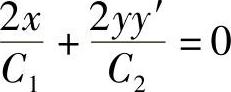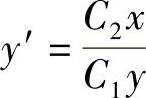（4）由两边同时对×求导得，，从而得到，此

式再对×求导得

代入微分方程，

故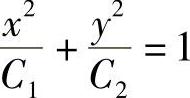是微分方程的解．(www.daowen.com)

3．在下列各题中，确定函数关系式中所含的参数，使函数满足所给的初始条件：

（1）ײ-ｙ²＝C，ｙ_×＝0＝5

（2）ｙ＝（C₁+C₂×）e^2×，ｙ_×＝0＝0，ｙ′_×＝0＝1

解 （1）将ｙ_×＝0＝5代入微分方程得0-25＝C，故C＝-25．

（2）将ｙ_×＝0＝0代入微分方程得0＝C₁，故C₁＝0，从而微分方程变为ｙ＝C₂×e^2×，因此ｙ′＝C₂e^2×+2C₂×e^2×，将ｙ′_×＝0＝1代入上式得，1＝C₂，故C₂＝1，C₁＝0．

4．设曲线在点（×，ｙ）处的切线的斜率等于该点横坐标的平方，试建立曲线所满足的微分方程．

解 曲线在点（×，ｙ）处的切线的斜率为ｙ′，故由条件知曲线所满足的微分方程为ｙ′＝ײ．

5．设函数ｙ＝（1+×）2ｕ（×）是方程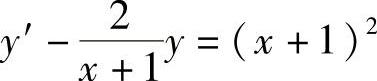的通解，求ｕ（×）．

解 由ｙ＝（1+×）2ｕ（×）可知ｙ′＝2（1+×）ｕ（×）+（1+×）2ｕ′（×），将上面两式代入方程得，

2（1+×）ｕ（×）+（1+×）2ｕ′（×）-2（1+×）ｕ（×）＝（1+×）2整理得ｕ′（×）＝1，故ｕ（×）＝×+C．

6．求连续函数f（×），使它满足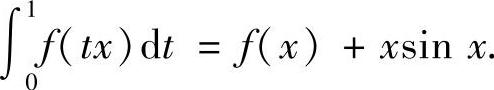

解 由于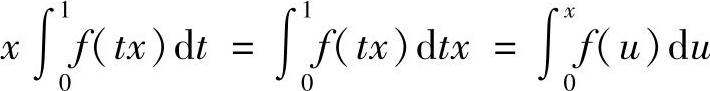，再由条件可得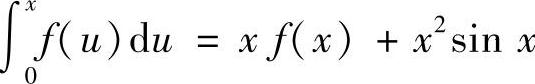上式两端对戈求导得，∫^×f（ｕ）Dｕ＝×f（×）+ײSIN×

上式两端对×求导

f（×）＝f（×）+×f′（×）+2×SIN×+ײCoS×

整理得

f′（×）＝-（2SIN×+×CoS×）

两边同时做0到×上的积分得，

f（×）＝CoS×-×SIN×+C