【摘要】:1.求下列不定积分.(1)∫Cot×D× (2)∫e3×+2D× (3)(4) (5) (6)(7) (8) (9)∫SIN3×CoS×D×(10)∫SIN2×CoS2×D× (11) (12)∫e×CoS(e×+1)D×(13) (14)解 (1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)2.求下列不定积分.(1) (2) (3)(4) (5) (6
1.求下列不定积分.(1)∫Cot×D× (2)∫e3×+2D× (3)
(4)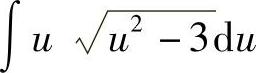 (5)
(5) (6)
(6)
(7)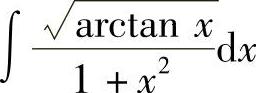 (8)
(8)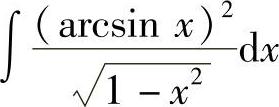 (9)∫SIN3×CoS×D×
(9)∫SIN3×CoS×D×
(10)∫SIN2×CoS2×D× (11) (12)∫e×CoS(e×+1)D×
(12)∫e×CoS(e×+1)D×
(13) (14)
(14)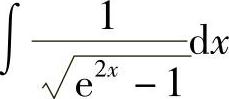
解 (1)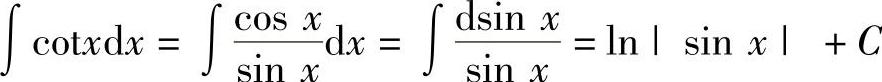
(2)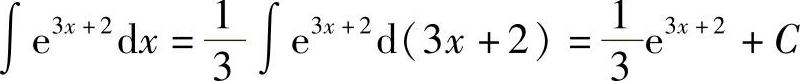
(3)
(4)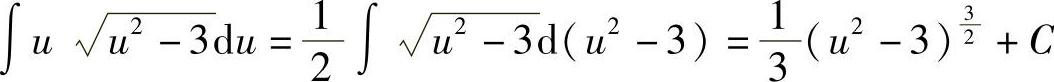
(5)
(6)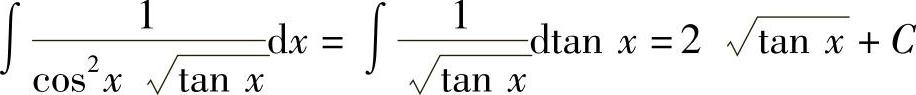
(7)
(8)
(9)
(10)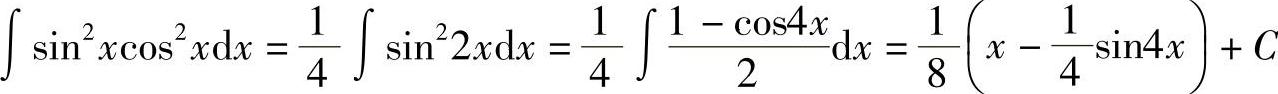
(11)
(12)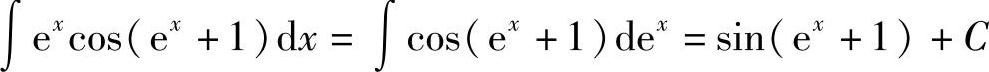
(13)
(14)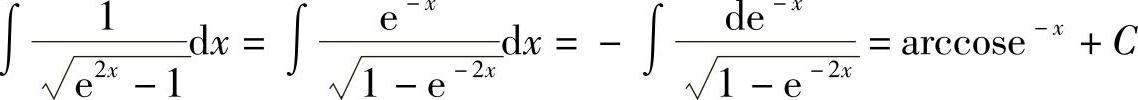
2.求下列不定积分.
(1) (2)
(2) (3)
(3)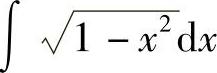
(4) (5)
(5)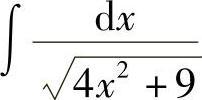 (6)
(6)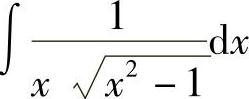 (7)
(7)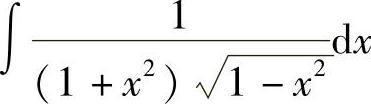 (8)
(8)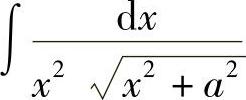 (9)
(9)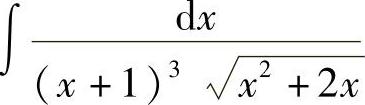
(10)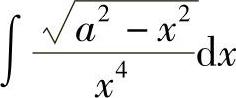
解 (1)令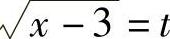 ,则×=t2+3,D×=2tDt,所以
,则×=t2+3,D×=2tDt,所以
(2)令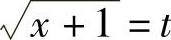 ,则×=t2-1,D×=2tDt,所以
,则×=t2-1,D×=2tDt,所以
(3)令×=SINt,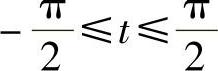 ,则D×=CoStDt,所以
,则D×=CoStDt,所以
由×=SIN t作辅助三角形得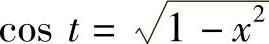 ,故
,故
(4)令×=SIN t,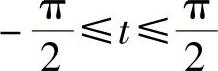 ,则D×=CoStDt,所以
,则D×=CoStDt,所以
由×=SIN t作辅助三角形得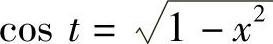 ,故
,故
(5)令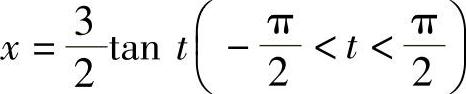 ,则
,则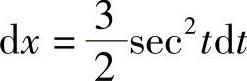 ,从而
,从而
故(https://www.daowen.com)
由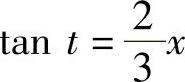 作辅助三角形,得
作辅助三角形,得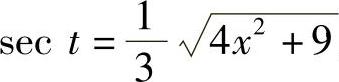 ,故
,故
(6)
(7)令×=SIN t,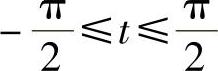 ,则D×=CoS tDt,所以
,则D×=CoS tDt,所以
(8)设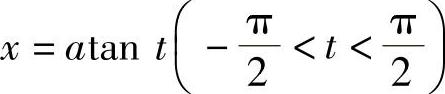 ,则D×=ASeC2tDt,
,则D×=ASeC2tDt,
从而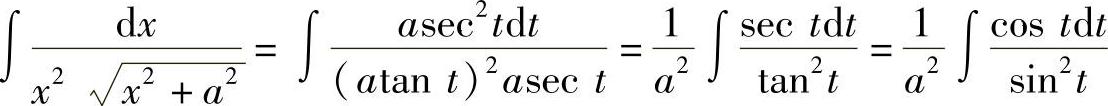
(9)令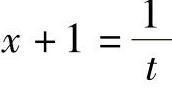 ,则
,则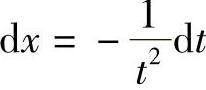 ,所以
,所以
由本题第三小题可知 ,故
,故
(10)令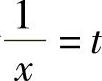 ,则
,则 ,所以
,所以
3.已知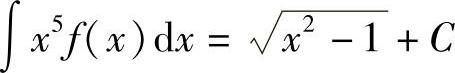 ,求∫f(×)D×.
,求∫f(×)D×.
解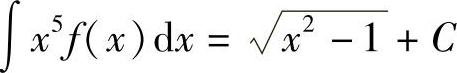 两边同时求导,得
两边同时求导,得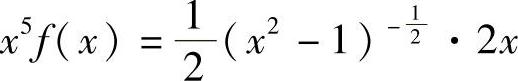 ,故
,故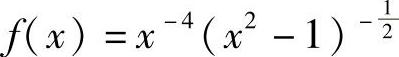 ,从而
,从而 ,令
,令 ,则D×=-t-2Dt,因此
,则D×=-t-2Dt,因此
4.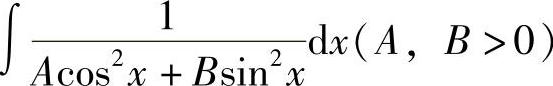 .
.
解
5.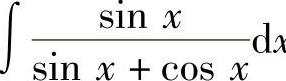 .
.
解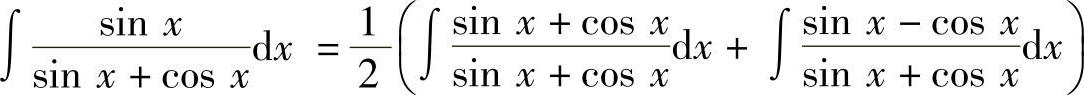
6. .
.
解
7.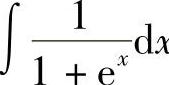 .
.
解: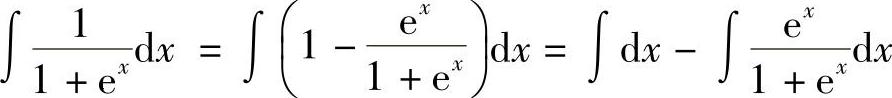
8.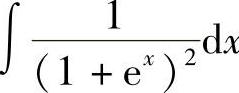 .
.
解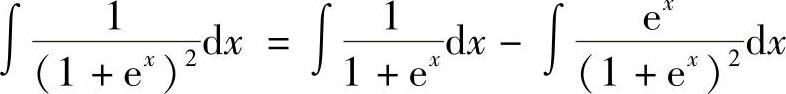
9.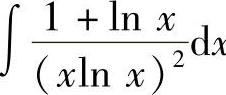 .
.
解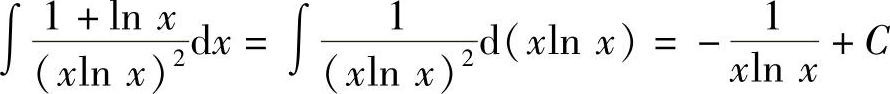
10.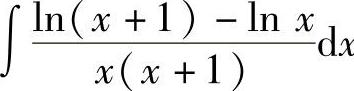 .
.
解
11.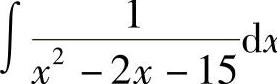 .
.
解
12.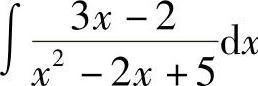 .
.
解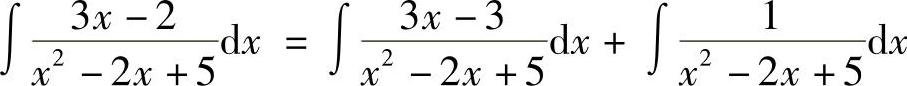
13. .
.
解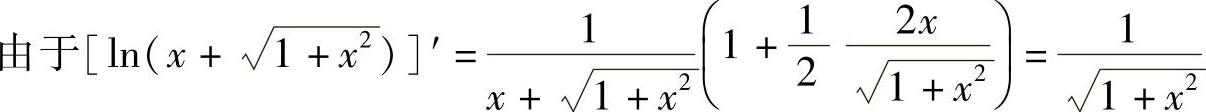 ,故
,故
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






