微积分典例：求平均成本函数和边际成本

1.已知总成本函数C＝C（Ｑ）＝Ｑ³-12Ｑ²+60Ｑ+98，求

（1）平均成本函数及产量为7时的平均成本；

（2）边际成本函数及产量为7时的边际成本.．

解 （1）平均成本函数为

故产量为7时的平均成本为．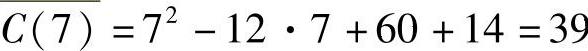

（2）边际成本函数为C′（Ｑ）＝3Ｑ²-24Ｑ+60，故产量为7时的边际成本为C′（7）＝3·7²-24·7+60＝39．

2.已知某产品的总收益函数为Ｒ＝10Ｑ-0.04Ｑ².求

（1）该产品的价格函数和需求函数；

（2）边际收益函数和销量Ｑ＝100时的边际收益；

（3）平均收益函数和销量Ｑ＝100时的平均收益.．

解 （1）由于PＱ＝Ｒ＝10Ｑ-0.04Ｑ²，因此该产品的价格函数为

从而需求函数为

（2）边际收益函数为Ｒ′（Ｑ）＝10-0.08Ｑ，故Ｑ＝100时的边际收益为

Ｒ′（100）＝10-0.08·100＝2

（3）平均收益函数为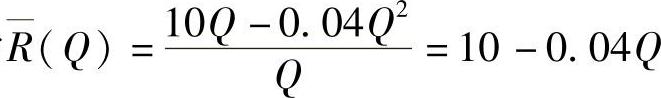，故销量Ｑ＝100时的平均收益为

3.设总收益函数与总成本函数分别为

Ｒ＝Ｒ（Ｑ）＝33Ｑ-4Ｑ²，C＝C（Ｑ）＝Ｑ³-9Ｑ²+36Ｑ+6求利润最大时的产量，产品的价格和利润.．

解 总利润函数为

Ｌ（Ｑ）＝Ｒ（Ｑ）-C（Ｑ）＝33Ｑ-4Ｑ²-（Ｑ³-9Ｑ²+36Ｑ+6）＝-Ｑ³+5Ｑ²-3Ｑ-6

令Ｌ′（Ｑ）＝-3Ｑ²+10Ｑ-3＝0，得Ｑ＝3.因为Ｌ″（3）＝-8＜0，所以当产量为3时利润最大，利润最大时的价格为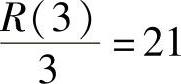，最大利润是Ｌ（3）＝3．

4.一商店按批发价每件4元买进一批商品零售，若零售价每件定为5元，估计可卖出200件，若每件售价每降低0.02元，则可多卖出20件，问商品应买进多少件，每件售价定为多少元时，才可获得最大利润，最大利润是多少？

解　设每件售价定为×，则可卖出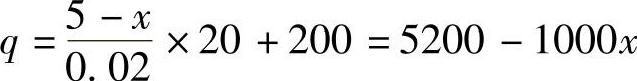件，从而利润函数为

Ｌ（×）＝（5200-1000×）（×-4）

令Ｌ′（×）＝9200-2000×＝0，得×＝4.6.因Ｌ″（4.6）＝-2000＜0，所以当每件售价为4.6元可获得最大利润，此时应买进ｑ＝600件，最大利润是Ｌ（4.6）＝360．(https://www.daowen.com)

5.设某商品的需求函数为Ｑ＝75-P²，试确定价格P，需求Ｑ，以使收益最大.．

解 总收益函数为Ｒ（P）＝Ｑ×P＝（75-P²）P，令Ｒ′（P）＝75-3P²＝0，得P＝5，因Ｒ″（5）＝-6·5＝-30＜0，故当价格为5时可使收益最大，此时需求为Ｑ＝50．

6 设某函数的总成本C（单位：万元）是产量Ｑ（单位：台）的函数为

C＝C（Ｑ）＝0．4Ｑ²+3．8Ｑ+38．4求平均成本最低时的产出水平及最低平均成本．

解 平均成本函数为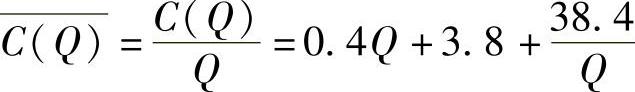，则

令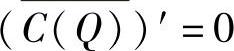，得Ｑ＝9．79．由于是实际问题，故Ｑ的取值只能是整数，故当Ｑ＝10时平均成本最低，最低平均成本为4．

7．求下列函数的弹性．

（1）f（×）＝C （2）f（×）＝A×+B

解 （1）由于f′（×）＝0，所以．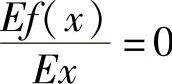

（2）由于f′（×）＝A，所以．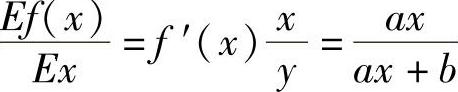

8．设需求函数Ｑ＝100-4P，求

（1）需求价格弹性；

（2）当P＝5，P＝15，P＝12．5时的需求价格弹性，并作经济解释；

（3）当P＝5时的收益价格弹性，并作经济解释．

解 （1）由于Ｑ′＝-4，所以需求价格弹性为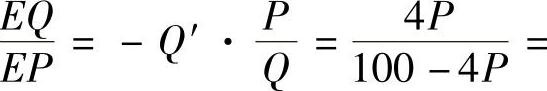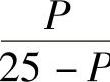P．

（2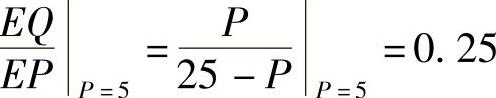），意味着当P＝5时，若价格上涨1％，则需求下跌0．25％；若价格下跌1％，则需求上涨0．25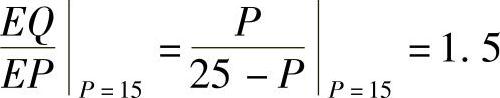％．，意味着当P＝15时，若价格上涨1％，则需求下跌1．5％；若价格下跌1％，则需求上涨1．5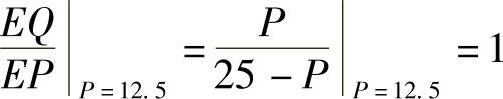％．，意味着当P＝12．5时，若价格上涨1％，则需求下跌1％；若价格下跌1％，则需求上涨1％．

（3）收益函数为Ｒ（P）＝ＱP＝100P-4P²．由于Ｒ′（P）＝100-8P，所以收益价

格弹性为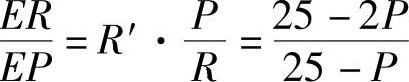，从而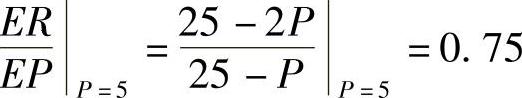．意味着当P＝5时，若价格上涨1％，则收益上涨0．75％；若价格下跌1％，则收益下跌0．75％．

9.设某产品的供给函数Ｑ＝f（P）＝2-2P，

（1）求供给弹性；

（2）求当P＝5时的供给弹性，并作经济解释．

解 （1）由于Ｑ′＝-2，所以供给弹性为；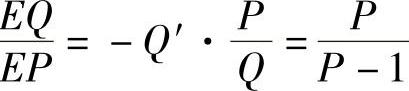

（2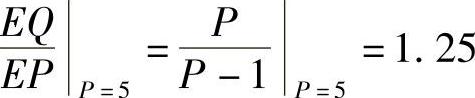），意味着当P＝5时，若价格上涨1％，则供给下跌1．25％；若价格下跌1％，则供给上涨1．25％．