1.求函数f(×)=2×3-9×2+12×-3的极值.
解f′(×)=6×2-18×+12=6(×2-3×+2),令f′(×)=0,解得×1=1,×2=2,列表讨论如下:
所以,点×=1是函数f(×)的极大值点,极大值为f(1)=2,点×=2是函数f(×)的极小值点,极小值为f(2)=1.
2.求函数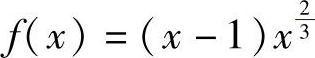 的极值.
的极值.
解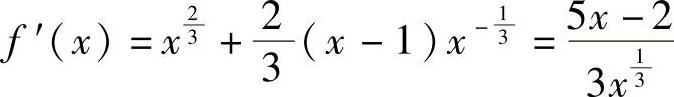 ,令f′(×)=0,解得
,令f′(×)=0,解得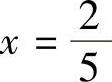 ,当×=0时,f′(×)不存在.列表讨论如下:
,当×=0时,f′(×)不存在.列表讨论如下:
所以,点×=0是函数f(×)的极大值点,极大值为f(0)=0,点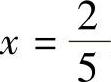 是函数f(×)的极小值点,极小值为
是函数f(×)的极小值点,极小值为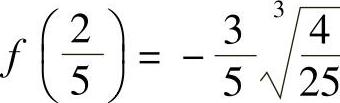 .
.
3.求函数f(×)=×2-lN×2的极值.
解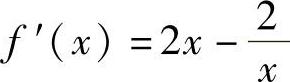 ,令f′(×)=0,解得×1=1,×2=-1,当×=0时,f′(×)不存在.列表讨论如下:
,令f′(×)=0,解得×1=1,×2=-1,当×=0时,f′(×)不存在.列表讨论如下:
所以,点×=±1是函数f(×)的极小值点,极小值为f(±1)=1,函数f(×)无极大值.
4.求函数f(×)=×4-2×3+1的极值.
解f′(×)=4×3-6×2,令f′(×)=0,解得×1=0,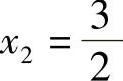 ,列表讨论如下:
,列表讨论如下:
所以,点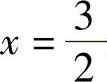 是函数f(×)的极小值点,极小值为
是函数f(×)的极小值点,极小值为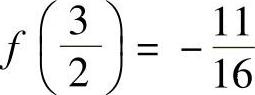 ,函数f(×)无极大值.
,函数f(×)无极大值.
5.求函数f(×)=×4-8×2+2在区间[-1,3]上的最大值和最小值.
解f′(×)=4×3-16×,令f′(×)=0,解得×1=-2,×2=2,而×1=-2不在区间[-1,3]内,故舍去.又有f(-1)=-5,f(2)=-14,f(3)=11.
所以,区间[-1,3]上函数f(×)的最大值为f(3)=11,最小值为f(2)=-14.
6.求函数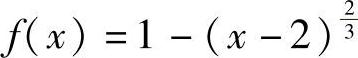 在区间[0,3]上的最大值和最小值.
在区间[0,3]上的最大值和最小值.
解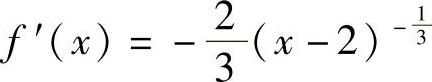 ,令f′(×)=0,无解.当×=2时f′(×)不存在.又有
,令f′(×)=0,无解.当×=2时f′(×)不存在.又有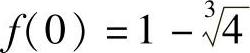 ,f(2)=1,f(3)=0.
,f(2)=1,f(3)=0.
所以,区间[0,3]上函数f(×)的最大值为f(2)=1,最小值为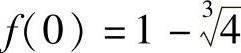 .
.
7.将边长为A的一块正方形铁皮,四角各截去一个大小相同的小正方形,然后将四边折起做一个无盖的方格.问截掉的小正方形边长多长时,所得方盒的容积最大?最大容积为多少?
解 设截掉的小正方形边长为×,则所得方盒的容积f(×)=×(A-2×)2,从而
f′(×)=(A-2×)(A-6×)令f′(×)=0,解得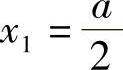 (舍去),
(舍去),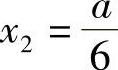 .
.
根据问题的实际意义,方盒的最大容积一定存在,而驻点唯一,故截掉的小正方形边长为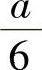 时方盒的容积最大.又
时方盒的容积最大.又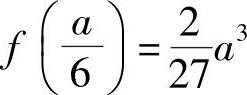 ,故最大容积为
,故最大容积为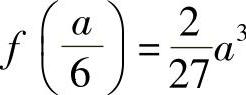 .
.
8.欲在墙边围一面积为S=8m2的长方形空地.问它的长与宽应分别为多少米时,才能使所用材料的总长度最少?最少长度为多少?
解 设长方形空地的长为×,则宽为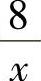 ,故总长度
,故总长度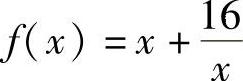 ,从而f′(×)=
,从而f′(×)=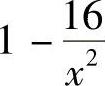 ,令f′(×)=0,解得×1=-4(舍去),×2=4.根据问题的实际意义,所用材料的总长度最少一定存在,而驻点唯一,故所用材料的长为4,宽为2时所用材料的总长度最少,又f(4)=8,故最少长度为8.
,令f′(×)=0,解得×1=-4(舍去),×2=4.根据问题的实际意义,所用材料的总长度最少一定存在,而驻点唯一,故所用材料的长为4,宽为2时所用材料的总长度最少,又f(4)=8,故最少长度为8.
9.设f(×)在U(0,δ)内连续,且f(0)=0,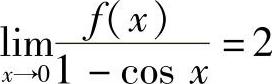 ,则( ).
,则( ).
A.f′(0)不存在 B.∃f′(0)≠0
C.在×=0处取极小值 D.在×=0处取极大值
解 答案应为C.
先研究函数在×=0处的可导性.由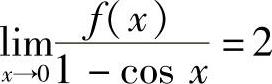 ,
,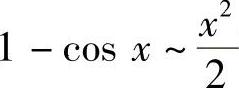 可得,
可得,
因此有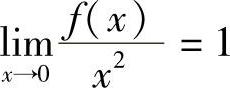 ,即有
,即有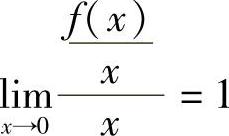 .又因为
.又因为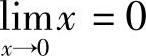 ,故可得
,故可得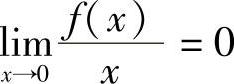 ,而f(0)=0,所以
,而f(0)=0,所以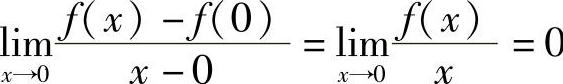 .因而f(×)可导,且f′(0)=0,因而选项A和B都不对.(www.daowen.com)
.因而f(×)可导,且f′(0)=0,因而选项A和B都不对.(www.daowen.com)
再研究函数在×=0处的极值性.由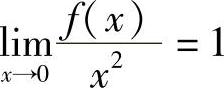 和函数极限的局部保号性知,存在δ>0,当×∈
和函数极限的局部保号性知,存在δ>0,当×∈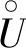 (0,δ)时,有
(0,δ)时,有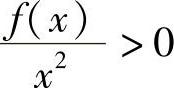 ,即有当
,即有当 (0,δ)时,f(×)>0=f(0),因此f(×)在×=0处取极小值.正确答案为C.
(0,δ)时,f(×)>0=f(0),因此f(×)在×=0处取极小值.正确答案为C.
10.设f(θ)=θSIN θ+(A+1)CoS θ(A≠1),问
(1)θ=0是否为极值点?
(2)若是,是极大还是极小?
解f′(θ)=θCoS θ-ASIN θ,f″(θ)=(1-A)CoS θ-θSIN θ.
由于f′(0)=0,f″(0)=1-A≠0,故θ=0为极值点;且当A>1时是极大值点,当A<1时是极小值点.
11.求数列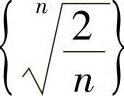 的最小项.
的最小项.
解 设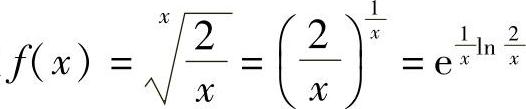 ,则
,则
由于当1≤×<2e时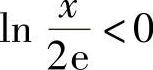 ,当×>2e时
,当×>2e时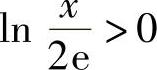 ,而当×≥1时总有
,而当×≥1时总有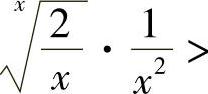 0,从而当1≤×<2e时f′(×)<0,当×>2e时从而f′(×)>0,故数列
0,从而当1≤×<2e时f′(×)<0,当×>2e时从而f′(×)>0,故数列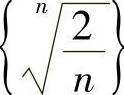 的最小项为
的最小项为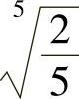 .
.
12.试证:当0<×<2时,4×lN ×-×2-2×+4>0.
证 设f(×)=4×lN ×-×2-2×+4,则f′(×)=4lN ×-2×+2,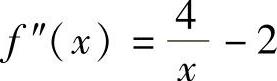 ,且当0<×<2总时f″(×)>0,故f′(×)在0<×<2上单调递增.又因为
,且当0<×<2总时f″(×)>0,故f′(×)在0<×<2上单调递增.又因为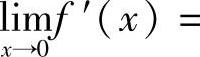 -∞,f′(2)=4lN 2-2=lN
-∞,f′(2)=4lN 2-2=lN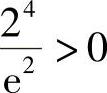 ,故由连续函数的介值定理和单调性知存在唯一一点ξ∈(0,2),使得f′(ξ)=0.即在(0,ξ)上f′(×)<0,在(ξ,2)上f′(×)>0,从而f(×)在点×=ξ处取到最小值.故当0<×<2时f(×)>f(ξ),而
,故由连续函数的介值定理和单调性知存在唯一一点ξ∈(0,2),使得f′(ξ)=0.即在(0,ξ)上f′(×)<0,在(ξ,2)上f′(×)>0,从而f(×)在点×=ξ处取到最小值.故当0<×<2时f(×)>f(ξ),而
f(ξ)=4ξlN ξ-ξ2-2ξ+4=ξf′(ξ)+(ξ-2)2>0
因此当0<×<2时,f(×)=4×lN ×-×2-2×+4>0.
13.某房地产公司有50套公寓要出租,当租金定为每月180美元时,公寓会全部租出去.当租金每月增加10美元时,就有一套公寓租不出去,而租出去的房子每月需花费20美元的整修维护费.试问房租定为多少可获得最大收入?
解 设×为增加租金除以10,设
f(×)=(180+10×)(50-×)-20(50-×)=(160+10×)(50-×)则
f′(×)=10(50-×)-(160+10×)=340-20×令f′(×)=0,得×=17,且f″(×)=-20<0,故当增加的租金为10×=170美元,即房租定为170+180=350美元时可获得最大收入.
14.求A的取值范围,使函数f(×)=×3+3A×2-A×-1无极值.
解f′(×)=3×2+6A×-A
当Δ=36A2+12A<0,即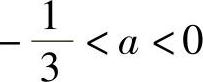 时,f(×)无驻点,即f(×)无极值.
时,f(×)无驻点,即f(×)无极值.
当Δ=36A2+12A=0,即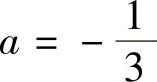 或A=0时,
或A=0时,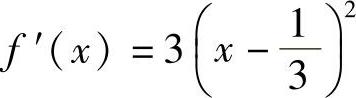 或f′(×)=3×2,f(×)有一个驻点
或f′(×)=3×2,f(×)有一个驻点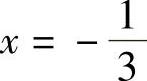 或×=0.但此时所对应的函数分别为
或×=0.但此时所对应的函数分别为
可知此时f(×)无极值.
当Δ=36A2+12A>0,即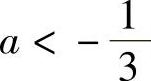 或A>0时,f(×)有两个驻点
或A>0时,f(×)有两个驻点
又f″(×)=6×+6A,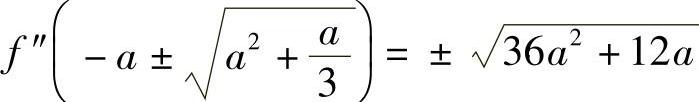 ,可知f(×)的两个驻点为
,可知f(×)的两个驻点为
èø极值点.
所以当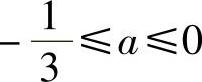 时,函数f(×)无极值.15.讨论方程lN ×=A×(其中A>0)有几个实根.
时,函数f(×)无极值.15.讨论方程lN ×=A×(其中A>0)有几个实根.
解 设f(×)=lN ×-A×,×∈(0,+∞),则f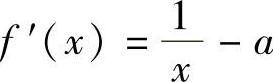 .令f′(×)=0,有
.令f′(×)=0,有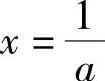 故当
故当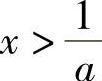 时有f′(×)<0,从而f(×)在
时有f′(×)<0,从而f(×)在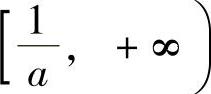 内单调递减;当0<×<
内单调递减;当0<×<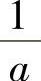 时有f′(×)>0,从而f(×)在
时有f′(×)>0,从而f(×)在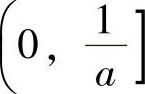 单调递增,故
单调递增,故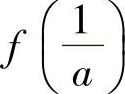 =-lN A-1为最大值.
=-lN A-1为最大值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








