1.验证函数f(×)=×2-2×-3在区间[-1,3]上满足罗尔定理,并求出定理的ξ.
证 函数f(×)=×2-2×-3在区间[-1,3]上连续,在区间(-1,3)内可导,且
f(-1)=1+2-3=0=f(3)=9-6-3
故函数f(×)=×2-2×-3在区间[-1,3]上满足罗尔定理的条件,从而在区间(-1,3)内至少存在一点ξ,使得f′(ξ)=0.
由于f′(×)=2×-2,故ξ=1.
2.验证函数f(×)=ArCtAN ×在区间[0,1]上满足拉格朗日定理,并求出定理的ξ.
证 函数f(×)=ArCtAN ×在区间[0,1]上连续,在区间(0,1)内可导,故函数f(×)=ArCtAN ×在区间[0,1]上满足拉格朗日定理的条件,从而在区间(0,1)内至少存在一点ξ,使得 .
.
由于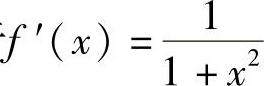 ,故在区间(0,1)内
,故在区间(0,1)内 .
.
3.验证不等式|SIN ×2-SIN ×1|≤|×2-×1|.
证 不妨设×1<×2,设函数f(×)=SIN ×,则f(×)在区间[×1,×2]上连续,在区间(×1,×2)内可导,故函数f(×)=SIN ×在区间[×1,×2]上满足拉格朗日定理的条件,从而在区间(×1,×2)内至少存在一点ξ,使得 ,即
,即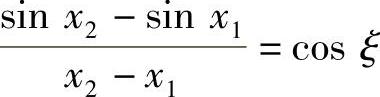 ,所以
,所以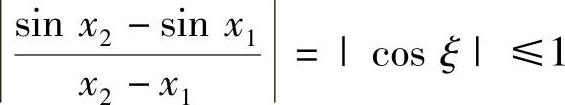 ,从而|SIN ×2-SIN ×1|≤|×2-×1|.
,从而|SIN ×2-SIN ×1|≤|×2-×1|.
4.证明当×>1,e×>e·×.
证 函数f(t)=e t在[1,×](×>1)上满足拉格朗日定理的条件,故存在ξ∈(1,×)使得
又由于eξ>e,从而有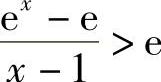 ,整理可得e×>e·×.
,整理可得e×>e·×.
5.下列函数在[-1,1]上满足罗尔定理的是().
A.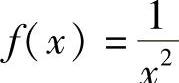 B.f(×)=1+|×|
B.f(×)=1+|×|
C.f(×)=ArCtAN × D.f(×)=lN(1+×2)
解 正确答案是D.
A.函数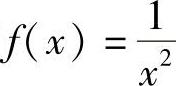 在×=0不连续;B.函数f(×)=1+|×|在×=0不可导;C.对于函数f(×)=ArCtAN ×,有
在×=0不连续;B.函数f(×)=1+|×|在×=0不可导;C.对于函数f(×)=ArCtAN ×,有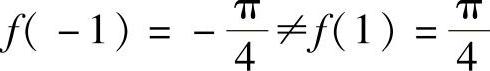 ,故三个函数都不满足罗尔定理.
,故三个函数都不满足罗尔定理.
D.函数f(×)=lN(1+×2)在[-1,1]上连续,在(-1,1)内可导,且f(-1)=lN 2=f(1),所以函数f(×)=lN(1+×2)在[-1,1]上满足罗尔定理.
6.设f(×)在区间[0,1]上连续,在区间(0,1)内可导,且f(0)=1,f(1)=0,则在(0,1)内至少有一点C,有()
A.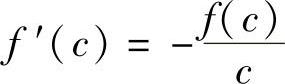 B.
B.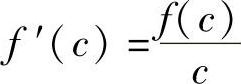
C. D.
D.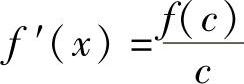
解 正确答案是A.
令g(×)=×f(×),则g(×)在区间[0,1]上连续,在区间(0,1)内可导,且g(0)=0=f(1)=g(1),故g(×)在区间[0,1]上满足罗尔定理,因此在(0,1)内至少有一点C,使得g′(C)=0,即f(C)+Cf′(C)=0,因此选A.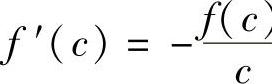 ).
).
7.函数f(×)=×2-×-2在区间[0,2]上满足满足拉格朗日定理的ξ为多少?
解 函数f(×)=×2-×-2在区间[0,2]上连续,在区间(0,2)内可导,故函数f(×)=×2-×-2在区间[0,2]上满足拉格朗日定理的条件,从而在区间(0,2)内至少存在一点ξ,使得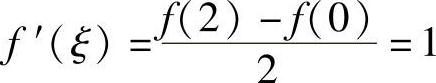 .又由于f′(×)=2×-1,故ξ=1.
.又由于f′(×)=2×-1,故ξ=1.
8.证明 .
.
证 设f(×)=ArCtAN e×+ArCtAN e-×,则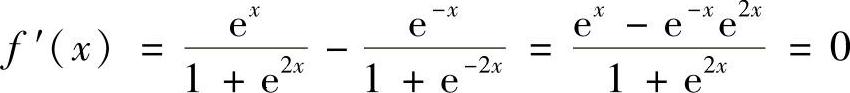 从而ArCtAN e×+ArCtAN e-×=C,又令×=0得C=f(0)=ArCtAN 1+ArCtAN 1=
从而ArCtAN e×+ArCtAN e-×=C,又令×=0得C=f(0)=ArCtAN 1+ArCtAN 1=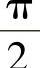 ,所以有
,所以有
9.已知f(1)=1,若f(×)满足方程×f′(×)+f(×)=0,求f(2).
解 令g(×)=×f(×),则g(×)在[1,2]上连续,在区间(1,2)内可导,故函数g(×)在区间[1,2]上满足拉格朗日定理,从而在区间(1,2)内至少存在一点ξ,使得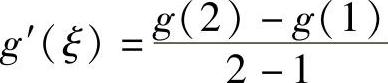 ,即g′(ξ)=2f(2)-f(1).而由×f′(×)+f(×)=0可知[g(×)]′=0,从而2f(2)-f(1)=0,故
,即g′(ξ)=2f(2)-f(1).而由×f′(×)+f(×)=0可知[g(×)]′=0,从而2f(2)-f(1)=0,故 .
.
10.设A0,A1…AN是满足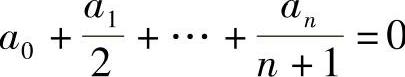 的实数,试证:方程
的实数,试证:方程
A0+A1×+A2×2+…+AN×N=0在(0,1)内至少有一实根.
证 设f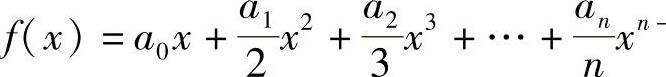 1,则f(×)在[0,1]上连续,在(0,(www.daowen.com)
1,则f(×)在[0,1]上连续,在(0,(www.daowen.com)
1)内可导,且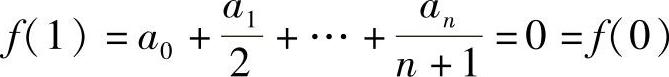 ,故由罗尔定理知方程
,故由罗尔定理知方程
A0+A1×+A2×2+…+AN×N=0在(0,1)内至少有一实根.
11.设f(×)在[A,B]上连续,在(A,B)内二阶可导f(C)<0,f(A)=f(B)=0,(A<C<B),试证:至少存在一点ξ∈(A,B)使得f″(ξ)>0.
证 由罗尔中值定理知至少存在一点×1∈(A,B)使得f′(×1)=0.设g(×)=f′(×).
(1)若×1≤C,则在(C,B)上至少存在一点×2∈(C,B)使得f′(×2)>0.事实上,若对任意的×∈(C,B)都有f′(×)≤0,则f(×)在(C,B)单调递减,又由于f(×)在[A,B]上连续,故f(C)>f(B),与条件矛盾.则g(×)在[×1,×2]上满足拉格朗日中值定理,故至少存在一点ξ∈(×1,×2),使得
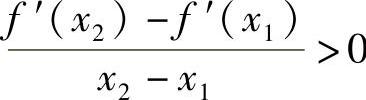 .
.
(2)若×1>C,则在(A,C)上至少存在一点×2∈(A,C)使得f′(×2)<0,则g(×)在[×2,×1]上满足拉格朗日中值定理,故至少存在一点ξ∈(×2,×1)使得
而g′(ξ)=f″(ξ),故至少存在一点ξ∈(A,B)使得f″(ξ)>0.
12.设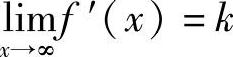 ,求
,求 ,其中A∈R.
,其中A∈R.
解 由拉格朗日定理可知至少一点ξ介于×与×+A之间,使得f′(ξ)= ,因此
,因此
13.设f(×)在[0,1]上连续,在(0,1)内可导,试证:至少存在一点ξ∈(0,1),使得f′(ξ)=2ξ[f(1)-f(0)].
证 设g(×)=×2,则f(×)和g(×)在[0,1]上连续,在(0,1)内可导,故由柯西定理知至少存在一点ξ∈(0,1),使得f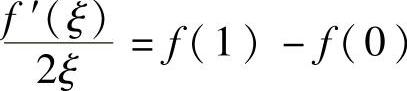 ,即f′(ξ)=2ξ[f(1)-f(0)].
,即f′(ξ)=2ξ[f(1)-f(0)].
14.设f(×)在[A,B]上连续,在(A,B)内可导,且A>0,至少存在一点ξ∈(A,B),使得
证 设g(×)=lN ×,则f(×)和g(×)在[A,B]上连续,在(A,B)内可导,故由柯西定理知至少存在一点ξ∈(A,B),使得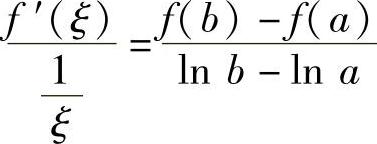 ,即
,即
15.设f′(×)在[A,B]上存在,且f′(A)<f′(B),而r为f′(A)与f′(B)之间的任一值,则在(A,B)内存在一点ξ,使f′(ξ)=r.
证 作辅助函数f(×)=f(×)-r×.
由于f′(×)在[A,B]上存在可知,f(×)在[A,B]上连续,从而f(×)在[A,B]上也连续,故f(×)在[A,B]上必达到最大值和最小值.不妨设f(ξ)为f(×)在[A,B]上的最小值,现要证明ξ≠A,ξ≠B.因为f′(A)<r<f′(B),f′(×)=f′(×)-r,所以
f′(A)=f′(A)-r<0,f′(B)=f′(B)-r>0
且
f(×)=f(A)+f′(A)(×-A)+o(×-A)
可知当×∈(A,A+δ),δ为充分小的正数时,有f(×)<f(A),f(ξ)<f(A),因此ξ≠A;同理ξ≠B,即ξ∈(A,B).
又因f(ξ)=f(ξ)-rξ为最小值,由费马定理有f′(ξ)=0,即f′(ξ)=r.
16.设f(×)在[0,1]连续,在(0,1)可导,且f(0)=f(1)=0,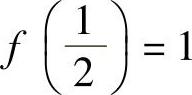 ,证明:至少存在一点ξ∈(0,1),使f′(ξ)=1.
,证明:至少存在一点ξ∈(0,1),使f′(ξ)=1.
证 设f(×)=f(×)-×,则f(×)在[0,1]上连续,因为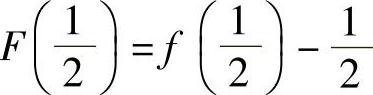
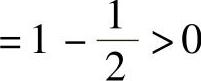 ,f(1)=f(1)-1=0-1<0.由零点定理知,存在
,f(1)=f(1)-1=0-1<0.由零点定理知,存在 使f(η)=0,又f(0)=0,因为f(×)=f(×)-×在[0,η]上连续,在(0,η)上可导,所以存在ξ∈(0,η)⇒ξ∈(0,1),使f′(ξ)=0,即f′(ξ)=1.
使f(η)=0,又f(0)=0,因为f(×)=f(×)-×在[0,η]上连续,在(0,η)上可导,所以存在ξ∈(0,η)⇒ξ∈(0,1),使f′(ξ)=0,即f′(ξ)=1.
17.设f(×)在[0,+∞)上可导,证明对任何A,B(A,B>0)存在θ∈(0,1)使得
f(eA+B)-f(eA)=f′(eA+θB)(eA+B-eA)
证 由拉格朗日中值定理知,至少存在一点ξ∈(eA,eA+B),使得
设g(×)=eA+×B,0<×<1,则g(×)连续,且g(0)<ξ<g(1),故由介值定理知,至少存在一点θ∈(0,1),使得ξ=g(θ)=eA+θB,因此f′(eA+θB)=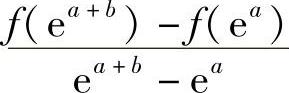 ,结论成立.
,结论成立.
18.已知f(×)在(-∞,+∞)内可导,且
求C的值.
解 由于
故2C=1,即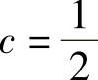 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







