1.计算函数y=×2在×=1,Δ×=0.01时函数的改变量Δy与微分Dy.
解 Δy=(×+Δ×)2-×2=1.012-12=1.0201-1=0.0201Dy=y′D××=1=2×D××=1=2·0.01=0.02
2.求下列函数的微分.
(1)y=e×SIN× (2)y=ArCtAN×2
(3)y=SIN(3×+1) (4)y=lN(1+e×2)
解 (1)Dy=(e×SIN×)′D×=(e×SIN×+e×CoS×)D×=e×(SIN×+CoS×)D×
(2)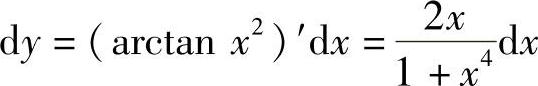
(3)Dy=[SIN(3×+1)]′D×=3CoS(3×+1)D×
(4)
3.求下列函数的微分.
(1)y=e×lN×2+SIN× (2)y=eA×+B×2
解 (1)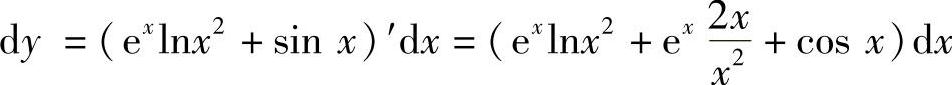
(2)Dy=(eA×+B×2)′D×=eA×+B×2(A+2B×)D×
4.设ySIN×-CoS(×-y)=0,求Dy.
解 方程两端对×求导数,有
y′SIN×+yCoS×+SIN(×-y)(1-y′)=0
从而有
所以 .(https://www.daowen.com)
.(https://www.daowen.com)
5.在下列括号中填入适当的函数使等式成立.
(1)D()=×D×(2)D()=CoSωtDt
解 (1)由于 ,所以
,所以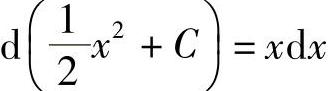 .
.
(2)由于 ,所以
,所以 .
.
6.求SIN29°的近似值.
解 令f(×)=SIN×, ,
,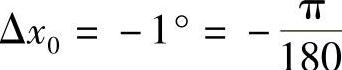 ,又f′(×)=CoS×,故
,又f′(×)=CoS×,故
7.有一批半径为1Cm的球,为了提高球面的光洁度,要镀上一层铜,厚度定为0.01Cm,估计一下,每只球需要铜多少克?(铜的密度为8.9g/Cm3)
解 令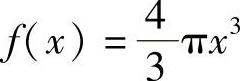 ,×0=1Cm,Δ×0=0.01Cm,又f′(×)=4π×2,故
,×0=1Cm,Δ×0=0.01Cm,又f′(×)=4π×2,故
Δy≈f′(×0)Δ×=4π×2×0=1·0.01=0.1256Cm3
因此Δy·m=0.1256·8.9=1.11784g,即每只球需要铜1.11784克.
8.已知 ,求f(×).
,求f(×).
解 由于
故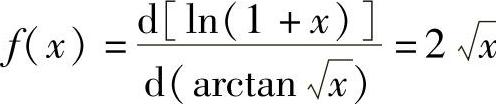 .
.
9.设y=f(×)在×0点可导,当×由×0增至×0+Δ×时, =( ).
=( ).
A.0 B.1 C.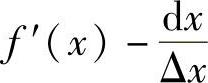 D.不存在
D.不存在
解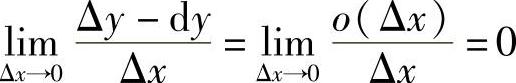 ,故正确答案是A.
,故正确答案是A.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





