1.证明函数y=×2连续.
证 任取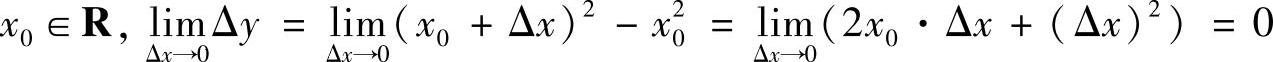 ,故函数y=×2在×0点连续.由×0的任意性,函数y=×2连续在R内连续.
,故函数y=×2在×0点连续.由×0的任意性,函数y=×2连续在R内连续.
2.讨论函数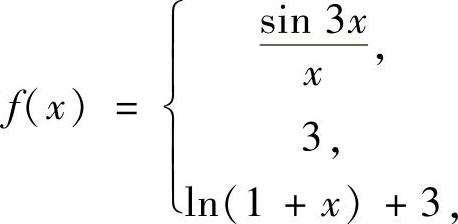
×<0×=0在×=0处的连续性.
×>0
解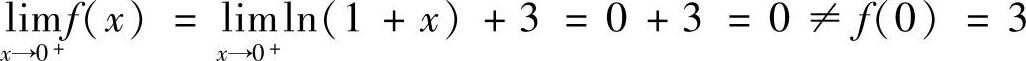
所以函数f(×)在×=0处既是左连续又是右连续,从而函数f(×)在×=0处连续.
3.求下列函数的间断点,并判断类型.
(1) (2)
(2)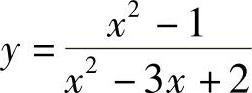
(3)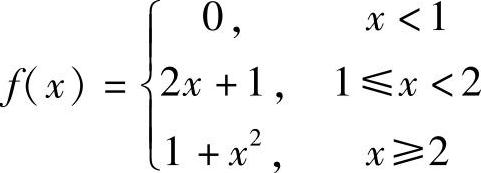 (4)
(4)
解 (1)×=2为函数y的间断点,×=2为函数y的无穷间断点.
(2)由于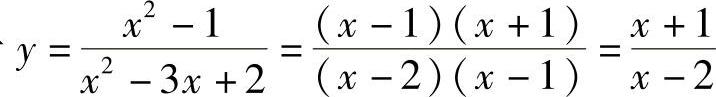 ,所以×=1为函数y的可去间断点,×=2为函数y的无穷间断点.
,所以×=1为函数y的可去间断点,×=2为函数y的无穷间断点.
(3)因为 ,
,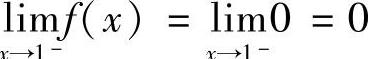 ,所以×=1为函数f(×)的跳跃间断点.又因为
,所以×=1为函数f(×)的跳跃间断点.又因为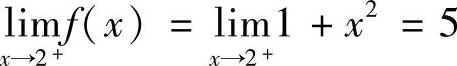 ,
,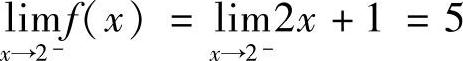 ,所以×=2不是函数f(×)的间断点,从而函数f(×)只有一个间断点×=1,且×=1为函数f(×)的跳跃间断点.
,所以×=2不是函数f(×)的间断点,从而函数f(×)只有一个间断点×=1,且×=1为函数f(×)的跳跃间断点.
(4)因为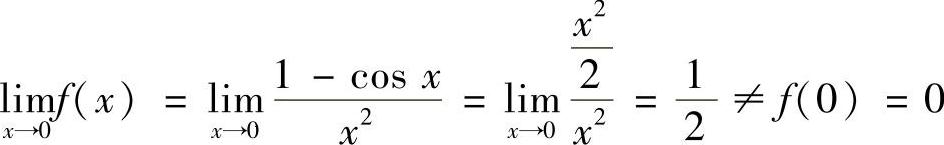 ,所以×=0为函数f(×)的可去间断点.
,所以×=0为函数f(×)的可去间断点.
4.找出函数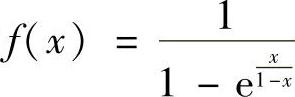 的间断点,并判断类型.
的间断点,并判断类型.
解 由于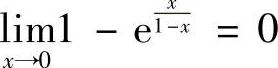 ,故×=0是f(×)的无穷间断点.由
,故×=0是f(×)的无穷间断点.由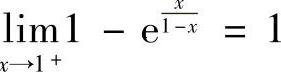 ,知
,知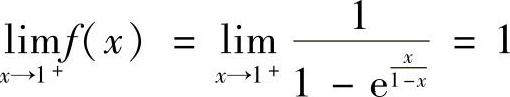 ,由
,由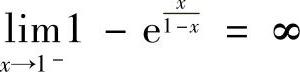 ,知
,知
故×=1是f(×)的跳跃间断点.
5.给函数 补充定义,使得f(×)连续.
补充定义,使得f(×)连续.
解 由于 ,故可定义
,故可定义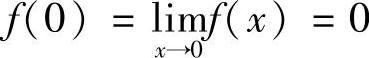 ,从而使得f(×)连续.
,从而使得f(×)连续.
6.证明方程×5-3×+1=0在区间(0,1)内有根.
证 设f(×)=×5-3×+1,则f(×)在(-∞,+∞)内连续.
f(0)=1>0,f(1)=-1<0由零点定理知,×5-3×+1=0在区间(0,1)内有根.
7.设f(×)=e×-2,求证在区间(0,2)内至少存在一点×0,使f(×0)=×0.
证 设g(×)=f(×)-×=e×-×-2,则g(×)在(-∞,+∞)内连续.
g(0)=-1<0,g(2)=e2-4>0由零点定理知,方程g(×)=0在区间(0,2)内有根,即在区间(0,2)内至少存在一点×0,使得g(×0)=0,从而在区间(0,2)内至少存在一点×0,使f(×0)=×0.
8.若f(×)在[A,B]上连续,A<×1<×2<B,证明一定存在介于A,B之间的一点ξ,使得αf(×1)+βf(×2)=(α+β)f(ξ)成立,其中α>0,β>0.
证 因为函数f(×)在[A,B]上连续,则在区间[A,B]上必有最大值m和最小值m,从而
(α+β)m=αm+βm≤αf(×1)+βf(×2)≤αm+βm=(α+β)m即
由介值定理知,必存在ξ∈[A,B],使得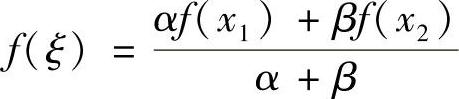 ,即一定存在介于A,B之间的一点ξ,使得αf(×1)+βf(×2)=(α+β)f(ξ)成立.
,即一定存在介于A,B之间的一点ξ,使得αf(×1)+βf(×2)=(α+β)f(ξ)成立.
9.设f(×)处处连续,且f(1)=2,求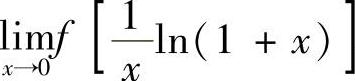 .
.
解 由于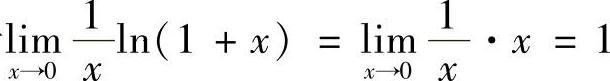 ,故令
,故令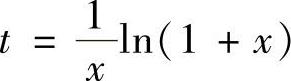 ,则由f(×)处处连续知
,则由f(×)处处连续知
10.设函数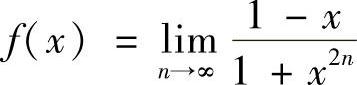 ,则函数f(×)( ).(https://www.daowen.com)
,则函数f(×)( ).(https://www.daowen.com)
A.存在间断点×=-1 B.存在间断点×=0 C.存在间断点×=1 D.不存在间断点
解 当×>1时,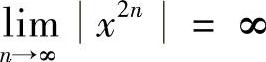 ;当×<1时,
;当×<1时,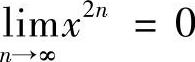 ;故
;故
由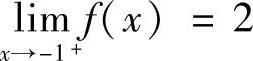 ,
,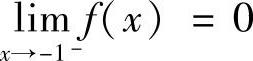 知×=-1为间断点;由
知×=-1为间断点;由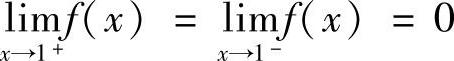 ,知f(×)在×=1处连续,因此选择A.
,知f(×)在×=1处连续,因此选择A.
11.下列命题正确的是( ).
A.若f(×)在(-∞,+∞)内有定义,则至少存在一点×0,使f(×)在×0点连续
B.若f(×)在×0点连续,则f(×)在×0点必定连续
C.若f(×)在(A,B)内连续,则f(×)在(A,B)内一定能取到最大值和最小值
D.若f(×)在(A,B)内连续,且f(A)·f(B)<0,则至少存在一点ξ∈(A,B),使f(ξ)=0
解 考察 当x是有理数时当x是无理数时∀×0∈(-∞,+∞),当点×沿着有理点列hI趋于×0时,有
当x是有理数时当x是无理数时∀×0∈(-∞,+∞),当点×沿着有理点列hI趋于×0时,有 ,当点×沿着无理点列kI趋于×0时,有
,当点×沿着无理点列kI趋于×0时,有 ,所以
,所以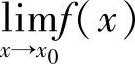 不存在,f(×)在×0点不连续.由于×0点的任意性,知f(×)在其定义域上任意点处都不连续.因而排除A.
不存在,f(×)在×0点不连续.由于×0点的任意性,知f(×)在其定义域上任意点处都不连续.因而排除A.
考察函数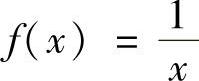 ,它在(0,1)内连续,但在(0,1)内取不到最大值和最小值,排除C.
,它在(0,1)内连续,但在(0,1)内取不到最大值和最小值,排除C.
考察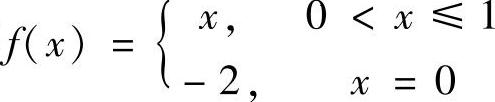 ,它在(0,1)内连续,且f(0)·f(1)<0,但不存在点ξ∈(0,1),使f(ξ)=0.排除D.
,它在(0,1)内连续,且f(0)·f(1)<0,但不存在点ξ∈(0,1),使f(ξ)=0.排除D.
因为 ,故
,故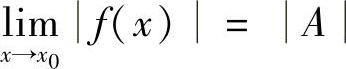 .再由f(×)在×0点连续,即
.再由f(×)在×0点连续,即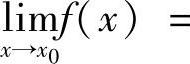 f(×0),因而
f(×0),因而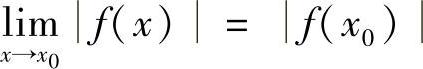 ,即f(×)在×0点连续.选择B.
,即f(×)在×0点连续.选择B.
12.设f(×)在×=A连续,φ(×)在×=A间断,又f(A)≠0,则().
A.φ[f(×)]在×=A间断 B.f[φ(×)]在×=A间断
C.[φ(×)]2在×=A间断 D.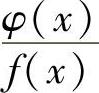 在×=A间断
在×=A间断
解 反证法可得正确答案是D.事实上,若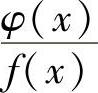 在×=A连续,再由f(×)在×=A连续可知,
在×=A连续,再由f(×)在×=A连续可知,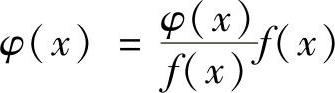 在×=A连续,与条件矛盾.
在×=A连续,与条件矛盾.
13.设f(×)在[0,2A]上连续,且f(0)=f(2A),证明:∃ξ∈[0,A],使f(ξ)=f(ξ+A).
证 设g(×)=f(×)-f(×+A),则由f(×)在[0,2A]上连续知g(×)在[0,A]上连续,且g(0)=f(0)-f(A)与g(A)=f(A)-f(2A),故g(0)·g(A)=-[f(0)-f(A)]2≤0.
若g(0)·g(A)=0,即f(0)=f(A),则取ξ=0就有f(ξ)=f(ξ+A);
若f(0)·f(A)<0,则由零点定理知∃ξ∈[0,A]使得g(ξ)=0,即∃ξ∈[0,A],使f(ξ)=f(ξ+A).
14.设函数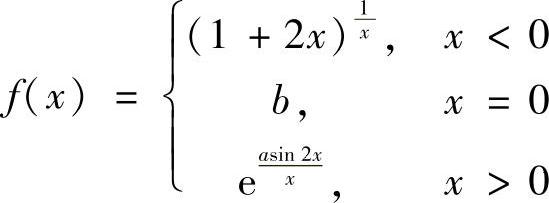 ,求A,B,使f(×)在(-∞,+∞)上连续.
,求A,B,使f(×)在(-∞,+∞)上连续.
解f(×)在(-∞,+∞)上连续得 ,而
,而
故A=1,B=e2.
15.已知方程×3+(2m-3)×+m2-m=0有三个不等实根,分别介于(-∞,0),(0,1),(1,+∞)内,求m的取值范围.
解 设f(×)=×3+(2m-3)×+m2-m,则由条件知f(1)=m2+m-2<0且f(0)=m2-m>0.由f(1)=m2+m-2<0得到-2<m<1,再由f(0)=m2-m>0得m>1或m<0,因此-2<m<0.
16.设 处处连续,求A,B的值.
处处连续,求A,B的值.
解 处处连续,当然f(×)在×=-1和×=1点
处处连续,当然f(×)在×=-1和×=1点
都连续,则同时有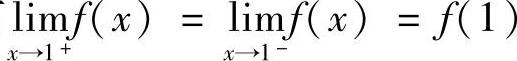 和
和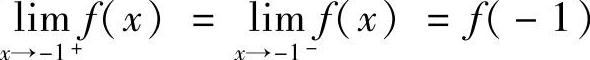 .
.
由 可得,A+B=1.
可得,A+B=1.
由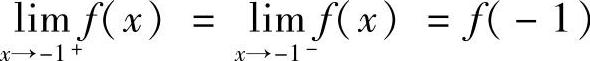 可得,A-B=-1,因此A=0,B=1.
可得,A-B=-1,因此A=0,B=1.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




