1.直观判断下列变量,当×→?时是无穷小;当×→?时是无穷大:(1)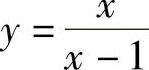 (2)y=lN(1+×)
(2)y=lN(1+×)
解 (1)当×→0时,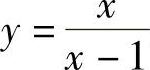 是无穷小;当×→1时,
是无穷小;当×→1时,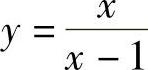 是无穷大.
是无穷大.
(2)当×→0时,y=lN(1+×)是无穷小;当×→-1和×→+∞时,y=lN(1+×)是无穷大.
2.当×→0时,将下列无穷小与无穷小×进行阶的比较.
(1)tAN ×-SIN × (2)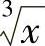 (3)
(3)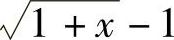 (4)lN(1+2×)
(4)lN(1+2×)
解 (1)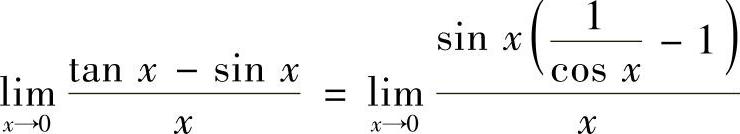
所以当×→0时,tAN ×-SIN ×是×的高阶无穷小.
(2)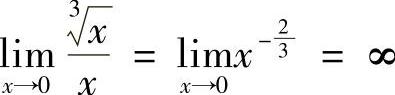 ,所以当×→0时,
,所以当×→0时,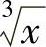 是×的低阶无穷小.
是×的低阶无穷小.
(3)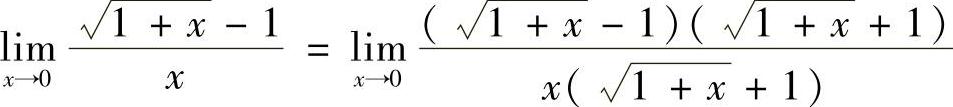
所以当×→0时,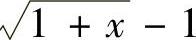 是×的同阶无穷小.
是×的同阶无穷小.
(4)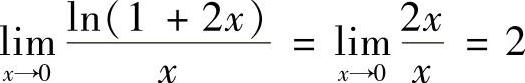 ,所以当×→0时,lN(1+2×)是×的同阶无穷小.
,所以当×→0时,lN(1+2×)是×的同阶无穷小.
3.证明:当×→0时,e×-1与×是等价无穷小.证 令y=e×-1,则×=lN(1+y),从而有
故当×→0时,e×-1与×是等价无穷小.
4.用等价无穷小代换求极限.
(1)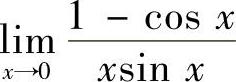 (2)
(2)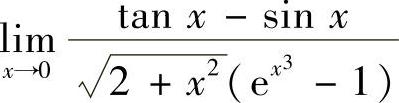
(3)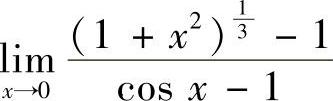
解 (1)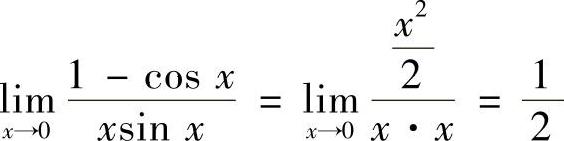
(2)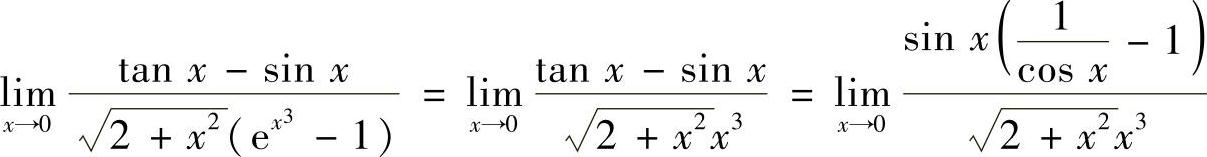
(3)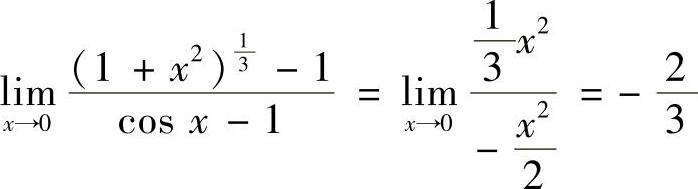
5.下列等式成立的有( ).
A.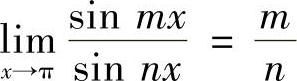 B.
B.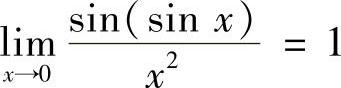
C.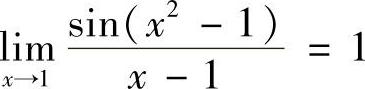 D.
D.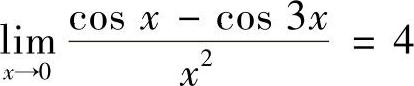
解 正确答案是D.
选项A不能用等价无穷小代换,故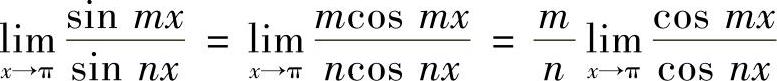 ,而由于极限
,而由于极限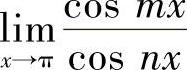 与m,N的取值有关,可能为±1,从而极限
与m,N的取值有关,可能为±1,从而极限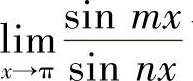 可能为
可能为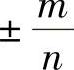 ,故A不正确.
,故A不正确.
由等价无穷小代换知
因此B和C也不正确.
而
故选项D是正确的 .(https://www.daowen.com)
6. 当×→0时,与×为等价无穷小量的是( ).
A.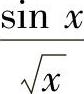 B.
B.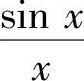 C.
C.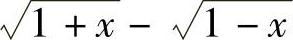 D.
D.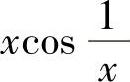
解 正确答案是C.
因为由等价无穷小代换知
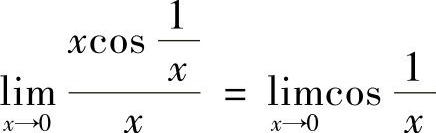 不存在,故正确答案是C.
不存在,故正确答案是C.
7.设当×→0时,(1-CoS ×)lN(1+×2)是比×SIN ×N高阶的无穷小,而×SIN ×N是比e×2-1高阶的无穷小,则正整数N等于().
A.0 B.1 C.2 D.3
解 正确答案是C.
由(1-CoS ×)lN(1+×2)是比×SIN ×N高阶的无穷小知
从而知N<3;
由×SIN ×N是比e×2-1高阶的无穷小知
从而知N>1.故正整数N等于2.
8.求极限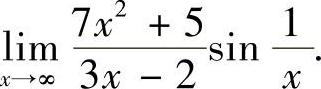
解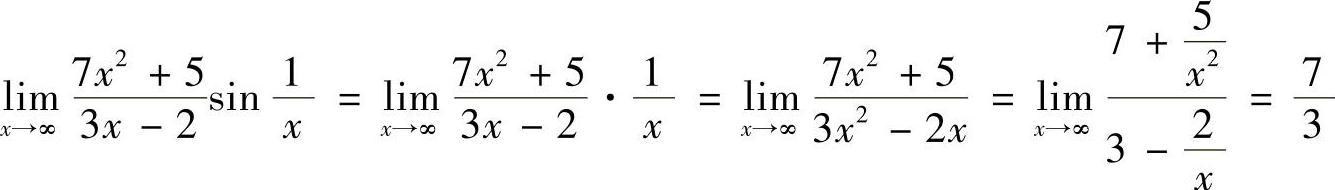
9.若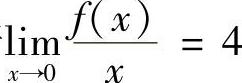 ,求
,求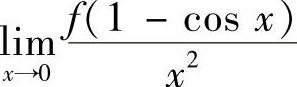 .
.
解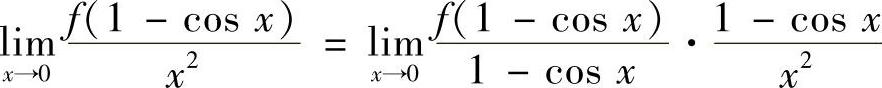
10.求极限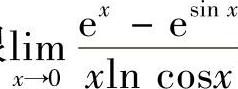 .
.
解 由于×→0时,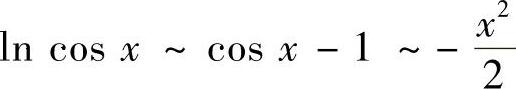 ,故
,故
11.当×→0时,与×等价的无穷小量是( ).
A.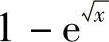 B.
B.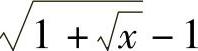 C.
C.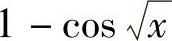 D.
D.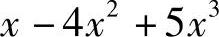
解 由于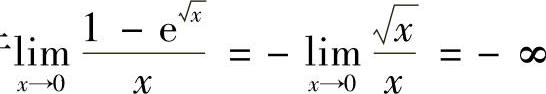
故当×→0时,与×等价的无穷小量是D:×-4×2+5×3.
12.已知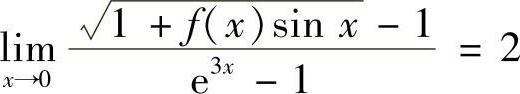 ,求
,求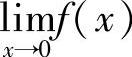 .
.
解 由于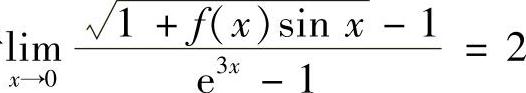 且
且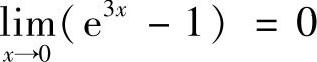 ,故
,故
从而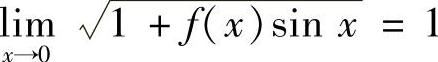 ,故
,故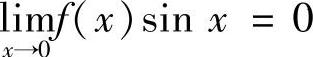 ,所以有
,所以有
再由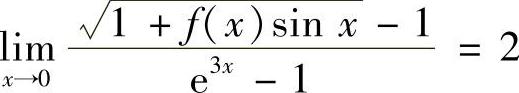 得,
得,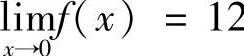 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






