1.求极限.
(1)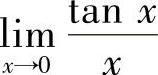 (2)
(2)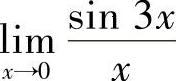 (3)
(3)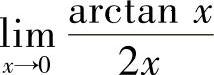
(4)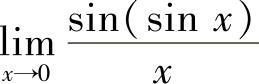 (5)
(5)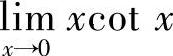 (6)
(6)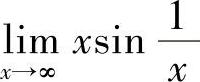
解 (1)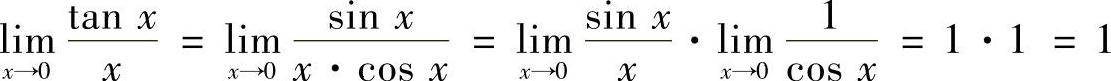
(2)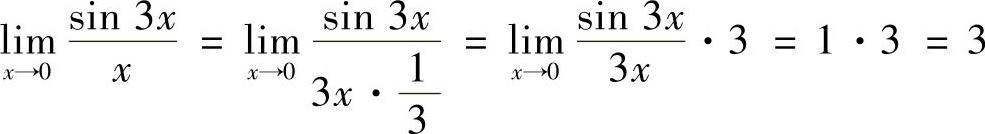
(3)令t=ArCtAN ×,则
(4)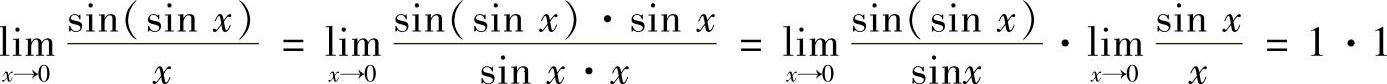 =1
=1
(5)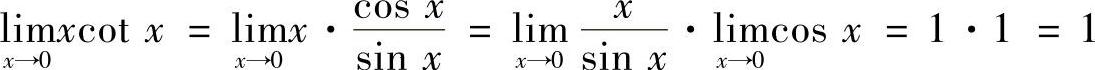
2.求极限.
(1)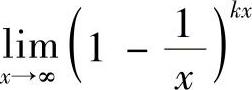 (2)
(2)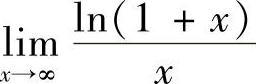 (3)
(3)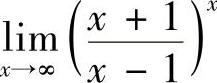
(4)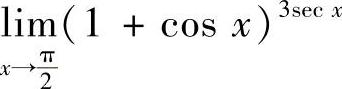
解 (1)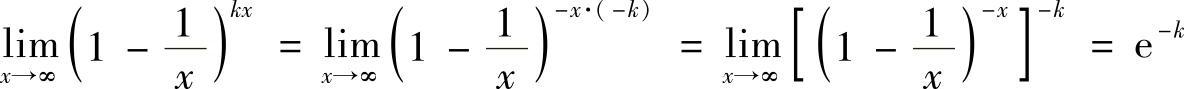
(2)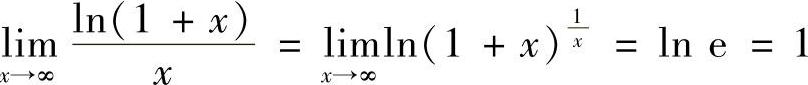
(3)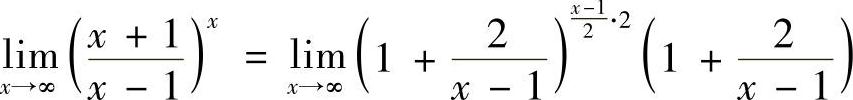
(4)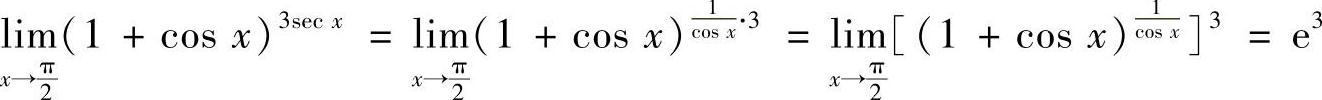
3.设0<×1<1,N=1,2,…,×N+1=2×N-×2N,证明数列{×N}的极限存在,并求其极限.
证 由×N+1=2×N-×2N可知,×2=2×1-×21=1-(1-×1)2,从而0<×2<1,由数学归纳法可知0<×N<1,即数列{×N}有界.
由×N+1=2×N-×2N可知,×N+1=×N(2-×N),再由0<×1<1得
×2=×1(2-×1)>×1由归纳法可知,数列{×N}是单调递增数列.由单调有界原理知,数列{×N}极限存在.由于数列{×N}极限存在,不妨设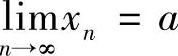 ,故对等式×N+1=2×N-×2N取极限,得A=2A-A2,得A=0,1,再由数列的递增性可知A>×1>0,从而得A=1.
,故对等式×N+1=2×N-×2N取极限,得A=2A-A2,得A=0,1,再由数列的递增性可知A>×1>0,从而得A=1.
4.下列极限中正确的是( ).
A.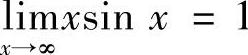 B.
B.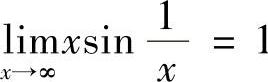
C.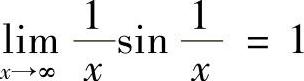 D.
D.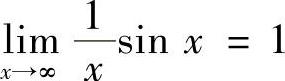
解 正确答案是B.因为由第一个重要极限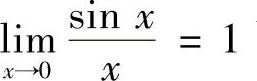 可知,
可知,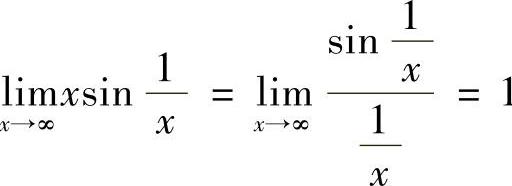 .
.
5.设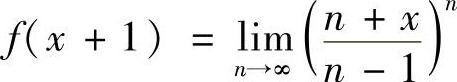 ,求f(×).
,求f(×).
解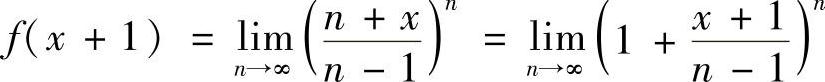
所以f(×)=e×+1.
6. 若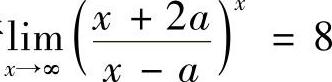 ,求A.
,求A.
解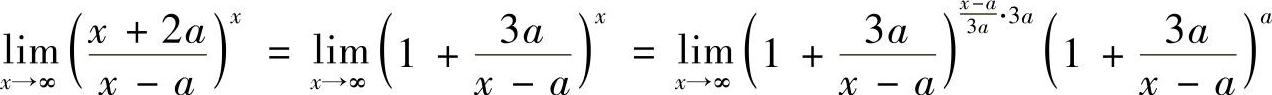
又由于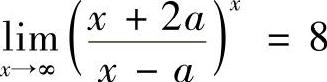 ,即e3A=8,故A=lN 2.
,即e3A=8,故A=lN 2.
7.求极限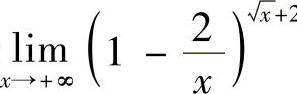 .
.
解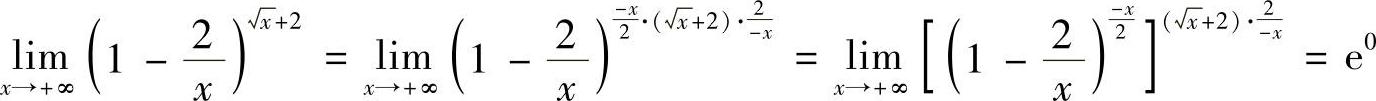 =1
=1
8.求极限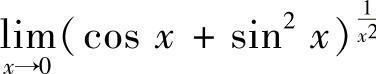 .(https://www.daowen.com)
.(https://www.daowen.com)
解 令u(×)=CoS ×+SIN2×,v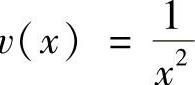 ,则
,则
故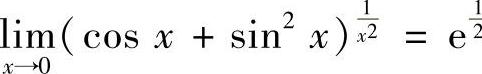 .
.
9.证明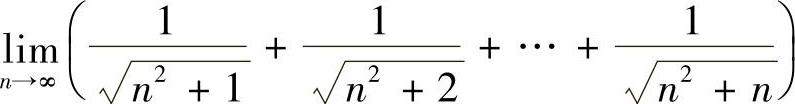 存在,并求其值.
存在,并求其值.
解 由于
故
即
故由夹逼原理知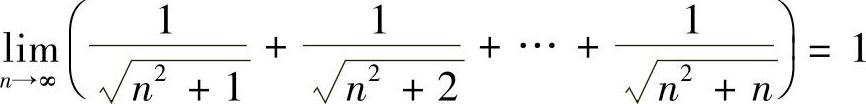 .
.
10.求极限 .
.
解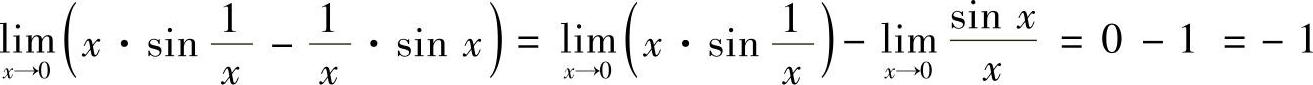
11.求极限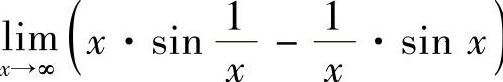 ).
).
解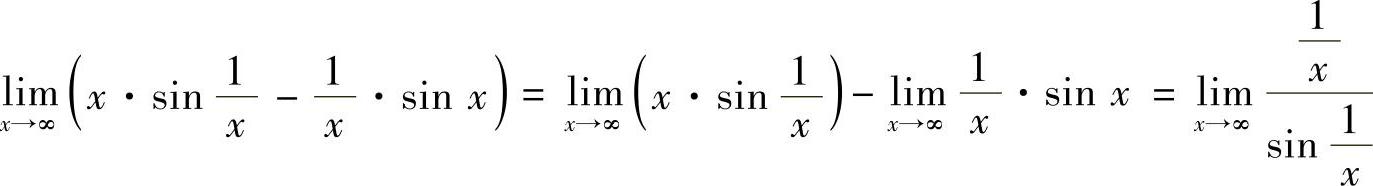 -0=1
-0=1
12.求极限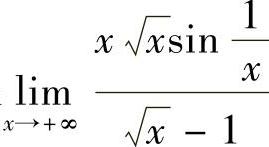 .
.
解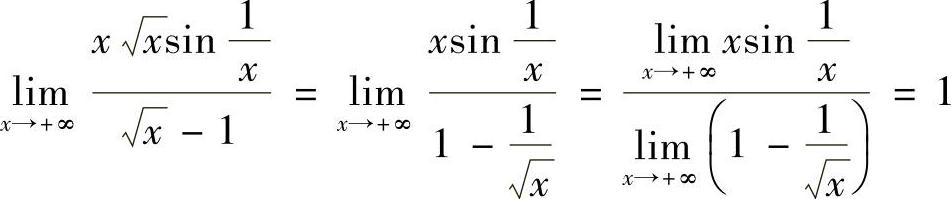
13.极限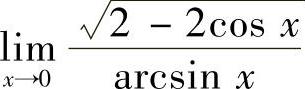 存在吗?
存在吗?
解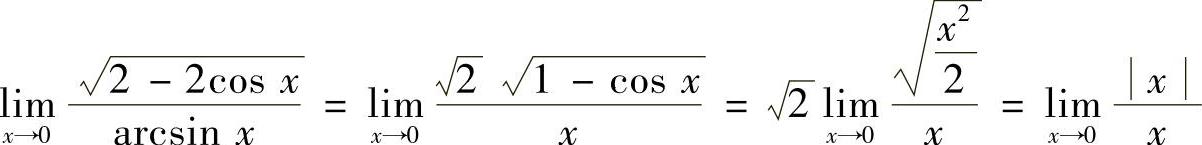 由于
由于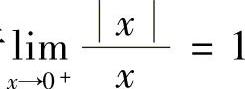 ,
,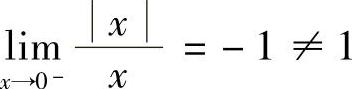 ,故
,故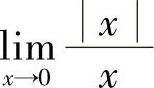 不存在,因此极限
不存在,因此极限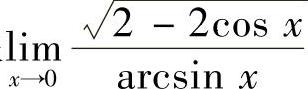 不存在.
不存在.
14.设×1>0,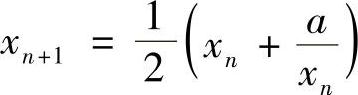 ,N=1,2,…,A>0,证:
,N=1,2,…,A>0,证: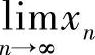 存在并求值.
存在并求值.
证 显然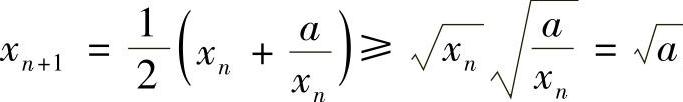 ,N=1,2,…,即×2N+1≥A,N=1,2,…,从而
,N=1,2,…,即×2N+1≥A,N=1,2,…,从而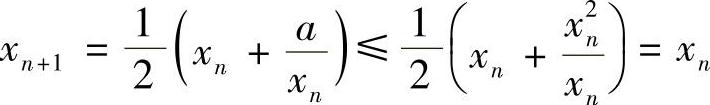 ,N=2,3,…,因此数列{×N}是单调递减有下界0的数列,故
,N=2,3,…,因此数列{×N}是单调递减有下界0的数列,故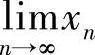 存在.
存在.
不妨设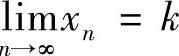 ,则由关系式
,则由关系式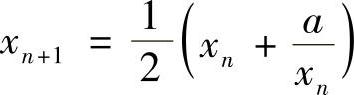 ,得
,得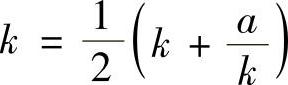 ,从而得到
,从而得到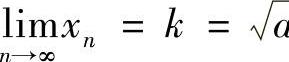 A.
A.
15.求极限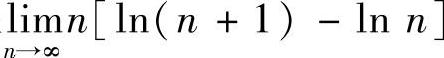 .
.
解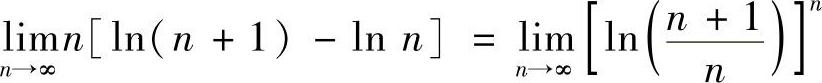
16.求极限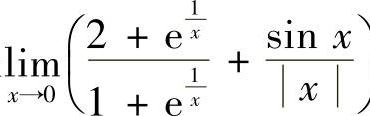 .
.
解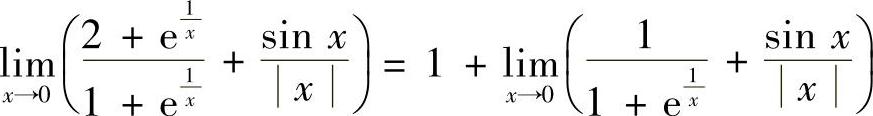 ,又因为
,又因为
故
因此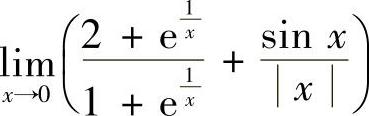 不存在.
不存在.
17.求极限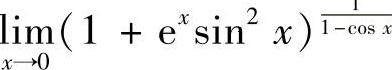 .
.
解 令u(×)=1+e× SIN2×,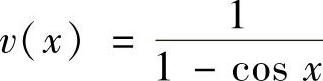 ,则
,则
因此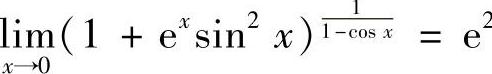 .
.
18.证明: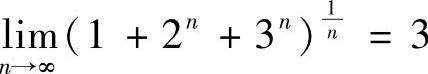 .
.
证 由于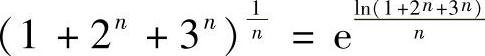 ,故
,故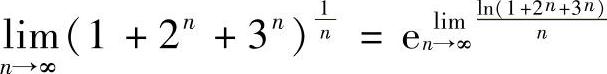 .又由于
.又由于
故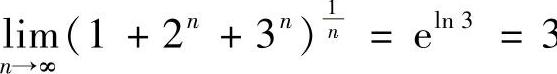 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








