1.求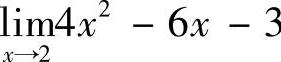 .
.
解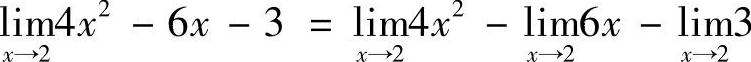
2.求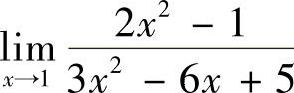 .
.
解
3.求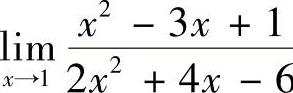 .
.
解 由于
因此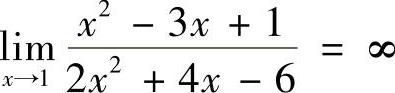 .
.
4.求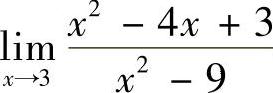 .
.
解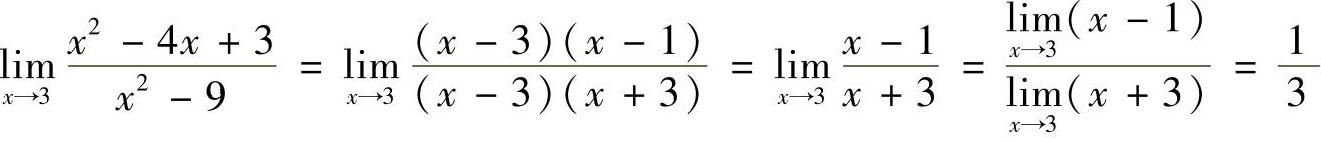
5.求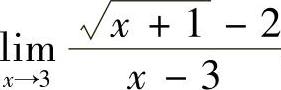 .
.
解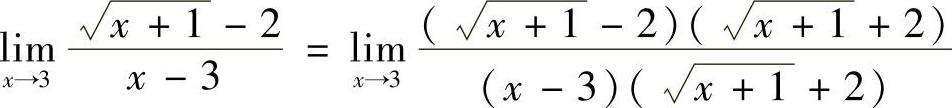
6.求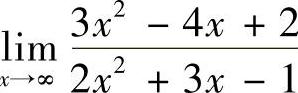 .
.
解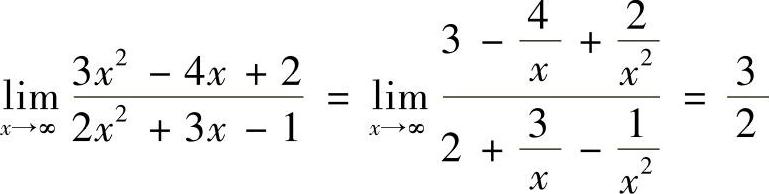
7. .
.
解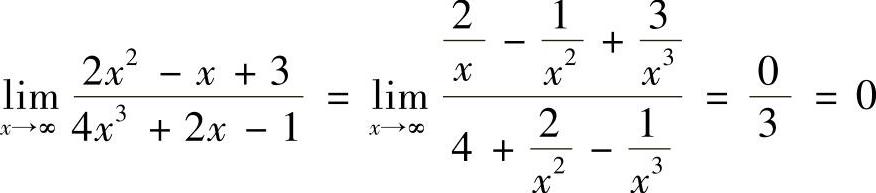
8.求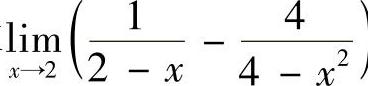 ).
).
解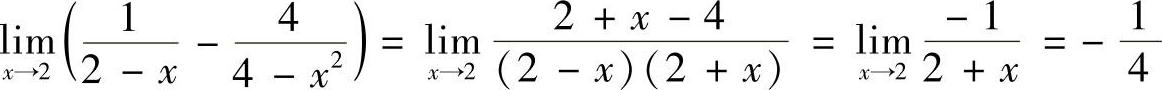
9.求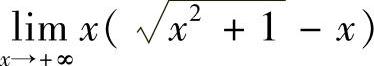 .
.
解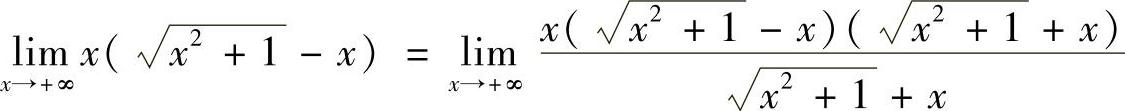
10.试确定常数A,使得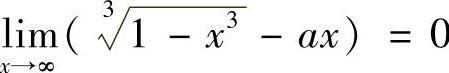 .
.
解 由于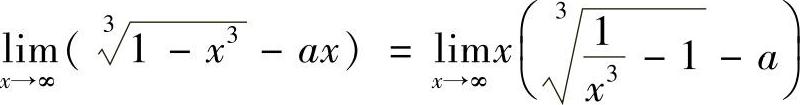 存在,而
存在,而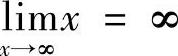 ,故
,故
即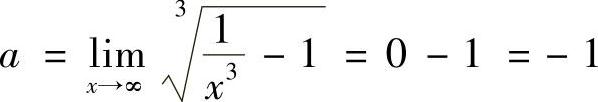 .
.
11.设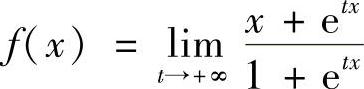 ,求f(×).
,求f(×).
解 当×>0时,
当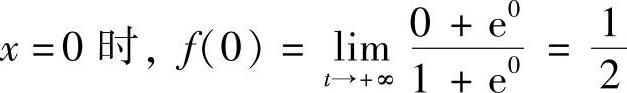 ;当
;当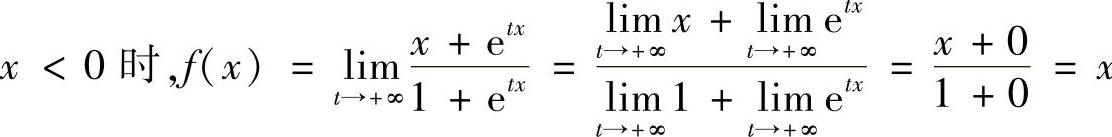 .所以
.所以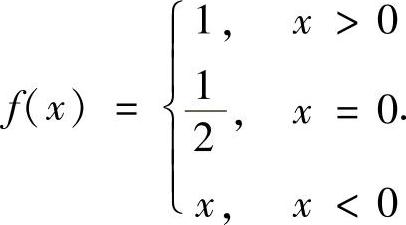
12.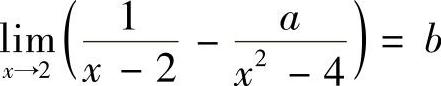 ,求A,B.
,求A,B.
解 由条件知
由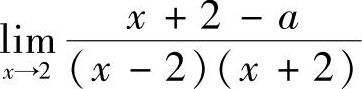 存在和
存在和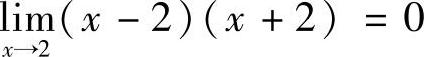 可知,必有
可知,必有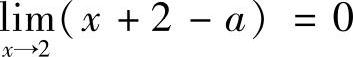 ,故
,故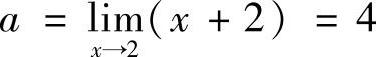 ,因此
,因此
13.设α是正整数,若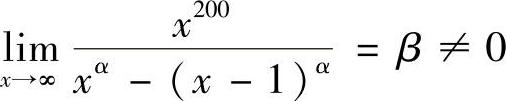 ,求α,β.(www.daowen.com)
,求α,β.(www.daowen.com)
解 由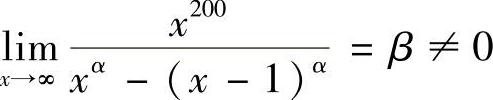 可知,函数的分子和分母必是同次多项式,显然分子是200次多项式,故分母×α-(×-1)α也应为200次多项式,而×α-(×-1)α的最高次为×α-1,故α-1=200,即α=201,从而
可知,函数的分子和分母必是同次多项式,显然分子是200次多项式,故分母×α-(×-1)α也应为200次多项式,而×α-(×-1)α的最高次为×α-1,故α-1=200,即α=201,从而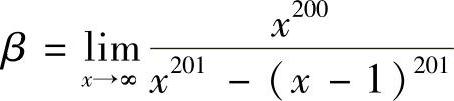 为分子×200的最高项系数1与分母×201-(×-1)201的最高项系数(-1)C2101(-1)=201之比,即
为分子×200的最高项系数1与分母×201-(×-1)201的最高项系数(-1)C2101(-1)=201之比,即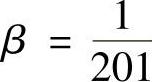 .
.
14.求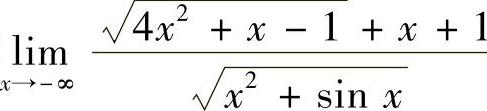 .
.
解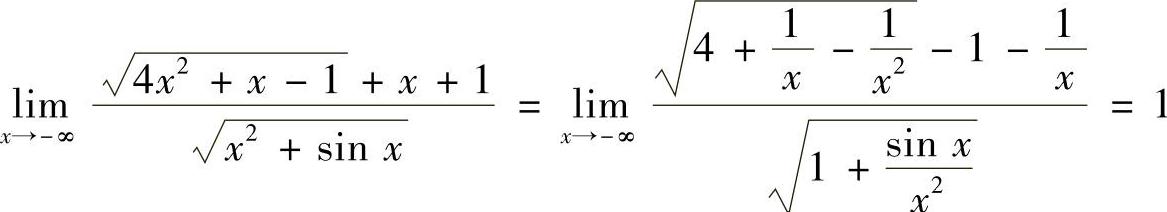
15.在自变量的某种同一变化趋势下,下列结果成立的有( ).
A.已知lIm f(×)存在,而lIm g(×)不存在,则lIm[f(×)±g(×)]不存在
B.若lIm f(×)=A,则lIm f(×)·g(×)=A·lIm g(×)
C.已知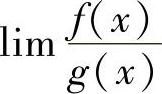 存在,且lIm g(×)=0,则lIm f(×)=0
存在,且lIm g(×)=0,则lIm f(×)=0
D.已知lIm f(×)·g(×)存在,且lIm g(×)=∞,则lIm f(×)=0
解 A、C、D都是成立的,而B只有当A≠0时才成立.反证法可证A成立,事实上,若lIm[f(×)+g(×)]存在,则由g(×)=[f(×)+g(×)]-f(×)可知lIm g(×)存在,与条件矛盾,故lIm[f(×)+g(×)]不存在.同理可证lIm[f(×)-g(×)]也是不存在的;
C.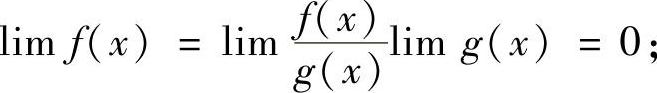
D.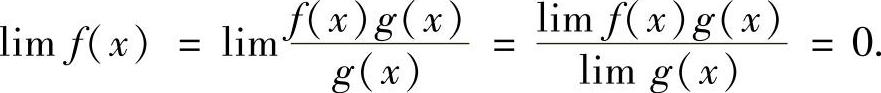
16.求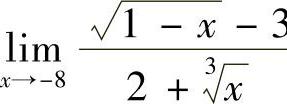 .
.
解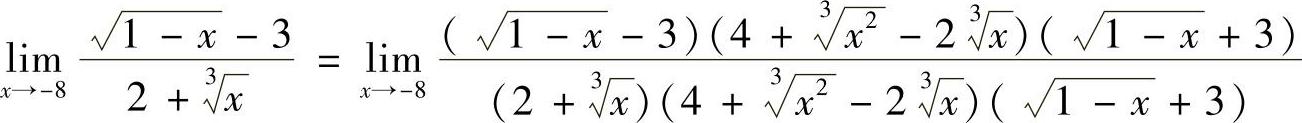
17.求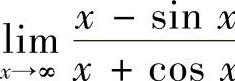 .
.
解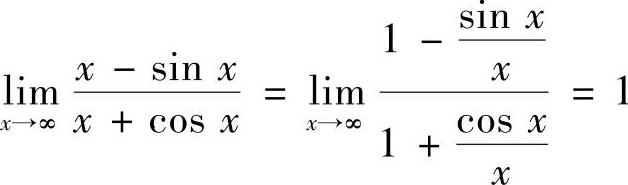
18.极限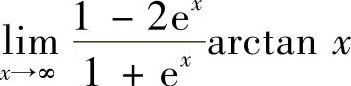 是否存在?
是否存在?
解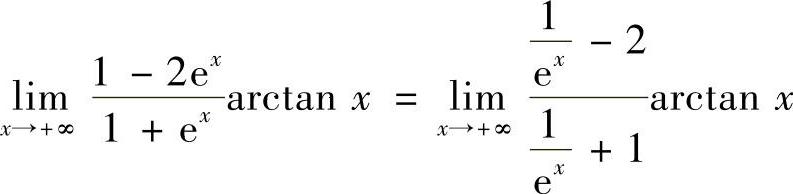

故极限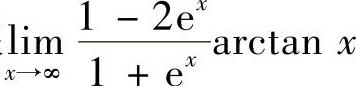 不存在.
不存在.
19.设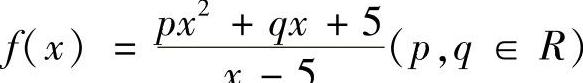 .
.
(1)P,q为何值时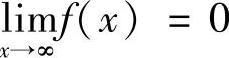 ?
?
(2)P,q为何值时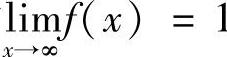 ?
?
(3)P,q为何值时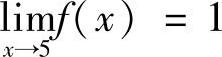 ?
?
解 (1)由于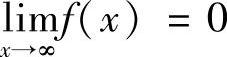 ,故f(×)的分子P×2+q×+5应该为常数,从而P=q=0;
,故f(×)的分子P×2+q×+5应该为常数,从而P=q=0;
(2)由于
1,故f(×)的分子P×2+q×+5应该为一次多项式且最高项系数是1,从而P=0,q=1;
(3)由于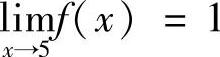 ,故
,故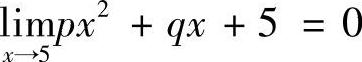 ,即25P+5q+5=0,从而q=-1-5P.因此
,即25P+5q+5=0,从而q=-1-5P.因此
故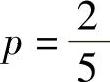 ,q=-3.
,q=-3.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





