1.观察下列数列变化趋势，写出它们的极限.

（1） （2）

解 （1）因为数列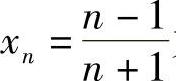为0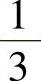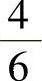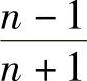，，，，，，…，，…，故数列的极限为1；

（2）因为数列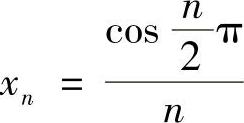为0，-，0，，0，-，0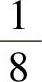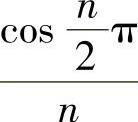，，…，，…，故数列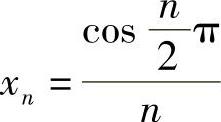的极限为0.

2.根据数列极限定义证明：.

证 由于N，故对∀ε＞0，可取N，则当N＞N有不等式×_N-A＜ε成立，所以.

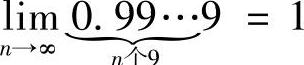3.已知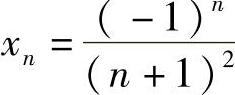，证明：数列｛×_N｝的极限为0.

证 由于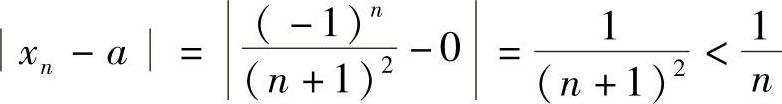，故对∀ε＞0，可取N＝，当N＞N有不等式×_N-A＜ε成立，所以0.

4.设数列｛×_N｝有界，又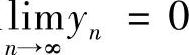，证明：（N+1）＝0.

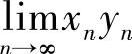证 不妨设数列｛×_N｝有界m，由，知对∀ε＞0，存在N，当N＞N时有ｙ_N^-0＜ε，从而有×_Nｙ_N-0≤mｙ_N＜mε，故＝0.

5.设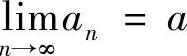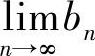，＝B.证明：若A＞B，则∃N，使得∀N＞N，有A_N＞B_N.

证 由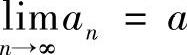可知，对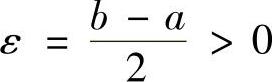，存在N₁，当N＞N₁有不等式A_N-A＜ε成立，从而有A-ε＜A_N.同理对上述的ε，存在N₂，当N＞N₂有不等式B_N-B＜ε成立，从而有B_N＜B+ε. 令N＝mA×｛N₁，N₂｝，则当N＞N时必有A-ε＜A_N和B_N＜B+ε同时成立，因此B_N＜B+ε＝A-ε＜A_N，即有A_N＞B_N.

6.若数列｛ｙ_N｝满足，N＝1，2，3，…，则当N→∞时，必有（）.

A.ｙ_N是无穷小量 B.ｙ_N是无界变量

C.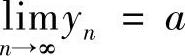 D.ｙ_N是无穷大量

解 正确答案是C.因为对∀ε＞0，可取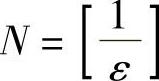，当N＞N有不等式成立，所以＝A.(www.daowen.com)

7.求极限.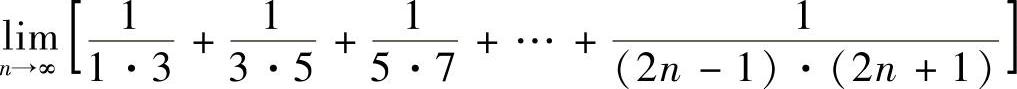

解]

8.若，求k的取值范围.

解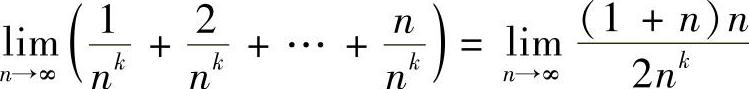，故当k＝2时，则；当k＞2时，则0＝0；当k＜2时，则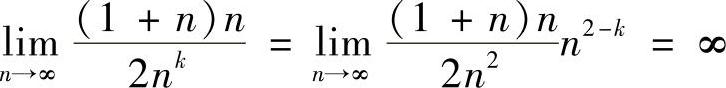.故若，必有k＞2.

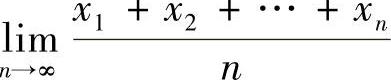9.若，证明：＝A.

证 由可知，即对∀ε＞0，存在正整数m，则当N＞m时有不等式×N-A＜ε成立.将m固定，有

即存在正整数N，当N＞N时，有ε.于是，对∀ε＞0，存在正整数N，当N＞N时有

即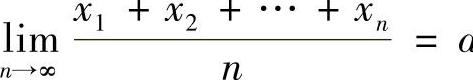A.

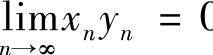10.设数列｛×_N｝有界，又，证明：0.

证 不妨设数列｛×_N｝有界m，由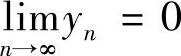，知对∀ε＞0，存在N，当N＞N时有ｙ_N-0＜ε，从而有×_Nｙ_N-0≤mｙ_N＜mε，故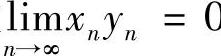0.

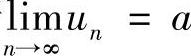11.若，证明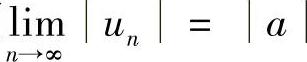.并举例说明数列｛ｕ_N｝有极限，但数列｛ｕ_N｝未必有极限.

证 由，知对∀ε＞0，存在N，当N＞N时有ｕ_N-A＜ε，从而有ｕ_N^-A≤ｕ_N-A＜ε，故.

举例：数列ｕ_N＝1，-1，1，-1，1…，则数列｛ｕ_N｝为常数列，故有极限1，但数列｛ｕ_N｝无极限.

12.对于数列｛×_N｝，证明：A.

证 由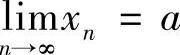，知对∀ε＞0，存在N＞1，当N＞N时有×_N-A＜ε，此时2N-1＞N＞N，从而有×_2N-1-A＜ε，故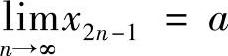.同理可证.反之，由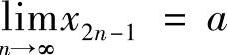知对∀ε＞0，存在N₁，当N＞N时有×_2N-1-A＜ε.由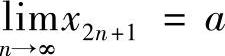知对上述的ε＞0，存在N₂，当N＞N时有×_2N+1-A＜ε.从而对上述的ε＞0，存在N＝mA×｛N₁，N₂｝，当N＞N时有×_2N-1-A＜ε和×_2N+1-A＜ε同时成立，即当N＞2N+1时，有×_N-A＜ε，故_NｌIm.