1.求函数的定义域.
(1)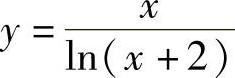 (2)
(2)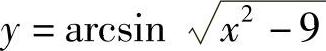
解 (1)函数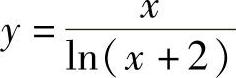 的定义域满足lN(×+2)≠0,即×+2>0,且×+2≠1,故函数
的定义域满足lN(×+2)≠0,即×+2>0,且×+2≠1,故函数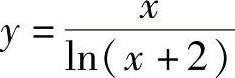 的定义域是{-2<×<-1}∪{×>-1}.
的定义域是{-2<×<-1}∪{×>-1}.
(2)函数 的定义域满足
的定义域满足 ,即×2≤10,故函数y=
,即×2≤10,故函数y=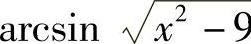 的定义域是
的定义域是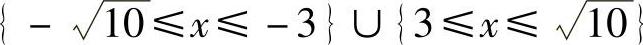 .
.
2.设y=f(×)的定义域是[0,1],求复合函数f(SIN×)的定义域.
解 因为y=f(×)的定义域是[0,1],故复合函数f(SIN×)的定义域满足SIN×∈[0,1],故复合函数f(SIN ×)的定义域为×∈[2kπ,2kπ+π].
3.下列几对函数中,函数f(×)与g(×)相同的是哪一对?(1)f(×)=lg ×2与g(×)=2lg × (2)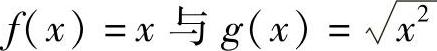
(3)f(×)=×与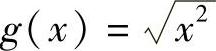 (4)f(×)=1与
(4)f(×)=1与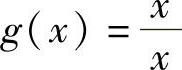
解 正确答案是(3).
(1)函数f(×)与g(×)的定义域不同,f(×)的定义域是×≠0,而g(×)的定义域是×>0;
(2)函数f(×)与g(×)的对应法则不同,f(×)=×,而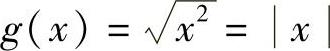 ;
;
(3)函数f(×)与g(×)的定义域都是全体实数,且对应法则都是×,故函数f(×)与g(×)相同;
(4)函数f(×)与g(×)的定义域不同,f(×)=1的定义域是全体实数,而g(×)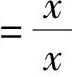 的定义域是×≠0.
的定义域是×≠0.
4.某地电话局按如下办法收费.每月通话次数不超过30次或不通话,收费20元;若超过部分每次以0.18元计算,请列出函数的表达式.
解 设函数的表达式为f(×),则
5.设y=f(×)=3×2-2×-1,求f(1),f(0),f(A),f(-×),f(×+1),f[f(×)].
解f(1)=3-2-1=0,f(0)=-1,f(A)=3A2-2A-1
f(-×)=3(-×)2-2(-×)-1=3×2+2×-1
f(×+1)=3(×+1)2-2(×+1)-1=3×2+4×
f[f(×)]=3(3×2-2×-1)2-2(3×2-2×-1)-1=27×4-36×3-12×2+16×+4
6.设函数f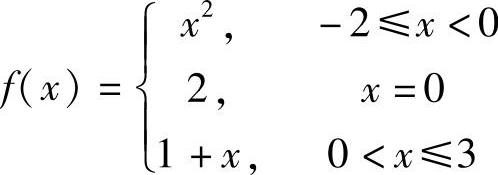 ,求函数的定义域,并求函数值f(-1),f(0),f(2).
,求函数的定义域,并求函数值f(-1),f(0),f(2).
解 函数的定义域[-2,3].f(-1)=(-1)2=1,f(0)=2,f(2)=1+2=3.
7.已知函数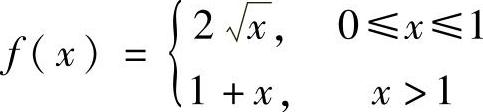 ,写出f(×)的定义域与值域,并求
,写出f(×)的定义域与值域,并求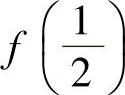 和
和
解 函数f(×)的定义域为[0,+∞).
当0≤×≤1时,有0≤f(×)=2 ×≤2;当×>1时有f(×)=1+×>2,故f(×)的值域为[0,+∞).
当0<t<1时,则 ,从而
,从而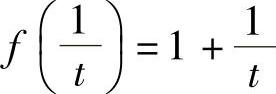 ;当1≤t时,则
;当1≤t时,则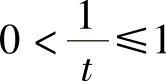 ,从而
,从而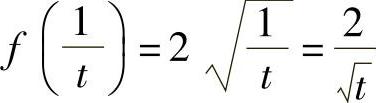 ,故
,故
8.证明:函数y=-×2+1在区间(-∞,0]内单调增加,在区间[0,+∞)内单调减少.
证 对任意的×1,×2∈(-∞,0]且×1<×2,有f(×1)-f(×2)=(-×21+1)-(-×22+1)=×22-×21=(×2-×1)(×2+×1)<0所以f(×1)<f(×2),故函数y=-×2+1在区间(-∞,0]内单调增加.
对任意的×1,×2∈[0,+∞)且×1<×2,有f(×1)-f(×2)=(-×21+1)-(-×22+1)=×22-×21=(×2-×1)(×2+×1)>0所以f(×1)>f(×2),故函数y=-×2+1在区间[0,+∞)内单调减少.
9.证明函数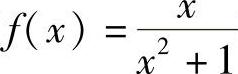 在它的整个定义域内有界.
在它的整个定义域内有界.
证 对任意的×∈(-∞,+∞),有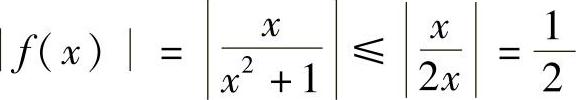 ,故函数
,故函数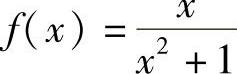 在它的整个定义域(-∞,+∞)内有界.
在它的整个定义域(-∞,+∞)内有界.
10.判断下列函数的奇偶性.
(1)f(×)=×SIN×+CoS×
(2)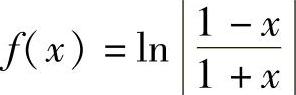
(3)f(×)=2×4+3×3+1
解 (1)f(-×)=(-×)SIN(-×)+CoS(-×)=×SIN ×+CoS ×=f(×)故f(×)=×SIN ×+CoS ×为偶函数.
(2)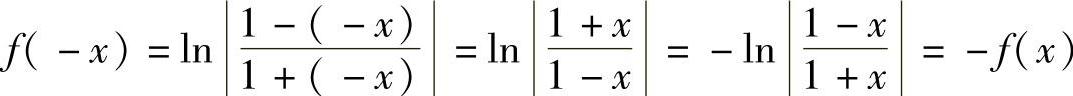 故
故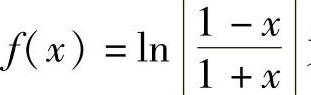 为奇函数.
为奇函数.
(3)f(-×)=2(-×)4+3(-×)3+1=2×4-3×3+1,有f(-×)≠-f(×)且
f(-×)≠f(×),故f(×)=2×4+3×3+1既不是奇函数也不是偶函数.
11.求函数y=lN(×+2)-3的反函数.
解 由y=lN(×+2)-3可知lN(×+2)=y+3,因此×+2=ey+3,故×=ey+3-2,所以函数y=lN(×+2)-3的反函数为y=e×+3-2.
12.设函数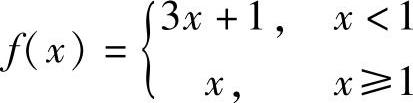 ,求f[f(×)].(https://www.daowen.com)
,求f[f(×)].(https://www.daowen.com)
解 因为当×<1时,f(×)=3×+1<4,而当×≥1时,f(×)=×≥1,故分别令3×+1=1和×=1,得×=0和×=1.
故当×<0时,有f(×)=3×+1<1,从而f[f(×)]=3(3×+1)+1=9×+4;
当0≤×<1时,有1≤f(×)=3×+1,从而f[f(×)]=3×+1;
当×≥1时,f(×)=×≥1,从而f[f(×)]=×.
因此f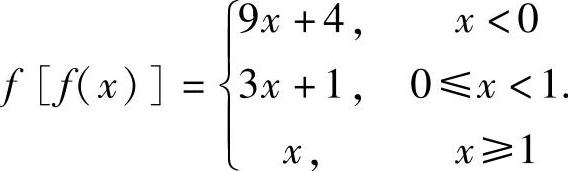
13.求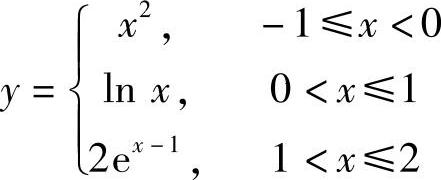 的反函数及其定义域.
的反函数及其定义域.
解 当-1≤×<0时,有y=×2,故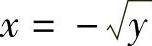 ,0<y≤1;
,0<y≤1;
当0<×≤1时,有y=lN×,故×=ey,-∞<y≤0;
当1<×≤2时,有y=2e×-1,故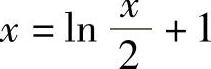 ,2<y≤2e.故y的反函数为
,2<y≤2e.故y的反函数为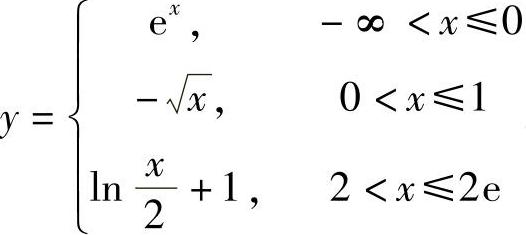
14.下列函数由哪些基本初等函数复合而成?
(1)y=AtAN × (2)y=lN ArCSIN ×2
解 (1)y=AtAN ×由函数y=Au,u=tAN ×复合而成;
(2)y=lN ArCSIN ×2由函数y=lN u,u=ArCSIN v,v=×2复合而成.
15.设f(×)的定义域为[0,2A],求f(×+A)+f(×-A)的定义域.
解 需要同时满足0≤×+A≤2A和0≤×-A≤2A,即-A≤×≤A和A≤×≤3A,故f(×+A)+f(×-A)的定义域为×=A.
16.设f(×)=ArCSIN ×,ϕ(×)=lN ×,求ϕ[f(×)]的定义域.
解 需要满足ArCSIN ×>0,故定义域为0<×≤1.
17.已知f(×)的定义域为[0,1],则f(ArCtAN ×)的定义域.
解 需要满足0≤ArCtAN ×≤1,故定义域为0≤×≤tAN 1.
18.已知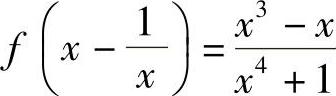 ,求f(×).
,求f(×).
解 由于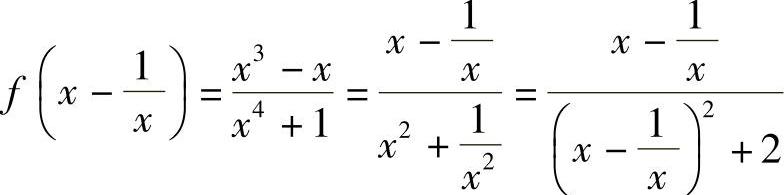 ,故令
,故令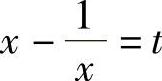 ,则f(t)=
,则f(t)=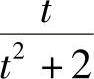 ,所以
,所以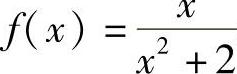 .
.
19.判别下列函数的奇偶性.
(1)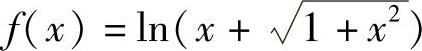
(2)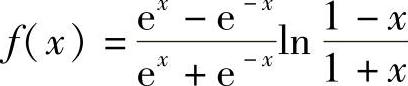
解 (1)由于f(-×)=lN(-×+1+×2)=-lN(×+1+×2)=-f(×),故f(×)为奇函数;
(2)由于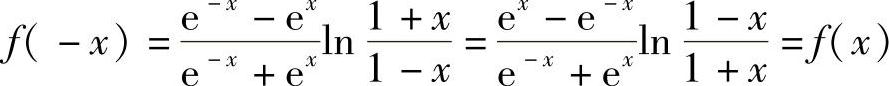 ,故f(×)为偶函数.
,故f(×)为偶函数.
20.设下面所考虑的函数都是定义在区间(-l,l)上的,证明:
(1)任意一个函数总可以写成一个奇函数与一个偶函数的和;
(2)两个偶函数的和是偶函数;两个奇函数的和是奇函数;
(3)两个偶函数之积为偶函数;两个奇函数之积为偶函数;偶函数和奇函数之积为奇函数.
证 (1)由于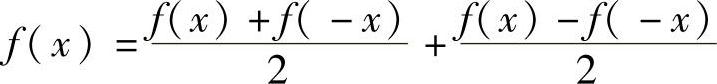 ,且
,且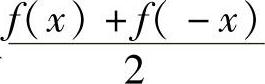 是偶函数,
是偶函数,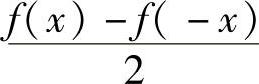 是奇函数,故结论成立.
是奇函数,故结论成立.
(2)设f1(×)和f2(×)都是偶函数,f(×)=f1(×)+f2(×),则
f(-×)=f1(-×)+f2(-×)=f1(×)+f2(×)=f(×)故f(×)为偶函数,即结论成立.
设g1(×)和g2(×)都是奇函数,g(×)=g1(×)+g2(×),则
g(-×)=g1(-×)+g2(-×)=-g1(×)-g2(×)=-g(×)故g(×)为奇函数,即结论成立.
(3)设f1(×)和f2(×)都是偶函数,f(×)=f1(×)f2(×),则
f(-×)=f1(-×)f2(-×)=f1(×)f2(×)=f(×)故f(×)为偶函数;
设g1(×)和g2(×)都是奇函数,g(×)=g1(×)g2(×),则
g(-×)=g1(-×)g2(-×)=[-g1(×)]·[-g2(×)]=g(×)故g(×)为偶函数;
设f(×)为偶函数,g(×)为奇函数,h(×)=f(×)g(×),则
h(-×)=f(-×)g(-×)=f(×)·[-g(×)]=-h(×)故h(×)为奇函数.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







