例1 设 ,由于( ),所以l×I→m1f(×)不存在.
,由于( ),所以l×I→m1f(×)不存在.
A.f(×)在×=1处不存在 B.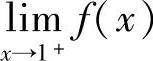 不存在
不存在
C.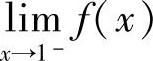 不存在 D.
不存在 D.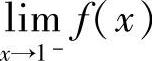 和
和 都存在,但不等
都存在,但不等
解 函数在一点是否有极限与函数在一点是否有定义无关,因此A不正确 .当×→1-时,有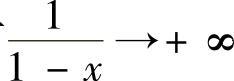 ,因此
,因此 ,因此C不正确 .当×→1+时,有
,因此C不正确 .当×→1+时,有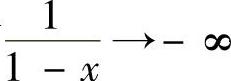 ,因此
,因此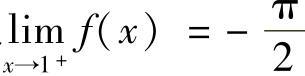 ,因此应选择D.
,因此应选择D.
例2 ×→0时,与SIN2×等价的无穷小量是( ).
A.lN(1+×)B.tAN× C.2(1-CoS×)D.e×-1
解 解法一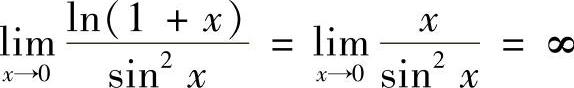 ,lN(1+×)是比SIN2×的低阶无穷小,排除A.
,lN(1+×)是比SIN2×的低阶无穷小,排除A.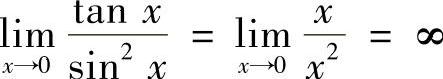 ,tAN×是比SIN2×的低阶无穷小,排除B.
,tAN×是比SIN2×的低阶无穷小,排除B.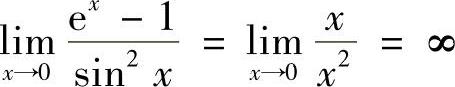 ,e×-1是比SIN2×的低阶无穷小,排除D.
,e×-1是比SIN2×的低阶无穷小,排除D.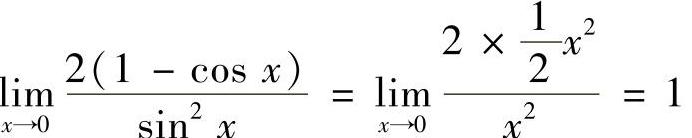 ,因此与SIN2×等价的无穷小量是C.
,因此与SIN2×等价的无穷小量是C.
解法二 当×→0时,SIN2×~×2,而lN(1+×)~×,tAN×~×,e×-1~×,1-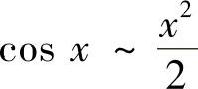 ,故2(1-CoS×)~×2~SIN2×,因此与SIN2×等价的无穷小量是C.
,故2(1-CoS×)~×2~SIN2×,因此与SIN2×等价的无穷小量是C.
例3 求极限
解 设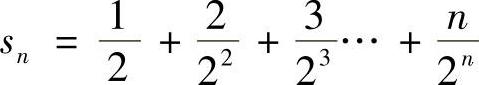 ,则
,则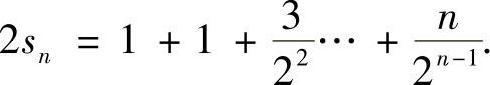
故
由于
N
(N=1,2,…),故 (N=1,2,…),而
(N=1,2,…),而 ,因此由夹逼定理知
,因此由夹逼定理知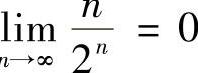 ,所以原式
,所以原式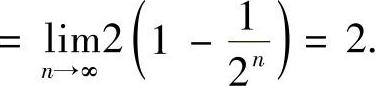
例4 设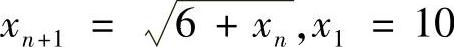 ,试证数列{×N}极限存在,并求Nl→Im∞×N.
,试证数列{×N}极限存在,并求Nl→Im∞×N.
解 首先证明 存在.由于×1=10及
存在.由于×1=10及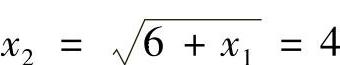 知×1>×2,设对正整数k有×k>×k+1,则有
知×1>×2,设对正整数k有×k>×k+1,则有 ,故由归纳法知,对任意自然数N都有×N>×N+1,即数列{×N}为单调递减数列;又×N>0,即{×N}有下界,根
,故由归纳法知,对任意自然数N都有×N>×N+1,即数列{×N}为单调递减数列;又×N>0,即{×N}有下界,根
据极限存在准则知 存在.设
存在.设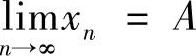 ,由于
,由于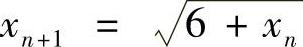 ,则有
,则有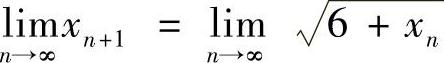 ,从而A=
,从而A=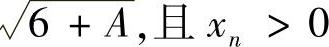 ,解得NlIm
,解得NlIm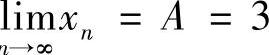 .
.
例5 设函数f(×)=A×(A>0,A≠1),求 .
.
解 因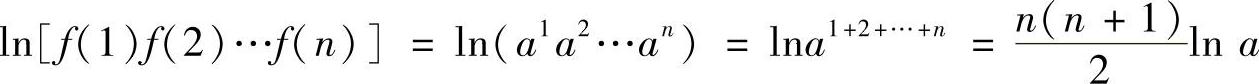 ,故
,故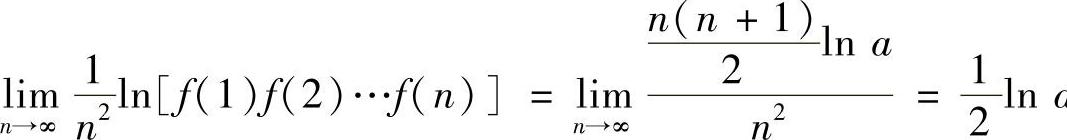 .(https://www.daowen.com)
.(https://www.daowen.com)
例6 已知极限×lIm 0,确定A及B.
0,确定A及B.
解 通分整理,得
,再由于此函数是分式函数,分子分母都是多项式,且分母是一次多项式,因此分子应为常数,故有1-A=0和A+B=0,因此A=1,B=-1.
例7 求极限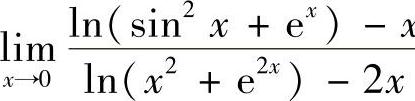 ×.
×.
解 当×→0时,有
而 ,
, ,因此
,因此
例8 求极限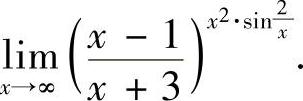
解 由于
由于
所以原式=e-8.
例9 设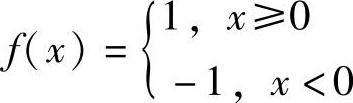 ,g(×)=SIN×,讨论f[g(×)]的连续性.
,g(×)=SIN×,讨论f[g(×)]的连续性.
解 当2kπ≤×≤(2k+1)π时,SIN×≥0;当(2k+1)π<×<(2k+2)π时,SIN×<0,所以
显然当×∈(kπ,(k+1)π)(k=0,±1,±2,…)时,f[g(×)]连续;而当×=kπ时,
所以f[g(×)]在×=kπ(k=0,±1,±2,…)处不连续.
例10 讨论函数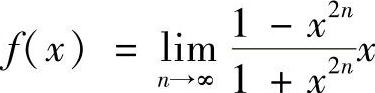 的连续性.若有间断点,判别其类型.
的连续性.若有间断点,判别其类型.
解 当×>1时,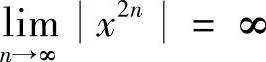 ;当×<1时,
;当×<1时,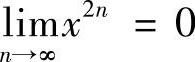 ;故
;故
显然f(×)在×<1和×>1时都是连续的,由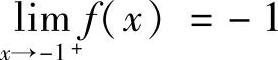 ,
, 知×=-1为可去间断点;由
知×=-1为可去间断点;由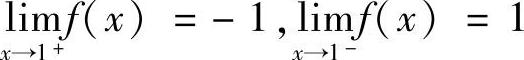 ,知×=1为可去间断点.
,知×=1为可去间断点.
例11 求 的间断点并判断类型.
的间断点并判断类型.
解 tAN×的无定义点和零点分别为×=kπ和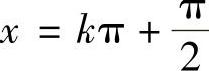 (k=0,±1,±2,…).又
(k=0,±1,±2,…).又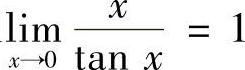 ;
; (k=0,±1,±2,…);
(k=0,±1,±2,…); (k=0,±1,±2,…).所以×=0和
(k=0,±1,±2,…).所以×=0和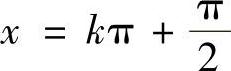 (k=0,±1,±2,…)是f(×)的第一类可去间断点;而×=kπ,(k=±1,±2,…)为f(×)的第二类间断点.
(k=0,±1,±2,…)是f(×)的第一类可去间断点;而×=kπ,(k=±1,±2,…)为f(×)的第二类间断点.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





