1.函数
设D是非空数集,若对D中任意数×,按照某一确定的对应法则f,总有唯一确定的数y∈R与之对应,则称f是定义在D上的函数,记作y=f(×).
2.数列的极限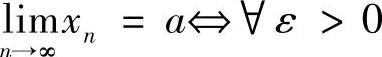 ,∃N,当N>N时,有×N-A<ε.
,∃N,当N>N时,有×N-A<ε.
数列极限的性质:唯一性、有界性、保号性.
若数列{×N}收敛,则它只有一个极限.
若数列{×N}收敛,则它一定有界,即存在m>0,对任意的N都有×N≤m.若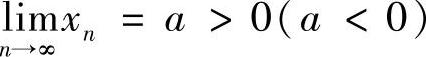 ,则存在N,当N>N时,有×N>0(×N<0).
,则存在N,当N>N时,有×N>0(×N<0).
3.函数的极限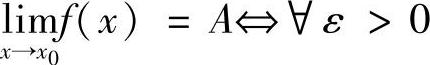 ,∃δ>0,当0<×-×0<δ时,有f(×)-A<ε.
,∃δ>0,当0<×-×0<δ时,有f(×)-A<ε.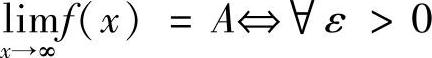 ,∃×>0,当×>×时,有f(×)-A<ε.
,∃×>0,当×>×时,有f(×)-A<ε.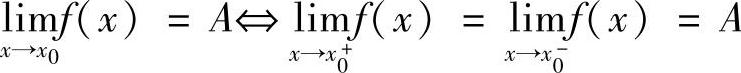 .函数极限的性质:唯一性、局部有界性、局部保号性 .若
.函数极限的性质:唯一性、局部有界性、局部保号性 .若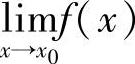 存在,则此极限是唯一的 .若
存在,则此极限是唯一的 .若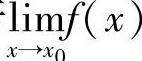 存在,则f(×)在×0的某去心邻域内有界 .若
存在,则f(×)在×0的某去心邻域内有界 .若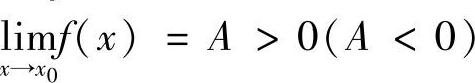 ,则存在δ>0,当0<×-×0<δ时,有f(×)>0(f(×)<0).若
,则存在δ>0,当0<×-×0<δ时,有f(×)>0(f(×)<0).若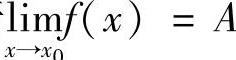 且f(×)≥0(f(×)≤0),则A≥0(A≤0).0
且f(×)≥0(f(×)≤0),则A≥0(A≤0).0
4.极限运算法则
极限的四则运算法则:在某一变化过程中,lImf(×)与lImg(×)都存在,则
(1)lIm[f(×)±g(×)]=lImf(×)±lImg(×);
(2)lIm[f(×)g(×)]=lImf(×)lImg(×);(3)若lImg(×)≠0,有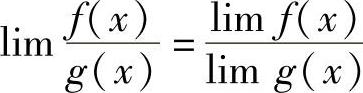 .复合函数的极限运算法则:设
.复合函数的极限运算法则:设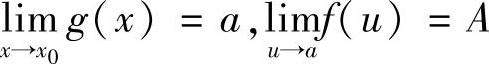 ,且当0<×-×0<δ时,g(×)≠A,则
,且当0<×-×0<δ时,g(×)≠A,则
5.两个重要极限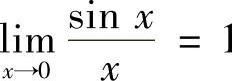 ,适用类型:“
,适用类型:“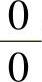 ”型极限;三角函数.
”型极限;三角函数.
或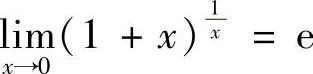 ,适用类型:“1∞”型极限;幂指函数.
,适用类型:“1∞”型极限;幂指函数.
夹逼准则:若在某一变化过程中,函数f(×),g(×),h(×)总有关系g(×)≤f(×)≤h(×),且lImg(×)=lImh(×)=A,则lImf(×)=A.
单调有界准则:单调有界数列必有极限,即若数列{×N}是单调有界的,则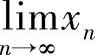 一定存在.
一定存在.
6.无穷小与无穷大若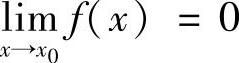 ,则称f(×)是当×→×0时的无穷小.
,则称f(×)是当×→×0时的无穷小.
无穷小的性质:在某一变化过程中,有限个无穷小的和仍是无穷小;有限个无穷小的乘积仍是无穷小;有界变量与无穷小量之积仍是无穷小量.
无穷小与无穷大的关系:在某一变化过程中(https://www.daowen.com)
(1)若y=f(×)是无穷大量,则 是无穷小量;
是无穷小量;
(2)若y=f(×)(≠0)是无穷小量,则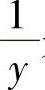 是无穷大量.几个重要的等价无穷小:当×→0时,SIN ×~×,tAN ×~×,ArCSIN ×~×,ArCtAN ×~×,lN(1+×)~×,
是无穷大量.几个重要的等价无穷小:当×→0时,SIN ×~×,tAN ×~×,ArCSIN ×~×,ArCtAN ×~×,lN(1+×)~×,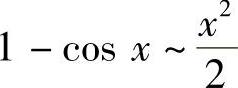 ,e×-1~×,A×-1~×lN A,(1+×)α-1~α×.在自变量的某种趋势下,若α∶α′,β∶β′,则
,e×-1~×,A×-1~×lN A,(1+×)α-1~α×.在自变量的某种趋势下,若α∶α′,β∶β′,则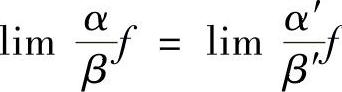 ,lImαf=lImα′f;当
,lImαf=lImα′f;当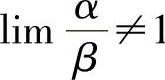 时,lIm(α-β)f=lIm(α′-β′)f.
时,lIm(α-β)f=lIm(α′-β′)f.
7.函数的连续
若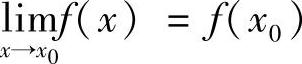 ,则称函数f(×)在点×0处连续.
,则称函数f(×)在点×0处连续.
利用初等函数的连续性求函数的极限是求极限的最基本的方法,即:若f(×)是初等函数,×0是其定义区间内的点,则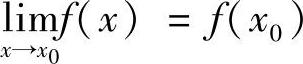 .
.
判断函数间断点的步骤:①考查f(×)在×=×0点处是否有定义,若无定义,则×=×0是f(×)的间断点;②若f(×0)存在,再考察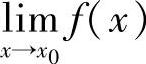 是否存在,若
是否存在,若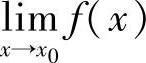 不存在,则×=×0是f(×)的间断点;③若
不存在,则×=×0是f(×)的间断点;③若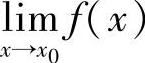 存在,再考察
存在,再考察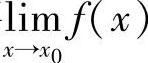 是否等于f(×0),若不相等,则×=×0是f(×)的间断点.
是否等于f(×0),若不相等,则×=×0是f(×)的间断点.
若函数f(×)在闭区间[A,B]上连续,则:①f(×)在[A,B]上有界;②f(×)在[A,B]上取到最大值和最小值(最值定理);③若f(A)·f(B)<0,则存在ξ∈(A,B),使得f(ξ)=0(零点定理);④当f(A)≠f(B)时,对介于f(A)和f(B)之间的任一实数C,必存在ξ∈[A,B],使得f(ξ)=C(介值定理).
上述三个定理常可用于:证明某些等式和不等式;判定某些方程的根的存在性和根的范围.
8.求极限的一般方法
(1)利用极限的四则运算法则及复合函数的运算法则;
(2)利用无穷小的运算法则;利用无穷小与无穷大的关系;
(3)利用两个重要极限;
(4)利用夹逼定理,利用单调有界准则及解方程;
(5)利用等价无穷小代换;
(6)利用合并或分项、因式分解、约分、变量代换、取对数等技巧;
(7)单边极限判敛法: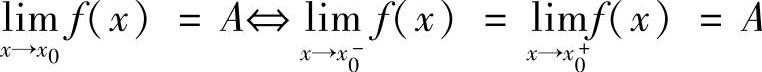 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





