正如无穷公理的丰富推论所揭示的，对实无穷的接纳让人类得以打开通向新世界的大门。第一个无穷集ω出现之初的确给习惯于生活在HF世界中的人们制造了一些慌乱。但人们很快发现，所谓伽利略悖论、斯寇伦悖论（见第125页）、巴拿赫-塔斯基悖论并不是什么悖论，而只是揭示了人们直观的模糊之处，并让概念世界更清晰地呈现在人们面前。哥德尔将这些现象与发生在天文学中的现象做对比：

存在这种情况，我们把两个或更多个明晰概念（sharp concept）混淆为一个直观概念（intuition concept），然后我们似乎得到了相悖的结果。……当我们意识到有两个不同的明晰概念被混淆为一个直观概念时，悖论就消失了。这里可以与感觉知觉类比。我们无法分辨远距离的两颗相邻的星球，但通过望远镜，我们能看到确实有两颗星球。（Wang，1996，p. 234）

大基数公理被认为是对无穷公理的推广。

定义　4.13（不可达基数）　称不可数基数κ是不可达基数（inaccessible cardinal），当且仅当κ满足以下两个条件：

（1）对任意基数λ＜κ，有2λ＜κ（κ是强极限基数）；

（2）对任意θ＜κ以及由＜κ的序数组成的非降序列〈αξ〉ξ＜θ，该序列的极限limξ＜θαξ＜κ。

也就是说，不可达基数被定义为无法从更小的基数通过取幂集的基数或取极限达到的不可数基数，而后两者是除了无穷公理以外ZFC公理赋予的仅有的两种获得更大基数的运算。事实上，无穷公理所断言存在的ω相对于比它小的基数（自然数）已经是不可达的了。正因为如此，Vω=HF成为（ZFC-无穷公理）的模型。类似地，如果κ是不可达基数，那么Vκ=H（κ）（遗传地＜κ的集合族，参见第145页对遗传有穷的定义），并且VκZFC。也因此，（ZFC+存在不可达基数）⊢Con（ZFC），大基数公理往往带来更高的证明论强度。

大基数公理是无穷公理的自然推广且带来更高的证明论强度，那么它们又是否能用来处理具体的描述集合论问题呢？索罗维的定理4.8提示，大基数公理的确可能有助于回答描述集合论的问题。梅切尔斯基的定理4.12则表示，即使希望通过决定性公理来证明可定义实数集的正则性质，也必须引入大基数。谢拉在（Shelah，1984）证明了：

定理　4.14　假设ZF+DC+所有集合都是勒贝格可测的，那么ω1在L中是不可达基数。因此，

Con（ZF+DC+所有集合都是勒贝格可测的）

→Con（ZFC+存在不可达基数）。

也就是说，索罗维在定理4.8中对不可达基数的使用是必要的。

据报道，索罗维在20世纪60年代就猜测大基数可以用来解决描述集合论问题。事实上，作为定理4.8的推论，索罗维在（Solovay，1969）证明了下述ZFC定理：

定理　4.15　假设存在一个可测基数，那么所有集合都具有完美集性质、贝尔性质并且是勒贝格可测的。

可测基数（measurable cardinal）概念早在1930年由乌拉姆（Ulam，Stanisław）提出（Ulam，1930）。一个不可数基数是可测基数，当且仅当存在一个关于κ子集的＜κ-可加的非平凡二值测度。所谓二值测度，就是判定任意κ的子集是“大”（非0测度）还是“小”（0测度）。如果一个测度只看κ的子集是否含有某个特定的元素，那么这个测度是平凡的。二值测度又可以用偏序（P（κ），⊂）上的（又称κ上的）超滤子（ultrafilter）来表示（参见定义3.17）。定义偏序（P（X），⊂）上的滤子U是一个超滤子，当且仅当对任意Y∈X，要么Y∈U，要么X \Y∈U。直观上，属于U的集合是“大”的，而补集“大”的集合是“小”的。超滤子将所有X子集划分为“大”的和“小”的。超滤子U是主超滤子（principal ultrafilter），当且仅当存在x∈X使得U={Y⊂X|x∈Y}。而我们称滤子U是κ-完全的，当且仅当任意＜κ个“大”的集合的交仍然是大的。由此，一个不可数基数是可测基数，当且仅当存在κ上的＜κ-完全非主超滤子。

容易证明，第一个无穷基数ω上就有一个有穷可加的非平凡的二值测度。^[15]但是ℵ1就不是可测基数。假设U是ω1上的可数完全非主超滤子。我们知道，连续统的基数2ℵ0≥ℵ1，也即可以用ℵ1枚举部分以ℵ0为定义域的二值函数〈fξ：ξ＜ω1〉。对任意n＜ω，要么{ξ＜ω1|fξ（n）=0}∈U，要么{ξ＜ω1|fξ（n）=1}∈U。令An是大的那个。由＜ℵ1-完全性，∩

n＜ωAn也是大的。但∩n＜ωAn同时是个单点集{f}，这与U是非主的矛盾。事实上，可以证明可测基数总是一个不可达基数。

斯科特（Scott，Dana Stewart）和基斯勒（Keisler，Howard Jerome）分别发表于（Scott，1961）和（Keisler，1962）的结果让可测基数有了另一个基于初等嵌入（elementrary embedding）的等价定义，标志着现代大基数理论的诞生。我们称单射e：M→N是从结构（M，∈）到（N，∈）的初等嵌入，当且仅当对任意集合论公式、任意∈M有

也就是说，e把M嵌入为N的一个初等子结构。

定理　4.16（基斯勒-斯科特）下列命题等价：

（1）κ是可测基数。

（2）存在传递类M和非平凡的初等嵌入j：V→M，使得κ是j的关键点（critical point）。

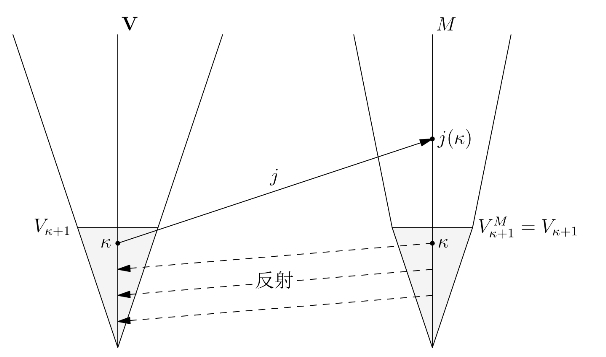
图4.3　非平凡初等嵌入

如果j：V→M是一个初等嵌入的话，那么M与V满足同样的命题，且对任意集合a，“V对a的看法”与“M对j（a）的看法”是一样的。特别地，j将V中的序数映射为M中的序数，并且是严格递增的。可以证明，非平凡的（非等同函数）初等嵌入总是会改变一个序数（即第一个被改变的集合在冯·诺伊曼层谱中所处的层数）。我们称第一个被改变的序数κ为初等嵌入j：V→M的关键点，又记作crit（j）=κ。显然，j（κ）＞κ。此外，由于对任意a∈Vκ有j（a）=a，因此=Vκ。而对任意X⊂Vκ有j（X）∩=X，因而=Vκ+1（见图4.3）。

反射论证

利用初等嵌入的等价定义容易证明：可测基数κ是一系列不可达基数的极限。已知κ本身是不可达基数，这是在Vκ+1中的局部性质。而=Vκ+1，因此，κ在M中也是不可达基数。在M看来，存在一个比j（κ）小的不可达基数。又由于j：V→M是初等嵌入，在V看来，就存在一个＜κ的不可达基数。而对任意＜κ的序数α，在M看来都“存在一个α=j（α）与j（κ）之间的不可达基数”，即κ，那么，在V看来也“存在一个α与κ之间的不可达基数”。因此，不可达基数在κ之下是无界的。事实上，任何在Vκ+1中局部成立的大基数性质在κ下都有无界多（unbounded many）的见证。

斯科特在（Scott，1961）中里程碑式的结果是：

定理　4.17　假设存在可测基数，那么V/=L。

证明

假设κ是最小的可测基数，j：V→M是以κ为关键点的初等嵌入，那么M是一个ZFC的传递内模型。而L是最小的内模型，因此，V=L⊂M⊂V，那么，κ在M=V中见证了存在比j（κ）更小的可测基数。由初等性，在V中存在比κ更小的可测基数。这与κ是最小的矛盾了。

这被认为是V/=L的决定性证据，也是第一次从大基数公理直接得到关于自然的数学命题的推论。在下一节中，读者将看到大基数公理未能如哥德尔所愿解决连续统假设问题。但是，索罗维发表于哥德尔诞辰六十周年纪念文集的结果（定理4.15）出人意料地表明，非常高远的大基数公理竟然可以对自然的二阶算术问题做出解答。索罗维在同一篇文章中进一步猜想：假设存在超紧致基数（supercompact cardinal），就可以得到所有投影集的正则性质。

超紧致基数是比可测基数更强的大基数公理。可测基数基于初等嵌入的等价定义为刻画更强的大基数性质提供了一套统一的方式，即通过假设被嵌入V的内模型M与V越来越接近而获得更强的大基数性质。在可测基数的定义中，=Vκ+1，这使得相对于Vκ+1绝对的κ的大基数性质能够被“反射”到κ之下。

定义　4.18（强基数）　对任意基数κ，

（1）令γ是序数。称κ是+γ-强基数（+γ-strong cardinal），当且仅当存在初等嵌入j：V→M，使得crit（j）=κ且Vκ+γ⊂M。

（2）κ是强基数（strong cardinal），当且仅当对任意序数γ，κ是+γ-强基数。

显然，可测基数是+1-强基数。而反过来，任意+γ-强基数都是可测基数。假设κ是+2-强基数，那么κ也是可测基数，而见证它是可测基数的超滤子U∈Vκ+2。利用非平凡初等嵌入的反射论证可以证明，可测基数在+2-强基数下是无界的。

除了通过宣称越来越高的前段相等，刻画M与V非常接近的另一种方式宣称M在足够长的序列下封闭。例如，假设j：V→M是见证κ是可测基数的初等嵌入，可以证明Mκ⊂M，也即M在κ序列下封闭。超紧致基数概念正是推广了这个性质。

定义　4.19（超紧致基数）　对基数κ，

（1）令γ是基数。称κ是γ-超紧致基数，当且仅当存在初等嵌入j：V→M，使得crit（j）=κ且Mγ⊂M。

（2）κ是超紧致基数，当且仅当对任意基数γ，κ是γ-超紧致基数。

显然，对任意序数γ，如果κ是|Vκ+γ|-超紧致基数，那么κ就是+γ-强基数。因此，超紧致基数总是强基数。

与可测基数性质可以被一个超滤子见证类似，每个+γ-强基数κ也可以由一个被称作（κ，|Vκ+γ|+）-延展系统的集合来见证。延展系统（extender）是一系列超滤子，这些超滤子对应的一系列超幂（ultrapower）形成一个直系统（direct system）。一个（κ，λ）-延展系统（κ＜＜λ）往往是Vλ+1中的一个集合。由此，可以利用反射论证证明足够大的δ-超紧致基数下面有许多较小的+γ-强基数。特别地，我们有：

定理　4.20　如果κ是2κ-超紧致基数，那么存在κ个αξ＜κ，使得Vκαξ是强基数。因此，超紧致基数的证明论强度严格强于强基数，即

ZFC+存在超紧致基数⊢Con（ZFC+存在强基数）。

但是，上述定理中的每个αξ未必是V中的强基数，并且一种大基数性质的证明论强度更高也未必蕴涵满足这种大基数性质的基数“更大”。武丁于1984年首次定义的武丁基数（Woodin cardinal）可以作为例证。

定义　4.21（武丁基数）

（1）对任意集合A，称κ是对A的+γ-强基数，当且仅当存在初等嵌入j：V→M，使得

（a）crit（j）=κ且γ＜j（κ）；

(b) Vκ+γ⊂M；(www.daowen.com)

(c) A∩Vκ+γ=j(A)∩Vκ+γ。

（2）称δ是武丁基数，当且仅当对任意A⊂Vδ，存在α＜δ，对任意γ＜δ，α是对A的+γ-强基数。

对A的+γ-强基数可以看作是+γ-强基数的带参数版本。显然，对A的+γ-强基数也是+γ-强基数。因此，如果δ是武丁基数，那么存在α＜δ使得Vδα是强基数。所以，武丁基数的证明论强度严格强于强基数。但同样地，在Vδ看来是强基数的序数在V中未必是强基数。利用反射论证甚至可以证明：

定理　4.22　假设δ是武丁基数，κ＜δ是强基数，那么存在κ个＜κ的武丁基数。

因此，如果同时存在武丁基数和强基数，那么第一个武丁基数必然小于第一个强基数——尽管武丁基数是更强的大基数性质。利用反射论证甚至可以证明：第一个武丁基数自身不是可测基数（尽管仍然有许多可测基数在其下）。

大基数的“大”往往来自于相应的大基数性质允许我们使用越来越强的反射论证。其背后的直观是：集合论宇宙V的广大可以不断超出人们的想象。人们每每自以为以某种方式可以刻画了集合论宇宙V，他们所刻画的其实都只是集合论宇宙的某个前段Vκ。正是基于这个直观，康托尔将集合论宇宙称作绝对无穷并暗示其不可理解性。而哥德尔称（Gödel，1964，p. 260），“……的集合”算子（the operation “set of”）可以被不断迭代，而大基数公理正是对这种极大性的刻画：

从一个某种意义上与此^[16]截然相反的公理出发，也许能推出康托尔猜想不成立。我这里所想的公理或许会谈到某种关于所有集合组成的系统的极大性（类似于几何里的希尔伯特完备性公理），而公理A 【即V=L】谈论的则是极小性。注意只有某种极大性才似乎能与……集合概念相融合。（Gödel，1964，pp.262–263）

因此，大基数公理被认为可以获得某种内在性辩护而被许多集合论学家接受为ZFC公理系统的典范扩张。

回到第162页的索罗维定理4.15。该定理的意义在于让人们意识到，大基数公理不仅能将证明论强度的典范层谱推广至ZFC之上，还能在具体的二阶算术领域给出直接的推论。这些推论不仅仅是诸如公理系统一致性这样的元数学命题，而且包括数学分析学家们所关心的自然的数学命题。由于集合的决定性蕴涵集合的正则性质（定理4.11），人们有理由期待大基数公理可以直接证明决定性从而让所有正则性质有一个统一的解决方案。马丁很快便在（Martin，1970）中给出了正面答案。

定理　4.23（马丁1970）假设存在可测基数，那么所有集合都是被决定的。

更进一步的正面结果直到1980年才由马丁再次证明。

定理　4.24（马丁1980）假设I2（见定义4.29），那么所有集合都是被决定的。

I2是非常强的大基数性质，已经很接近不一致了。武丁在1984年由已知最强的大基数性质证明了决定性公理对所有可构成集成立。

定理　4.25（武丁1984）　假设I0（见定义4.29），那么ADL（R）。

最强的大基数性质

利用初等嵌入j：V→M定义的大基数性质随着要求M与V越来越接近而获得越来越强的反射性质。一个自然的想法是：假设M=V就可以得到上述意义下最强的大基数性质。莱因哈特（Reinhardt，William Nelson）在他博士论文（Reinhardt，1967）的末尾刻画了这个大基数性质。

定义　4.26（莱因哈特基数）　莱因哈特基数（Reinhardt cardinal）是非平凡初等嵌入j：V→V的关键点。

然而，库能很快证明了莱因哈特基数性质与ZFC不一致（Kunen，1971）。库能和后来各种改良版的证明都不可避免地使用了选择公理。虽然许多集合论学家猜想，莱因哈特基数与ZF已经矛盾了，但至今尚未被证明。为此，武丁在90年代初期的一次讨论班上定义了一种更强的大基数性质，试图将莱因哈特基数不一致证明的关键步骤更明显地暴露出来。

定义　4.27（伯克利基数）　κ是伯克利基数（Berkeley cardinal），当且仅当对任意传递集M满足κ∈M都存在非平凡初等嵌入j：M→M且crit（j）＜κ。

然而，伯克利基数与ZF的一致性目前仍未可知。

另一方面，库能的结果可以被推广为：

定理　4.28（库能）　假设ZFC。对任意δ，不存在非平凡初等嵌入j：Vδ+2→Vδ+2。

这提示了一种定义恰好在不一致以下的大基数性质的方式。

定义　4.29（阶到阶的）　基数λ是阶到阶的（rank-intorank），当且仅当它满足下述某个性质：

I3存在非平凡初等嵌入j：Vλ→Vλ；

I2存在非平凡初等嵌入j：V→M，满足Vλ⊂M且λ是最小的＞crit（j）的固定点，即j（λ）=λ；

I1存在非平凡初等嵌入j：Vλ+1→Vλ+1；

I0存在非平凡初等嵌入j：L（Vλ+1）→L（Vλ+1）且crit（j）＜λ。

“阶到阶的”中的阶就是指冯·诺伊曼层谱的阶。从I3到I0，反射性质在不违反定理4.28的前提下被逐渐加强，因此（证明论）强度也越来越强。阶到阶的性质是目前被集合论学家刻画的且未被证明与ZFC矛盾的最强的大基数性质。

然而，无论I0还是I2都被认为是过强了。内模型计划（参见第179页）在当时看来似乎毫无做到这些大基数性质上的希望。因此，接下来的问题是如何有效降低所需的大基数假设。据报道（Kanamori，2003，p.461），武丁在1984年4月给出了从超紧致基数到所有可构成集都是勒贝格可测的证明。他在当年访问耶路撒冷期间定义了武丁基数并与谢拉合作证明了下述定理：

定理　4.30（谢拉-武丁）如果存在无穷个武丁基数以及一个可测基数在它们之上，那么L（R）中的每个实数集都是勒贝格可测的。

类似地，人们会希望这个结果能推广到决定性上。1985年9月，专注于内模型计划的马丁和斯提尔（Steel，John Robert）发现将内模型推广至武丁基数的困难可以被用来证明决定性（Martin and Steel，1989）。^[17]

定理　4.31（马丁-斯提尔）　假设存在n个武丁基数以及一个可测基数在它们之上，那么所有集合都是被决定的。因此，如果存在无穷个武丁基数，那么PD成立。

武丁稍后又将该定理推广到证明所有可构成集的决定性。

定理　4.32（马丁-斯提尔-武丁）　假设存在无穷个武丁基数以及一个可测基数在它们之上，那么ADL（R）成立。

武丁的下述定理表明，马丁和斯提尔的结果已经是最佳结果了。有穷个武丁基数不足以证明PD或ADL（R）。

定理　4.33（武丁）　下述理论是等一致的：

（1）ZFC+存在无穷个武丁基数；

(2)ZF+AD。

根据之前的介绍，武丁基数是相对阶到阶的大基数性质或超紧致基数弱得多的大基数性质。马丁、斯提尔和武丁的成果无疑是重大的突破。马丁和斯提尔后来将内模型计划推广至武丁基数的武丁基数极限（在一个关于迭代树在极限处可迭代的假设下），这为武丁基数的一致性提供了有力的证据。一些集合论学家就此认为，武丁基数存在，并且PD和ADL（R）是集合论真命题。

PD或ADL（R）成立的另一个证据来自于所谓的外在性辩护。哥德尔在其哲学论文《康托尔篇》（What is Cantor’s Continuum Problem，Gödel，1964）中试图解释这种辩护：

即使不考虑新公理的内在必然性，甚至它完全没有内在必然性，仍旧可能通过另一种方法来大致决定其真假，即归纳地研究新公理的“功效”。这里的功效指的是其推论的丰富性，……可能存在一类公理，它们有如此众多可验证的推论，能使整个领域变得如此明晰，并且能产生如此强有力的解决问题的方法（甚至构造性地解决问题，只要有可能），那么无论它们是否具有内在必然性，我们都不得不至少像对已经确立的物理理论那样接受它们。（Gödel，1964，p.261）

“推论的丰富性”的追求在当代集合论中被更具体地刻画为理论的实际完备性。由于大基数公理被认为是ZFC证明论强度的典范扩张，为集合论寻找新公理的任务就被转换为在诸多等一致的公理候选中挑选最似真的。然而，集合论中被用来证明相对一致性的常见方法只有内模型方法和力迫法。因而，如果某个理论在一定领域内的推论无法被内模型方法和力迫法更改，就可以称该理论在该领域内是实际完备的。另外，根据哥德尔的极大性质原则（见第167页），在脱殊扩张中成立的往往比在内模型中成立的命题获得更强的内在性辩护。所以，在追求实际完备性的过程中，考虑所有的脱殊扩张似乎就足够了。

根据拉尔森（Larson，Paul Bradley）的报道（Larson，2004），武丁在1985年的手稿中证明了下述定理：

定理　4.34（武丁）假设存在任意大的武丁基数，那么L（R）的理论在所有集合力迫的脱殊扩张中不变。即对任意集合论句子σ，任意集合偏序（P，≤，1）有，

σL(R)↔(1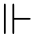σL(R))。

也就是说，大基数公理的确如哥德尔所愿具有“推论的丰富性”。特别地，ZFC+大基数公理在二阶算术乃至L（R）理论上是实际完备的。显然，在这个实际完备的理论中，ADL（R）成立。武丁的另一个定理表明，几乎任何关于L（R）实际完备的理论都蕴涵ADL（R）。

定理　4.35（武丁）　假设存在任意大的不可达基数并且L（R）的理论在所有集合力迫的脱殊扩张中不变，那么ADL（R）。

“存在任意大的不可达基数”已经是非常弱的大基数性质，任何集合论实在论者都会认为这是关于集合论宇宙的简单事实。而如果他们希望得到实际完备的的二阶算术理论，他们就必须承认投影集决定性公理。对实在论者来说，当代集合论已经近乎完美地解决了所有二阶算术中自然生成的独立性问题。关于大基数理论与决定性公理更详细的介绍可以在（Kanamori，2003）中找到。在下一节中读者将看到在二阶算术中顺利推进的哥德尔纲领（Gödel’s program）却如何在以连续统假设问题为代表的三阶算术上困难重重。