描述集合论考虑的是可定义的实数集及其性质。当我们跟随幂集公理逐渐深入无穷的王国，在选择公理的作用下会发现一系列匪夷所思的现象。利用选择公理，可以证明存在不可测的集合，而后者的存在使得巴拿赫-塔斯基悖论（Banach-Tarski paradox）得以可能。巴拿赫-塔斯基悖论实际上是ZFC的定理，可表述为：可以把一个三维实心球体分解为有穷多个部分，并只通过旋转和平移重新组成两个和原球体相同体积的球体。该定理过于违反直观以至于被称作“悖论”。实际上，被切分出来的诸子集不是可测的集合，无法将通常的体积概念应用于这些集合，才会出现违反直观的情况。由于上述定理必须用到被认为是非构造的选择公理，人们似乎有理由期望，至少那些可定义的实数集不会出现这种糟糕的属性。

在描述集合论中，有一组较好的属性被称作正则性质。常见的正则性质有：（1）勒贝格可测（Lebesgue measurable）性、（2）完美集性质（perfect set property）和（3）贝尔性质（Baire property）。如果一个实数集是勒贝格可测的，我们可以按照一个统一的标准赋予它一个测度来表示它的长度、面积或体积，并且当我们将它与其他集合（包括对它进行平移得到的集合或与其他集合的交或差）比对时，这个统一的测度不会出现不一致（例如巴拿赫-塔斯基悖论的情况）。一个实数集具有完美集性质，那么它要么是可数的，要么与连续统是等势的，也即无法作为否定连续统假设的反例。贝尔性质的直观是：一个集合非常接近于开集。^[8]

正则性质

在数学分析中，人们希望有一套统一的标准来测量欧式空间中任意子集的长度、面积、体积等。以直线R为例，闭区间[a，b]的长度ℓ[a，b]可以自然地定义为（b-a），那么单点集[a，a]的长度就是ℓ[a，a]=0，而开区间（a，b）的长度与闭区间[a，b]的一样：ℓ（a，b）=ℓ[a，b]=（b-a）。对于更复杂的集合，我们希望它们上面的测度μ是对上述长度函数的推广且至少满足下述性质：

（1）如果X⊂Y，那么μX≤μY（单调性）；

（2）假设{Xn}n＜ω是可数个两两不交的集合，那么

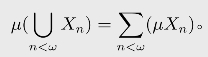
（可数可加性）；

（3）对集合X、实数r，令（X+r）={x+r|x∈X}，则

μX=μ(X+r)

（平移不变性）。

为了将之前的测度推广至一般集合，可以定义下述外测度（outer measure）概念：

定义　4.1（外测度）　对任意X⊂R，定义X的外测度μ*（X）为

换句话说，一个集合的外测度是它的所有开覆盖（可数个开区间的并）测度的下确界。显然，外测度是区间长度函数的扩张，并且满足单调性和平移不变性。但是，外测度在一般集合上只满足准可数可加性：μ（∪n＜ωXn）≤∑n＜ω（μXn）。由此可以证明，任何可数集合的外测度都是0。因此，任意在[0，1]区间中取一个点，取到有理数的概率是0。

利用选择公理，我们可以构造外测度可数可加性的反例。考虑区间[0，1]中元素间的等价关系：

a～b⇔（a-b）是有理数，

由此，可以把[0，1]中的实数划分为2ℵ0那么多个等价类（显然，每个等价类都是可数的）。由选择公理，从每个等价类中选取一个实数组成一个实数集V。我们称V是一个维塔利集（Vitali set）。对V做有理数距离的平移可以得到一系列与它具有相同外测度的集合（V+q）。并且，有理数q /=r，那么（V+q）∩（V+r）=Ø。令〈qn〉n＜ω枚举所有[-1，1]中的有理数。考虑集合

容易证明，[0，1]⊂U⊂[-1，2]。由单调性，1≤μ*（U）≤3。由准可数可加性，

因此，维塔利集V的外测度不是0。而可数无穷个非零测度加起来是∞，因而μ*U≤3＜u=∞，可数可加性不成立。外测度甚至不满足（有穷）可加性。假设对有理数q /=r有

那么就可以归纳地证明对任意N＜ω有

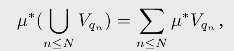
取N使得等式右侧的值＞3就导致矛盾了。

一个自然的想法是：当考虑集合的测度时，排除像维塔利集这样糟糕的集合。

定义　4.2（勒贝格可测集）　我们称一个实数集X是勒贝格可测的，当且仅当X满足卡拉西奥多里标准（Carathéodory criterion）。即，对任意实数集A，有

μ*(A)=μ*(A∩X)+μ*(A\X)。

显然，不满足可加性的维塔利集不满足卡拉西奥多里标准。可以证明，如果把外测度限制在勒贝格可测的集合上，那么可数可加性也成立。并且，可以证明勒贝格可测集在取补集和可数并下封闭。也就是说，勒贝格可测集组成了一个σ-代数（σ-algebra）。

定义　4.3（完美集）

（1）称一个集合X是完美集，当且仅当X是闭集且不含有孤立点；

（2）集合X具有完美集性质，当且仅当X要么是可数的，要么包含一个非空的完美集。

可以证明，在任何非空完美集中都可以嵌入一个康托尔空间2ω，因而非空完美集与整个连续统等势。那么，一个具有完美集性质的集合无法见证存在基数上严格小于连续统的不可数集合。

康托尔与本迪克森（Bendixson，Ivar Otto）证明了所有闭集都具有完美集性质。但并不是所有集合都具有完美集性质。由于实数上的闭集有连续统那么多个，可以令〈Cξ〉ξ＜2ℵ0枚举所有不可数闭集（需要选择公理）。每个Cξ都具有完美集性质，因而基数也都是2ℵ0。因此，可以递归地从每个Cξ中取出尚未出现的一对实数（xξ，yξ）。令X={xξ|ξ＜2ℵ0}，则xξ见证了X与每个不可数闭集Cξ相交，而yξ见证了每个Cξ不是X的子集。我们称这样的集合为伯恩斯坦集（Bernstein set）。显然，伯恩斯坦集不具备完美集性质。此外也可以证明，伯恩斯坦集与每个正测度的勒贝格可测集相交而不包含任何一个，因此伯恩斯坦集是不可测的。

定义　4.4（贝尔性质）

（1）实数集X是无处稠密的，当且仅当在任意非空开集U中都可以找到一个子开集V避开X，即V∩X=Ø；

（2）实数集X是贫集（meager set），当且仅当X可以被表示为可数个无处稠密集合的并；

（3）实数集X具有贝尔性质，当且仅当存在开集U，使得X △U是一个贫集。

无论无处稠密的集合还是贫集，直观上都是非常稀疏的集合。例如，整数集在实数中就是无处稠密的；有理数集是稠密的，也是贫集。贝尔性质所说的就是：一个集合与一个开集只差一个非常稀疏的集合。因此，具有贝尔性质的集合又被称作“几乎开的”。

容易证明，贝尔性质也对σ-代数封闭。而伯恩斯坦集同样与每个具有贝尔性质的非贫集相交而不包含任何一个，因此并非所有实数集都具有贝尔性质。

利用选择公理，人们很容易找到上述正则性质的反例。但是通过选择公理得到的反例被认为并非构造性的。例如，并没有什么一致的方法能让人判断一个实数是否属于一个维塔利集。另一方面，人们所熟悉的集合几乎全部具有正则性质。例如，所有的开集、闭集都是勒贝格可测的，具有完美集性质和贝尔性质。事实上，具有这些正则性质的集合在取补集和可数并下封闭，也即组成了一个σ-代数。这说明，满足这些正则性质的集合也是相当丰富的。因此，有理由猜测，是不是所有可定义的实数集都具有正则性质？(www.daowen.com)

为了更方便地刻画可定义性及其层谱，集合论学家一般把ωω={f|f：ω→ω}作为实数集。在ωω上存在一个自然的拓扑：对任意有穷序列σ∈ω＜ω，取它的所有无穷尾节扩张[σ]≺={f∈ωω|σ≺f}，则以

作为拓扑基生成的拓扑空间称作贝尔空间（Baire space）。贝尔空间与直线上的序拓扑空间并不同胚（例如，后者是连通的而前者不是），但就描述集合论所关心的可定义性与正则性质而言，并不没有什么不同。此外，贝尔空间有一些更方便的属性。例如，每个[σ]≺都是既开又闭的。

波莱尔集（Borel set）被定义为由开集通过补集和可数并生成的集合。具体而言，可以递归地定义波莱尔集层谱如下：

定义　4.5（波莱尔集层谱）　对α＜ω1，递归定义集合：

（1）定义所有开集为的；

（2）称集合X为的，当且仅当它的补集ωω\X是的；

（3）对α＞1，集合X是的，当且仅当存在集合序列〈Xi〉i＜ω使得X=∪i＜ωXi，其中每个Xi都是某个集合且βi＜α；

（4）如果X既是也是的，那么称X是的。

显然，如果α＜β，那么类似地，。因此，波莱尔集可以被等价地定义为中的集合，也即波莱尔集组成包含开集的最小σ-代数。波莱尔集层谱如图4.2所示。

图4.2　波莱尔集层谱

运用对角线法可以证明，图4.2中的子集符号都是真子集关系。

在波莱尔集之上，鲁金（Luzin，Nikolai）与他的学生苏斯林（Suslin，Mikhail Yakovlevich）在（Lusin，1917）和（Suslin，1917）中引入了分析集（analytic set）概念。集合A是分析集当且仅当它是一个波莱尔集的投影，即存在波莱尔集B⊂（ωω）n+1，使得^[9]我们称一个集合是余分析集，当且仅当它的补集是分析集。苏斯林证明了，一个集合是波莱尔集，当且仅当它既是分析集也是余分析集。运用投影运算推广分析集就得到了投影集层谱（projective set hierarchy）。

定义　4.6（投影集层谱）　对n＜ω递归定义集合：

（1）定义分析集为的；

（2）集合X⊂（ωω）n是的，当且仅当存在集合Y使得，X=（ωω）n\Y；

（3）集合X⊂（ωω）n是的，当且仅当它是某个集的投影，即存在的集合Y⊂（ωω）n+1，使得

（4）集合X是的，当且仅当它既是的也是的。

显然，的集合就是余分析集，而集就是波莱尔集。投影集层谱的图像与波莱尔集层谱类似。容易证明，需要注意的是，投影集层谱指对每个自然数n有定义，而波莱尔集层谱对任意可数序数α有定义。

逻辑学家常用表示谓词逻辑公式以及由这种公式定义的集合的复杂程度。其中，上标n表示该公式最高阶量词是几阶的。0表示一阶的，往往是以自然数集N或Vω=HF为辖域，1表示二阶的，以P（N）或Vω+1或HC为辖域。依此类推。而下标m提示该公式最高阶量词前置后，存在与全称量词交替叠置的次数。例如，公式具有∃x1...∃xkφ的形式，公式则形如而∃x∀y∃zθ可能是一则的公式。

用类似的符号来标记波莱尔集层谱与投影集层谱，是因为两者确实与定义复杂性的层谱有关。事实上，一个投影集是的，当且仅当存在一个以实数为参数的二阶算术的公式定义它。之所以用粗体符号来表示投影集层谱，是为了与不带参数的可定义性作区分。后者被称作分析层谱（analytical hierarchy），它是自然数集算术层谱的推广，是投影集层谱的无参数版。细体字版波莱尔集层谱（lightface Borel hierarchy）就是不带参数的波莱尔集层谱。细体字版的波莱尔集又被称作能行版的波莱尔集，其层谱只定义到丘奇-克莱尼序数（Church-Kleene ordinal），对应于自然数集的超算术层谱（hyperarithmetical hierarchy）。

投影集层谱还可以继续推广至可构成集层谱。参照定义3.9，令L0（R）=dfVω+1，Lα+1（R）=dfD（Lα（R）），Lα（R）=df∪ξ＜αLξ（R）（若α是极限序数），L（R）=∪α∈ONLα（R），那么，L1（R）中含的实数集恰好是投影集，而Lα（R）∩P（R）则形成实数集的可构成集层谱。

波莱尔集层谱、投影集层谱和可构成集层谱基本囊括了描述集合论所关心的“可定义的”实数集。这些可定义实数集的性质，几乎都能（通过编码）在二阶算术结构Vω+1或HC中表达。

作为二阶算术的描述集合论

描述集合论考虑的对象是一些实数集。如果我们将自然数作为一阶算术的对象，实数作为二阶算术的对象，那么实数集就是三阶算术的对象。但另一方面，如果只考虑“可定义的”实数集，就有可能将这些三阶对象编码为实数（二阶对象）。

在贝尔空间ωω中，基本的开闭集[s]≺作为一个实数集所包含的信息完全可以编码为一个遗传有穷集合s或一个自然数n（s）。给定实数x，x∈[s]≺当且仅当x↾|s|=s，而后者可以被表示为算术公式θ（x，n（s））。一个开集可以表示为可数个基本开闭集的并：U=∪i＜ω[si]≺。令实数f∈ωω编码序列〈si〉i＜ω，即f（i）=n（si），那么，x∈U就可以用算术公式∃iθ（x，f（i））来表示，或记作以x，f为参数的二阶算术公式η1（x，f）。由此，我们可以避免直接谈论[s]≺或U这些三阶算术的对象。类似地，可以递归定义每个集类的编码模式，即公式ηα，使得对任意X∈，存在X的编码∈ωω，使得对任意实数x∈X当且仅当ηα（x，fX）。又由于ηα是由α＜ω1“能行地”得到的，因而可以一般地编码波莱尔集。即存在二阶算术公式β，使得对任意波莱尔集X，存在它的编码bX，有对任意x∈X当且仅当β（x，bX）。

一个分析集是一个波莱尔集的投影。所以，任给分析集A，存在波莱尔集B，使得对任意实数x，x∈A当且仅当存在实数y满足（x，y）∈B。因此，x∈A可以表示为以x和bB为参数的公式：∃yβ（（x，y），bB）。由此，几乎所有的描述集合论问题都可以被翻译为关于二阶算术结构Vω+1或HC中的问题。

经过上述澄清，现在的问题是：是否所有的波莱尔集、投影集甚至可构成集都满足上述三条正则性质？我们已经知道所有的开集、闭集都具有全部正则性质。并且容易看出，勒贝格可测性和贝尔性质在σ-代数下封闭，波莱尔集都是勒贝格可测的且有贝尔性质。鲁金和苏斯林于1917年证明了下述ZFC定理：

定理　4.7（鲁金-苏斯林）　任意分析集（集）都具有完美集性质、贝尔性质并且是勒贝格可测的。

接下来的的问题是：这些结果能否推广到投影集，甚至可构成集？然而，哥德尔1938年的发现表明，鲁金与苏斯林的成果已经是ZFC中可以证明的最佳结果了。

哥德尔在（Gödel，1938）中陈述的定理除了人们熟知的连续统假设和选择公理相对ZF的一致性，还包括：

（1）存在的不可测集；

（2）存在不满足完美集性质的集是相对ZFC一致的。对可构成集类L的构造更细致的分析可以发现，其中存在一个可定义的实数集ωω上的良序，由此可以构造出三种正则性质的的反例。所以，如果ZFC是一致的，那么ZFC证明不了集合具有正则性质。

另一方面，索罗维在1965年（Solovay，1965）宣布了下述定理（证明发表在（Solovay，1970））：

定理　4.8假设（ZFC+存在不可达基数）^[10]一致，那么存在V的脱殊扩张V[G]，在其中所有以可数序数序列为参数可定义的实数集都是勒贝格可测的且具有完美集性质和贝尔性质。特别地，在L（R）V[G]中，所有实数集都是勒贝格可测的且具有完美集性质和贝尔性质。

也就是说，如果（ZFC+存在不可达基数）一致，那么ZFC也证明不了有投影集或可构成集不具备正则性质，ZF证明不了任何集合不具备正则性质。^[11]

根据（Stillwell，2010，p. 180）的报道，鲁金在1927年宣称

人们不知道，且人们将永远不知道

是否所有投影集是可测的且具有完美集性质。这看似与希尔伯特的著名口号（见第2页引文）针锋相对，但其实反映了当时的分析学家对自己直观的自信：既然尝试了所有方法都无法证明，那么一定是不可证的。哥德尔和索罗维的结果在一定意义上验证了鲁金的预言，投影集是否具有正则性质至少是ZFC无法回答的。

分析学家的直觉的确令人惊叹，但集合论学家并未就此止步。在接下来读者将看到，集合论学家如何诉诸对集合论宇宙的直观来判定这些二阶算术命题的真假。^[12]