极端的怀疑论会面临太多的不方便。形式主义者试图回避谈论数学命题的真假，但仍然要求证明他们的数学游戏是一致的。后者被翻译为一则数学命题Con（T），形式主义者不仅要求对Con（T）的一个证明，还要求它是真的。妥协的结果是：形式主义接受“某个层次”以下的数学作为元理论是客观的，而更“高阶”的数学则只是façon de parler（说话方式）。同理，反对实无穷的学者大多至少接受自然数结构是客观的。

在集合论中，定义HF为所有遗传有穷集合（hereditarily finite set）组成的类。如果我们追溯一个集合X的元素、元素的元素、元素的元素的元素……只能得到有穷个不同的元素，那么我们称X是遗传有穷的。严格地，定义一个集合的传递闭包trcl X为最小的包含X并且在∈的逆下封闭的（即若a∈trcl X且b∈a，则b∈trcl X）集合，则HF={X|card（trcl X）＜ω}。在基础公理下可以证明，HF=Vω。^[4]因此，HF是一个集合。事实上，HF中的集合就是那些包含且仅包含（如何从Ø构造出来的）有穷信息的集合。利用莫斯托夫斯基函数（Mostowski function），我们可以构造（HF，∈）理论与自然数结构（N，+，·，0，1）理论（一阶算术）之间的相互翻译。^[5]每个遗传有穷集合（的全部信息）被编码为一个自然数。

莫斯托夫斯基函数

对Vω中元素a递归定义：

显然，Mf（Ø）=0。而对集合a={b1，...，bk}，Mf（a）=2Mf（b1）+···+2Mf（bk）。也就是说，编码集合a的自然数Mf（a）的二进制展开在第Mf（bi）位（1≤i≤k）上是1（见图4.1）。

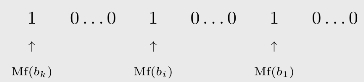
图4.1　Mf（a）的二进制展开

因此，HF的理论就是集合论学家的一阶算术理论。集合论中有一定争议的幂集公理和选择公理在HF=Vω里都是平凡成立的，关于无穷的一切魔法从Vω+1开始发生。Vω+1=P（Vω）包含了所有自然数子集（即集合论学家的实数）作为其元素。（Vω+1，∈）是集合论学家的二阶算术模型，它的理论与完全二阶算术结构（N，P（N），+，·，0，1）的理论是可以相互翻译的。此外，定义HC为所有遗传可数集合（hereditarily countable set）组成的集合（Vω+1⊂HC⊂），可以证明（HC，∈）与（Vω+1，∈）的理论也是可以相互翻译的（每个遗传可数的集合可以被“编码”为一个自然数子集）。有时候，集合论学家更喜欢将（HC，∈）作为二阶算术模型。

整个Vω+1的基数已经等于连续统的基数，是不可数的了。也就是说，如果我们的语言是可数的，那么一定有二阶算术的对象是不可定义的。将这些不可定义的对象引入数学王国引起许多数学家的反对。有穷主义者往往只承认原始递归的对象，而直谓主义者只承认在一阶算术结构（Vω，∈）中可定义的集合。这些构造主义者的担心并非杞人忧天。(www.daowen.com)

在集合论宇宙中，HF的结构是非常坚固、难以被改变的。对任意集合论的传递模型M，N（无论M，N是集合模型还是类模型），其中的遗传有穷集是固定的：HFM=HFN。^[6]而不同集合论模型却可能含有不同的实数。例如，可构成集类L中的实数都是可构成的。利用科恩力迫（参见定义3.16），我们可以添加任意多个“新”的实数，这些实数不是可构成的，其数量可以使连续统假设为假。又如，利用萨克斯力迫（Sacks forcing）我们可以“生成”一个可构成度极小的不可构成实数a，使得对任意实数r∈L[a]，要么r∈L，要么a∈L[r]。也就是说，a是复杂度最小的不可构成实数，对任意不可构成的实数r都有a∈L[r]。二阶算术的对象Vω+1在这个意义上并不是一个坚固的结构，而是可以轻易被改造的结构。或者说，人们似乎很容易想象不同的Vω+1而难以断定哪个才是真实的。这让怀疑论者断言根本不存在所谓唯一真实的二阶算术结构。

即使可能有不同的结构，人们仍然可以期望这些结构的理论是一样的。对本体论的实在论的否定未必蕴涵对真的客观性的否定。例如，自然数的诸多非标准模型之间可以是初等等价的，具有同样的一阶算术理论。在一些情况下，我们可能无法在这些算术模型中确定哪一个才是真实的。但这不影响我们判断一个算术命题的真假。一则算术命题是真的，当且仅当它在其中一个也即所有模型上真。本章中将反复谈及的脱殊多宇宙观（generic multiverse view）正是这种哲学立场的具体表现。

如果只考虑理论，哥德尔不完备性定理的确告诉我们，即使一阶算术的理论也不是坚不可摧的：一阶算术的任何一致的公理系统都是不完备的。例如，令ZFCN为所有ZFC可证的一阶算术命题组成的理论。它比皮亚诺算术等常见算术公理系统要强很多，比如，它含有Con（PA）。但如果ZFC是一致的话，Con（ZFC）是独立于ZFCN的。

目前集合论中已知的证明一致性（即不可证性）的方法只有：（1）哥德尔不完备性定理及其衍生；（2）内模型方法；以及（3）力迫法。利用哥德尔不完备性定理直接给出的独立命题往往被认为是人为的、不自然的。此外，根据定义3.5所定义的理论间证明论意义上的等价关系，可以将各个理论和公理系统划分为不同的证明论强度；再根据定义3.2所定义的（严格）强弱关系◁，我们可以将至少包含有穷主义算术的公理系统按照证明论强度排列成一个偏序关系。在一定的一致性假设下，可以证明这个序结构是可以不断向上分叉的。换句话说，这个序结构既不是线性的，也不是良基的，而是一个纷繁复杂的结构。但是，一个值得注意的现象是，工作中的数学家们实际会用到的数学公理系统，从严格有穷主义算术、皮亚诺算术、二阶算术、类型论、集合论到大基数等，在证明论强度意义上几乎排列成了一个良序，即哥德尔层谱（见第49页）。对实在论者来说，已有的哥德尔层谱是一条不断强化公理系统的正确途径，只是这条路径尚不足以得到足够完备的公理系统来判定一些人们关心的数学命题。例如，在第三章中，我们实际证明了ZFC+CH和ZFC+¬CH属于同一个证明论强度，所以，对集合论的实在论者来说最关切的问题是如何在属于同一个证明论强度而相互排斥的命题间做出选择。这种命题对的存在性目前只有通过内模型方法或力迫法来证明。因此，如果关于某类结构的理论能够免于这两种方法的改变，我们就可以称该理论是实际完备的（effectively complete）。

容易证明，不同ZF传递模型的一阶算术理论是绝对的。即：对任意一阶算术命题σ^[7]，有

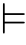特别地，用内模型和力迫法生成的ZFC模型都不改变传递性。因此，这两种方法都无法左右一阶算术命题的真假。在这个意义上，一阶算术在集合论中是实际完备的。而这点在二阶算术上就未必成立了。假设M是L的萨克斯力迫扩张，那么HCL“所有实数都是可构成的”，而HCM“存在不可构成的实数”。这些独立的二阶算术命题是否有确定的真假？如果有的话是真还是假？对这些问题的回答不可避免地要诉诸数学证明以外的论证，或可称作哲学的论证。

接下来，我们以对描述集合论的一些研究为例来说明当代集合论学家如何结合纯数学的工作和哲学的论证试图判定二阶算术命题的真假。