哥德尔证明了连续统假设的相对一致性。即：如果ZFC是一致的，那么我们是无法在ZFC下证明连续统假设是错的。然而，哥德尔并没有就此倾向于认为连续统假设成立。相反，哥德尔根据他对集合论宇宙的直观，自发现连续统假设的相对一致性以来就坚信连续统假设的否定也是相对一致的。可以说，科恩的证明对哥德尔来说并没有带来哲学上的惊喜或冲击。^[23]但是，科恩的方法是开创性的，甚至如其所言一度使人产生哲学上的困惑。

集合论的柏拉图主义者（Platonist）认为，诸集合是以某种方式客观存在的，它们组成了唯一的囊括所有的极大的集合的宇宙，而集合论就是关于这一客观的宇宙的理论。内模型方法与这种观点可以很好地兼容。可构成集集类L无非是通过定义划出的一类集合。在其中，人们发现并没有很多自然数集的子集，因而连续统假设成立。然而，我们已经知道内模型方法是无法得到¬CH的相对一致性的。既然内模型不行，一个很自然的想法便是诉诸“外模型”。特别地，如果说内模型的方法是通过将自然数集ω的子集限制为可构成集而得到CH成立的情况，那么我们同样可以通过添加足够多的ω的子集来得到CH为假的情况。但是，按照柏拉图主义者的观点，那个唯一的集合论宇宙必须是极大的，如果我们还可以想象比它更大的宇宙，那么我们的集合概念就是不一致的了。

但请注意，我们要证明的是形如

Con(ZFC)→Con(ZFC+¬CH)

的相对一致性。我们可以假设Con（ZFC），也即假设存在ZFC的（集合）模型。根据勒文海姆-斯寇伦定理（Löwenheim-Skolem theorem），就存在一个ZFC的可数模型。人们常称这些集合论的集合模型，尤其是可数模型为玩具模型（toy model）。这些玩具模型本身是集合论宇宙中的一个很小的集合。谈论往玩具模型中添加新的集合使得由此得到的扩张了的模型满足ZFC和¬CH，就显得很自然了。即：我们通过假设存在一个ZFC模型，证明了存在（ZFC+¬CH）的模型，并由此证明了上述相对一致性命题。

勒文海姆-斯寇伦定理

定理　3.13（勒文海姆-斯寇伦）给定基数为κ的一阶语言L以及无穷L结构M，那么对任意基数λ ≥κ，存在基数为λ的L结构N，使得要么存在从N到M中的初等嵌入（elementrary embedding），要么存在从M到N中的初等嵌入。

集合论语言是可数的一阶语言，因此，如果存在一个ZFC模型，那么就存在任意基数的ZFC模型。

特别地，假设（M，E）是ZFC的可数模型。由于（M，E）是ZFC的模型，其中自然也有不可数的基数，不妨将（M，E）中被认为是第一个不可数基数的对象记作，第二个记作，等等。但是，M本身是一个可数的集合，所以（M，E）能看到的中的对象{x∈M|（M，E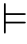）x∈}是M的一个子集，因而是至多可数的。另一方面，我们知道，ω的子集有不可数多个，即P（ω）≥ℵ1^[24]，那么，我们似乎只需要往M中添加足够多的“ω的子集”就可以骗过（M，E），令其认为它里面“ω的子集”有超过那么多个就可以了。

斯寇伦悖论

根据勒文海姆-斯寇伦定理，如果存在ZFC模型，那么就存在可数的ZFC模型。又或者ZFC可以直接证明存在可数模型满足ZC和足够强的替换公理模式。无论ZFC还是ZC都可以证明存在不可数的集合。斯寇伦（Skolem，1922）首次指出这一看似悖论的现象：

据我所知，尚未有人注意到这一特别的显然矛盾的事态。凭借这些公理，我们可以证明存在更高的基数，更高基数的类，等等。那么又怎么会出现整个论域B本身早就是可以被有穷正整数枚举的情况呢？（Skolem，1922，p. 295）

斯寇伦将斯寇伦悖论（Skolem’s paradox）作为他反对公理化集合论作为数学基础的理由，因为一阶理论无法唯一地决定论域。今天集合论学家已经有成熟的方法来处理斯寇伦悖论以及其他集合论模型间不满足绝对性（absoluteness）的现象（见第127页）。

然而，上述分析仍然有一些不严谨的地方。模型（M，E）中的二元关系E未必是集合论宇宙上的属于关系，因此，集合{x∈M|（M，E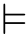）x∈}={x∈M|}未必等于，甚至也未必等于M∩={x∈M|x∈}。作为集合论宇宙中的一个对象本身可能是个不可数的集合，甚至任意一个集合；而集合{x∈M|（M，E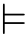）x∈}却有可能并不属于M。

另一方面，（M，E）当然认为其中存在一个自然数集，记作ωM。类似地，ωM作为集合论宇宙中的对象可能是任意一个集合，而被M当作自然数的对象组成的集合{x∈M|（M，E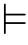）x∈ωM}可能不属于M。更重要的是，集合{x∈M|（M，E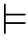）x∈ωM}及其上的E的关系可能并不与集合论宇宙中真正的自然数上的序关系（ω，∈）同构。（M，E）中的自然数序可能是一个非标准模型。

上述种种使得生活在真正集合论宇宙（V，∈）中的人与生活在（M，E）中的人之间的对话非常困难。在（V，∈）中的人难以判断该加入多少自然数子集才能令（M，E）中的人相信有足够多了；在（V，∈）中的人甚至也难以判断到底什么样的对象能被（M，E）是识别为自然数的子集。尽管（M，E）原则上是可以被（V，∈）理解的，但有关操作会变得异常复杂。

一种理想的解决方案是将（M，E）同构于（V，∈）的一个子结构（M′，∈）。如果可以做到这点，我们不妨就以（M′，∈）取代（M，E），因而不妨将其记作（M，∈）。此时，对任意M中的对象a∈M，M把a作为集合理解为aM={x∈M|（M，∈）x∈a}={x∈M|x∈a}=a∩M。^[25]例如，M认为第二个不可数基数所含的元素组成的集合就是（）M=∩M。但这里仍有问题，对象a∈M，但M把a理解成的aM却可能并不是M中的对象。

进一步，如果我们假设M是传递的（transitive），即

那么，上述aM=a∩M=a。由此，M中的对象ωM，当被M理解为集合时就是它们自身。这样就大大简化了考虑玩具模型时的术语，降低了由于不慎而出错的可能，也大大方便读者的理解。特别地，对集合论的传递模型而言，大量集合论术语（公式）是绝对的。

定义　3.14（绝对性）　我们称一个集合论公式对一个集合论模型（M，∈）是绝对的（absolute），当且仅当

其中，是在M下的相对化（参见第105页）。注意，相对化和绝对性的定义对集合模型和类模型都有效。可以证明，对ZF的传递模型来说，下述常见集合论术语（的定义公式）是绝对的：

（1）x是传递的；

（2）x是序数；

(3) x=ω；

(4) x=Lα；

(5) x∈L。

这些绝对性也大大方便了对传递的玩具模型性质的讨论。

不绝对的性质

需要注意的是，还有一些集合论术语往往不是绝对的。比较常见的需要谨慎处理的有：

（1）α是基数；

(2) y=P(x)。

一个集合论性质是绝对的往往是由于它是一个局部的性质。例如，传递性是绝对的是因为：要判断一个集合x∈M是否是传递的，只需要看那些x的元素和x元素的元素是否满足一些性质就可以了。而如果M本身是传递的，需要考虑的那些对象都在M里了。因此就不会出现下面这种情况：存在见证x不是传递的对象，而这些对象不在M中，所以M仍然错以为x是传递的。所以，所谓“局部的性质”是相对于模型的封闭性而言的。我们说一个性质φ（x）是局部的，是指判断x是否具有φ性质只需要依凭与x非常接近的一些集合。所谓“y与x接近”就是指根据模型M的某些封闭性，如果x∈M，那么也有y∈M。

而判断一个序数α（序数概念往往是绝对的）是否是基数，需要考虑是否存在一个满射函数f：β→α。常见的模型封闭性（传递的、满足ZF）并不能保证如果有这样的函数，那么这个函数可以从α构造出来，从而属于该模型。所以，见证α不是基数的函数，如果存在的话也未必是与α“接近的”，因此才会出现所谓的斯寇伦悖论。一个ZF的可数传递模型M才有可能将一些可数的序数错认为是ℵ1，ℵ2，...。

幂集公理是选择公理外另一个争议较大的集合论公理。如果x是无穷集合，那么P（x）中到底有哪些集合？人们可能会回答，P（x）中就是那些x的子集。但在下述意义上，我们其实并不清楚P（x）中有哪些集合：即使我们可以枚举x（把x排成良序），我们往往并不知道如何枚举P（x），后者可以被良序化恰恰需要借助具有争议的选择公理；即使P（x）能够被枚举，其基数也大于max{card x，ℵ0}，这意味着P（x）中必然存在不可构造（定义）的对象。因此，P（x）虽然可以由x通过一次集合论运算而来，但在上述直观下，它与x并不接近。事实上，P（x）与x非常遥远，以至于如果集合论幂运算是绝对的，那么绝大部分常见的集合论性质都是绝对的了。

图3.3　斯寇伦悖论

引理　3.15　令M是ZFC的传递模型。假设幂运算P（x）对M绝对，那么M=Vα或M=V。且如果是前一种情况，即M=Vα的话，那么α是一个世界基数（worldly cardinal）。^[26]进一步，如果公式并非对M绝对，那么存在集合ā，使得

换句话说，任何对这样的模型仍然不绝对的性质都蕴涵着某种大基数性质。

所以，假设M是ZFC的可数传递模型，那么我们面临的情况大致如图3.3所示。其中，M中只含有可数多个ω的子集（虽然M自认为并非可数），是一个可数序数，却被M认为是第二个不可数基数。在M外面，有着不可数多的ω的子集。因此，似乎只需要将部分M外的ω的子集排成一个长的序列g放到M中，再根据封闭性要求补充上那些又由g能构造出来的集合就可以得到一个M的扩张，记作M[g]。特别地，根据对绝对性的直观，人们有理由期待这些被放进去的ω的子集仍然会被新的模型识别为ω的子集。这样，在模型M[g]中，就有超过那么多的自然数子集了。似乎，M[g]就是我们希望构造的¬CH（即2ℵ0≥ℵ2）的模型。

但是，这样的构造可能产生一个问题。我们知道，实际上是一个可数序数，也即存在一个满射f：ω→。f本身是一个可数的集合，可以被编码为一个自然数的子集。如果我们不幸将这个自然数子集放入M[g]中了，那么在M[g]中，就可以看到一个见证是可数的函数，即不再是Mg中的第二个不可数基数，而只是一个可数序数。因此，在M[g]看来，我们也只放进去可数多个自然数的子集，也就未能保证¬CH成立。因此，我们需要更细致的构造来精确控制添加进M中的集合。接下来，将是力迫法构造的精髓。

定义　3.16（有穷部分函数集）　对集合I，J定义：

Fn（I，J）=df{p⊂I ×J|p是一个有穷函数∧dom p⊂I ∧ran p⊂J}。

定义Fn（I，J）上的（典范）偏序如下：对p，q∈Fn（I，J），

p≤q当且仅当p ⊃q。(www.daowen.com)

在力迫法的语境中，我们称偏序Fn（I，J）中的元素是条件；当p≤q时，称条件p比q强。偏序结构（Fn（I，J），≤）往往被简称为偏序Fn（I，J）。显然，偏序Fn（I，J）上有一个最大元，即Ø。在力迫法的语境中又被记作1，表示最弱的条件。我们称两个条件p，q是兼容的（记作pq），当且仅当p，q有共同的扩张r≤p且r≤q；反之，我们称p和q不兼容，记作p⊥q。在Fn（I，J）这个偏序下，pq当且仅当这两个有穷部分函数在定义域的重叠部分取了相同的函数值，即

∀x∈dom p∩dom q [p(x)=q(x)]。

利用有穷部分函数的集及函数扩张序的力迫又称作科恩力迫（Cohen forcing）。

定义　3.17（滤子）　给定一个偏序（P，≤）。我们称F⊂P是P上的滤子（filter），当且仅当它满足：

(1) 1∈F；

(2) ∀p,q∈F∃r∈F(r≤p ∧r≤q)；

(3) ∀p∈F∀q∈P(p≤q→q∈F)。

直观上，我们可以将一个偏序上的滤子理解为划出了一组被确认为成立的条件。最弱的条件总是成立；而如果两个条件p，q成立，那么总有一个似乎在说“p且q”的更强的条件成立；如果一个条件成立，那么所有比它弱的条件也成立。注意，滤子中的条件总是两两兼容的。特别地，如果F是Fn（I，J）上的滤子，那么∪F是从I到J的部分函数。

定义偏序P上的滤子U是极大的，当且仅当不存在P上的滤子H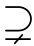U，也即对任意p∈P\U，q∈U都有p⊥q。借助选择公理可以证明，偏序上的极大滤子总存在。仍然考虑P=Fn（I，J）。容易证明，如果U是极大的话，那么∪U是一个从I到J的全函数。一个极大的滤子所包含的信息似乎是将其中所含所有条件的信息“拼接”起来（这些信息相互兼容）而得到的一个“信息完全的条件”。

现在，令I=ℵ2×ω，J=2={0，1}，U是Fn（ℵ2×ω，2）上的极大滤子，f=∪U，则f：ℵ2×ω→2是一个全函数。再对每个α＜ℵ2定义fα：ω→2，使得fα（n）=f（α，n）。这样，每个fα都是一个自然数子集的特征函数，而f就编码了一个ℵ2长的自然数子集的序列。这岂不是说明连续统的基数≥ℵ2吗？而这是ZFC中可证的。我们甚至可以把这里的ℵ2换成任意一个ℵξ。这里的问题是：极大滤子是通过选择公理得到的。我们并不清楚f到底是什么样的。特别地，我们无法确认那些fα是否两两不相等，因而无法就此认定¬CH。事实上，根据连续统假设的相对一致性，我们并不期待能直接证明在ZFC的模型中存在不少于ℵ2个两两不等的自然数子集。而力迫法通过引入一种被称作脱殊（generic）不存在于原模型（ground model）M中的对象来达到目的。

定义　3.18（稠密集）　令P是偏序。定义集合D⊂P是P上的稠密集，当且仅当对任意p∈P，存在比p强的条件q≤p且q∈D。

偏序P的一个子集代表具有某种性质的一类条件。如果这种性质的外延是一个稠密集，似乎就意味着，在我们通过拼接诸条件迈向信息完备的过程中总是无法彻底避免携带该性质的可能性。在实践中，一个稠密集往往被定义为携带某种局部或特殊性质的所有条件所组成的集合。而一系列稠密集的存在会导致无法避免这些稠密集的“信息完备的条件”满足一整套脱殊性质。

以原模型M中的偏序Fn（×ω，2）为例，我们可以对任意序数α∈、任意自然数n∈ω定义

对任意序数α，β∈定义

如果一个Fn（×ω，2）上的滤子G与上述所有稠密集相交，那么g=∪G就是一个以ℵ2×ω为定义域的函数。因为，对任意（α，n）∈×ω，存在p∈G∩Dα，n，由此（α，n）∈p⊂g。类似地，如果如上文定义gα（n）=g（α，n），则α/=β蕴涵gα/=gβ。

接下来的问题是：是否能找到这样一种脱殊的G与上述所有这些稠密集相交？容易证明，在Fn（I，J）这样的偏序上，任何一个滤子F都不能与所有的稠密集相交，因为Fn（I，J）\F就是一个稠密集。事实上，我们也并不需要与所有的稠密集相交。

定义　3.19（脱殊滤子）　令P是ZFC可数传递模型M中的偏序。我们称集合G是M上的P脱殊滤子，当且仅当G是P上的滤子，且对任意P上的稠密集D，若D∈M，则G∩D /=Ø。

也就是说，在力迫法中，我们总是只考虑原模型中的稠密集。只要与这些稠密集相交，就足够脱殊了。特别地，上面定义的偏序Fn（×ω，2）上的稠密集Dα，n和Eα，β都属于M。而由于M本身是可数的，M中的Fn（×ω，2）上的稠密集自然也是可数的。与可数个稠密集都相交的脱殊滤子G是平凡地存在的。并且，根据之前的分析，这种脱殊的对象并不存在于M中，对M来说是新的。由此，我们就成功地找到了一个长的两两不等的自然数子集序列。接下来只需要令M[G]为包含M和编码了那个序列的{G}的最小的ZFC的可数传递模型就行了。

但为了说明新的模型M[G]中就是，我们还需要更仔细地分析M[G]的构造。用比喻的方式来说就是：在M中的人们可以设计一套名称用以指称他们想象的集合。但是他们缺乏一些关键信息，以至于这些名称的所指并不清楚。而只需要补上这个关键信息，即那个可能不存在于M中的脱殊滤子，那些名称就有了明确的所指。可以证明，M[G]就是这些名称在G下指称的对象组成的集合。我们称M[G]为M的脱殊扩张（generic extension）。

所指未定的力迫名称及其所指

定义　3.20　给定偏序P。递归定义τ是一个P-名称（Pname，记作τ∈VP），当且仅当τ是一个二元关系，且对任意（σ，p）∈τ，σ是一个P-名称，p∈P。

这里，（σ，p）∈τ直观上提供了下述信息：σ这个P-名称所指称的对象（虽然M中的人们可能并不知道是什么）属于τ所指称的集合的条件或“可能性”是p。

假设M是ZFC的可数传递模型，偏序P∈M。由于P-名称对于M是绝对的，M中的P-名称MP=VP∩M。再给定M上的P脱殊滤子G，我们就可以确定每个M中的P-名称的所指。

定义　3.21　在上述假设下，对任意τ∈MP递归定义

也就是说，σ的所指σG到底属于不属于τ指称的τG看的是：是否存在可以迫使前者属于后者的条件p属于脱殊滤子G。在M中的人们虽然不知道G，但随着条件p的加强，人们会越来越清楚如果那个携带完备信息的G包含p就必须是怎样。这也就是“力迫”的直观来源。

例如，令τ={（σ1，p1），（σ2，p2），（σ3，p3）}且p2，p3≤p1，而p2⊥p3。假设我们知道p1∈G（我们并不需要G的全部信息），我们就断定σ1的所指∈τG，无论G还携带什么别的可能的信息。但我们尚不确定与是否属于τG。而当我们知道p2∈G时（此时我们仍无需知道G的全部信息），我们就可以确定∈τG，而/∈τG（G再也不可能经过p3了），除非等于或。

最后，定义脱殊扩张M[G]={τG|τ∈MP}。可以证明：

引理　3.22　在上述假设下：（1）M⊂M[G]，G∈M[G]，M[G]是ZFC的可数传递模型；

（2）对任意满足条件（1）的模型N，M[G]⊂N。

也就是说，M[G]的确是最小的包含M和G且满足那些封闭性要求的模型。

在M中的人虽然往往看不到M[G]的全貌，却可以设想：“如果G满足条件p（即p∈G），那么M[G]会是怎样的。”并且随着条件p越来越强，这种设想会越来越准确，越来越多的命题可以被断定在M[G]中成立或不成立。或者说，p迫使某些命题在M[G]中成立。反过来，如果某个命题确实在M[G]中成立，那么总有某个p迫使其成立。

再次考虑偏序Fn（×ω，2）。假设α是M中的序数，κ是M中的正则基数（regular cardinal），且α＜κ。由绝对性，α，κ也是M[G]中的序数，但κ未必是M[G]中的基数。有可能在M[G]中有一个从α＜κ到κ上的满射f，但这样的话，就有一个˙f∈MP以及一个p∈P使得M中的人相信，˙f指称了一个从α到κ的函数。显然，p也迫使人们相信˙f所指的函数的每个函数值f（ξ）都是某个＜κ的序数。只是在仅有p中信息时，M中的人们尚无法确定每个f（ξ）的值。但是M中聪明的居民可以断定每个f（ξ）至多有可数个可能的＜κ的值。因为，不同的值要有不兼容的条件迫使其实现，两个相互兼容的条件不可能迫使f（ξ）既是0又是1。另一方面，在Fn（×ω，2）中不可能存在不可数个两两不兼容的条件。因此，我们可以令F（ξ）表示所有可数个f（ξ）的可能的值。注意F是即使在M中的人们也能明确看到的函数。令X=∪ξ＜αF（ξ）。同样，X∈M，且在M中容易验证，X的序型＜κ而X又在κ中无解。这就与κ是M中的正则基数矛盾了。因此，M中的每一个正则基数（从而所有基数）都仍然是M[G]中的基数。在M中的每一个ℵξ在M[G]中仍然是ℵξ。^[27]特别地，。所以我们最终确定在M[G]中2ℵ0≥ℵ2。

回顾目前为止的构造，我们假设M是ZFC的可数传递模型，并在其中添加了必要的集合，使M[G]成为M的脱殊扩张，满足ZFC和¬CH。然而，我们希望证明的是Con（ZFC）→Con（ZFC+¬CH），即假设存在ZFC的模型，证明存在（ZFC+¬CH）的模型。在上述证明中，我们实际假设存在ZFC的传递的模型，这个假设比Con（ZFC）要强得多。它甚至蕴涵Con（ZFC+Con（ZFC）），Con（ZFC+Con（ZFC+Con（ZFC））），等等。

ZFC的可数传递的模型

假设M是ZFC的可数传递的模型。ω∈M是绝对的。在V中，我们看到M是ZFC的模型，因此Con（ZFC）成立。然而，Con（ZFC）仅仅是一个算术句子，其成立与否取决于是否有自然数编码了ZFC到矛盾式的证明。而全部的自然数已经在M中了，因此Con（ZFC）对M是绝对的。也因此，实际上M是（ZFC+Con（ZFC））的模型，也就是说，Con（ZFC+Con（ZFC））成立。再一次，Con（ZFC+Con（ZFC））对M是绝对的，因而M又是ZFC+Con（ZFC）+Con（ZFC+Con（ZFC））的模型。

更严格地，可以对α＜递归定义：

(1) T0=ZFC；

(2) Tξ+1=Tξ+Con(Tξ)；

（3）Tα=∪ξ＜αTξ（若α是极限序数）。

这里，是第一个非递归的（其序型不是一个递归关系）序数。之所以停在，是因为我们一般考虑的公理系统至少是递归可枚举的。

可以归纳地证明：如果存在ZFC的可数传递的模型，那么对每个α＜，Con（Tα）成立。

但另一方面，要证明Con（ZFC）→Con（ZFC+¬CH），只需要证明：如果（ZFC+¬CH）不一致，那么ZFC也不一致就行了。这样，只需要假设存在（ZFC+¬CH）的一个有穷部分不一致，然后找到ZFC的一个有穷部分不一致就行了。实际上，上面的证明可以作如下解读：任给（ZFC+¬CH）的一个有穷部分Λ0，我们都可以找到一个ZFC的足够丰富的有穷部分π（Λ0）。在ZFC中可以证明存在π（Λ0）的可数传递模型M，并且可以证明按照前文中叙述构造的M[G]就是Λ0的可数传递模型。但如果Λ0矛盾，那么M[G]就不可能是它的模型，因而M也不可能是π（Λ0）的模型，这就矛盾了。

下一子节，笔者将介绍另一种对力迫法证明的解读，并说明Con（ZFC）→Con（ZFC+¬CH）实际上是在一个有穷主义算术系统，如中可证的。