据唐尼（Downey，Rodney Graham）报道（Downey，2006），关于随机序列最早的刻画尝试来自于统计学家冯·米泽斯（von Mises，Richard）^[17]的（von Mises，1919）。他试图将无穷序列的随机性定义为能够通过所有统计学上的测试，例如，0和1出现的概率趋向于相等。但在对可计算性概念的刻画出现之前，他无法严格地表达“所有……的测试”。马丁-洛夫（Martin-Löf，Per）在（Martin-Löf，1966）中对随机性的定义被认为是冯·米泽斯想法的一种实现，他刻画了一种“能行测试”的概念——马丁-洛夫测试（Martin-Löf test），并定义随机序列为通过所有这种能行测试的序列。马丁-洛夫随机性（Martin-Löf randomness）得到了较广泛的接受，也是理论研究中最受关注的随机性概念。

定义　2.16（马丁-洛夫随机性）

（1）令{Gn}n＜ω是一系列统一地递归可枚举的集合族，若对任意n有勒贝格测度（Lebesgue measure）μ（Gn）≤2-n，则称{Gn}n＜ω是一个马丁-洛夫测试；

（2）称序列f∈2ω通过马丁-洛夫测试{Gn}n＜ω，当且仅当f/∈∩n＜ωGn；

（3）定义f∈2ω是马丁-洛夫随机的，当且仅当f通过所有马丁-洛夫测试。

其中，称{Gn}n＜ω是一系列统一地递归可枚举的集合族，当且仅当{^[18]是递归可枚举的，也即的（见第59页）。一个马丁-洛夫测试可以被直观地理解为一则可以能行地得到的排他性质。一般用测度为0来刻画排他性。随机的序列被认为无法被任何一种独特的排他性质挑选出来。例如，对任意递归函数f∈2ω，令，则是一个马丁-洛夫测试，并且因此，所有递归的01序列都不是马丁-洛夫随机的。事实上，上述可以对任意序列f∈2ω定义，这样任何无穷01序列f都具有排他性质，即因此，必须将我们考虑的排他性质限制为某种能行性的随机性测试，否则所有序列都不是随机的了。

在同一篇文章中，马丁-洛夫通过能行地枚举所有统一递归可枚举集合族构造了一个通用马丁-洛夫测试{Un}n＜ω，使得一个序列是马丁-洛夫随机的，当且仅当它可以通过这个通用马丁-洛夫测试。由于未通过通用马丁-洛夫测试的实数只有勒贝格测度0那么多，因此马丁-洛夫随机的实数类是勒贝格测度1的。

另一方面柴廷（Chaitin，1975）将K-随机概念推广到无穷01序列，获得了基于不可压缩性直观的随机性概念，即序列f∈2ω是随机的，当且仅当它的所有真前段不可压缩。施诺尔（Schnorr，Claus-Peter）在（Schnorr，1973）中证明了这两种定义是等价的。

定理　2.17（施诺尔）对01序列f∈2ω，以下等价：

（1）f是马丁-洛夫随机的；

（2）存在常数c，对任意n＜ω有K（f↾n）＞n-c。

事实上，对任意常数c，令是在c下K-随机的}，则{Rc}c＜ω是一个通用马丁-洛夫测试。

不可预测性可能是人们对随机性最直观的理解，例如赌局中骰子每次掷出的是大点还是小点。基于不可预测性对随机性概念的刻画来自概率论学家。保罗·莱维（Lévy，Paul Pierre）在（Lévy，1937）中给出了一种押注策略的形式化。

定义　2.18（马提克策略）　令d：2＜ω→R≥0是一个以01字符串为定义域，以≥0的实数为值域的函数。

（1）我们称d是一个马提克策略（martingale），当且仅当对任意σ∈2＜ω，

（2）我们称d是一个超级马提克策略（supermartingale），当且仅当对任意σ∈2＜ω，

（3）我们称一个（超级）马提克策略d在序列f∈2ω上获胜，当且仅当

考虑押注骰子大小或硬币正反的系列赌局，庄家有无穷多的筹码。玩家每轮可以部分押大部分押小，押对的部分获得双倍收益，押错的部分则全部损失。玩家根据马提克策略d押注，初始筹码数量为d（Ø），在第一轮中拿d（0）/2押小，拿d（1）/2押大。假设我们预先知道骰子每次掷出的大小会排列成序列f∈2ω，那么，第一轮过后，玩家拥有的筹码就是d（f（0））。第二轮，玩家按照d拿d（f（0）0）/2押小，拿d（f（0）1）/2押大，结果拥有筹码d（f（0）f（1））。依此类推。一个马提克策略能在一系列赌局f∈2ω上最终获胜，当且仅当根据这个策略能获得任意高的回报。换句话说，玩家可以任意设定预期回报，并按照马提克策略押注，直到达到预期回报。超级马提克策略是对马提克策略的推广，玩家在每轮未必要用他所有的筹码下注，可以拿出一部分来消费。人们关于赌局不可预测的直观可以被表示为：没有马提克策略能够在随机序列f∈2ω上获胜。

当然，如果已经预先知道f∈2ω，定义马提克策略d使得每次都按照f押注，d自然能在f上获胜。因此，为了刻画不可预测性，仍然必须对马提克策略做能行性方面的限制。

实数值函数的能行性

我们之前定义的递归函数或递归可枚举函数都是针对自然数上的函数。对于可数实数值函数d：2＜ω→R，可以定义：

（1）可数实数值函数d是（统一地）递归的，当且仅当集合

是递归的；

（2）可数实数值函数d是（统一地）递归可枚举的，当且仅当上述集合是递归可枚举的。

直观上，一个可数实数值函数d是递归可枚举的，那么我就有一个统一的能行方法从小到大逼近它的每个取值d（σ），但在任意时刻我们并不能确定它的值最终会有多大。而如果d又是递归的，就存在统一的能行方法从大小两个方向逼近它的每个函数值。

施诺尔在（Schnorr，1971）中定义了能行化的马提克策略概念，并用它来刻画随机性。他证明：马丁-洛夫随机等价于某类能行马提克策略的失效。

定理　2.19（施诺尔）序列f∈2ω是马丁-洛夫随机的，当且仅当不存在递归可枚举的（超级）马提克策略能在f上获胜。

由此，人们分别从无法用排他性质刻画、不可压缩性与不可预测性三个不同的角度试图刻画随机性，却得到了等价的定义。这里的情形似乎与人们试图能行过程时的情况（见1.1.5节）类似。人们从不同的角度出发对同一个概念得到了等价的刻画这一事实构成了一组经验证据，让人们相信这些定义的确成功地刻画了有关概念。然而，马丁-洛夫随机对随机性概念的刻画远没有像图灵机对能行过程的刻画那样获得几乎一致的认同。

施诺尔（Schnorr，1971）就认为，马丁-洛夫测试并不是一种可以能行地得到零测度实数集的过程，而另一方面，递归可枚举的马提克策略也无法刻画能行的马提克策略概念。为此，他提议了另两种随机性概念，一个是施诺尔随机（Schnorr randomness），一个是可计算随机（computable randomness）。

定义　2.20（施诺尔随机性）

（1）一个马丁-洛夫测试{Gn}n＜ω是一个施诺尔测试（Schnorr test），当且仅当每个Gn的勒贝格测度μ（Gn）是统一地递归的；

（2）称序列f∈2ω通过施诺尔测试{Gn}n＜ω，当且仅当f∈/∩n＜ωGn；

（3）定义f∈2ω是施诺尔随机的，当且仅当f通过所有施诺尔测试。

相比马丁-洛夫随机性的定义，施诺尔测试的定义更严格，它要求每个Gn的测度是几乎确定的。可以证明，就基于其上的随机性概念而言，施诺尔测试可以等价地定义为要求每个μ（Gn）=2-n。要求每个测度μ（Gn）统一地可计算的意义在于：在统一能行地生成测试{Gn}n＜ω的过程中，对马丁-洛夫测试而言，人们也不知道什么时候生成结束（即使某个Gn的生成已经完成了），而对施诺尔测试而言，如果Gn的生成完成了，即达到了预定的测度，那人们就知道已经完成了。因此，施诺尔测试似乎更符合能行的直观。更严格的测试概念意味着更少的测试，也意味着施诺尔随机是相比马丁-洛夫随机更弱的概念。(www.daowen.com)

另一方面，施诺尔认为，递归可枚举的（超级）马提克策略也与能行的直观不符。而递归的马提克策略是更自然的对能行策略的刻画。

定义　2.21（可计算随机）　序列f∈2ω是可计算随机的，当且仅当没有递归的马提克策略可以在其上获胜。

由于递归的马提克策略也是递归可枚举的马提克策略，可计算随机也是比马丁-洛夫随机更弱的随机性概念。这些较弱的随机性概念同样拥有来自其他角度的等价刻画。例如，施诺尔随机有基于柯尔莫哥洛夫复杂度的刻画，也有基于马提克策略的比可计算随机更严格的刻画。因此，施诺尔随机是比可计算随机更弱的随机性概念，即：

马丁-洛夫随机⇒可计算随机⇒施诺尔随机。

施诺尔随机的等价刻画

施诺尔认为，可计算随机背后的马提克策略仍然不够能行。如果一个递归的马提克策略可以在一个非可计算随机序列上获胜，那么玩家按照这个马提克策略押注可以获得任意高的预期回报。但是，他可能并不知道需要多久才能达到他的预期回报。为此，可以用自然数上的非降函数h：N→N来表示随着时间（轮数）而增长的预期回报。我们总是贪心地希望不仅马提克策略d能在序列f上获胜，而且存在一个能行的方法来预测我们的收益，即存在递归的非降函数h：N→N使得

施诺尔证明（Schnorr，1971）：序列f∈2ω不是施诺尔随机就意味着存在一个能行的马提克策略也存在一个能行的回报预期，使得玩家按照这个马提克策略押注，在序列f上几乎总是可以获得超过预期的回报。

定理　2.22（施诺尔）序列f∈2ω是施诺尔随机，当且仅当对任意递归的马提克策略d以及任意递归的非降函数h：N→N，（2.6）都不成立。

由于对于获胜还额外要求能行的回报预期，施诺尔随机比可计算随机更弱。

唐尼和格里菲思（Griffiths，Evan J.）在（Downey and Griffiths，2004）中得到了对施诺尔随机基于不可压缩性的等价刻画。定义一个无前束程序M是一个递归测度程序，当且仅当它“停机的概率”（见第87页）是递归的。

定理　2.23（唐尼-格里菲思）序列f∈2ω是施诺尔随机，当且仅当对任意递归测度程序M都存在常数c使得KM（f↾n）≥n-c。

另一方面，也有人认为马丁-洛夫随机性太弱了。称一个实数或一个无穷01序列f∈2ω是左递归可枚举的（left recursively enumerable），当且仅当位于它“左侧”的有穷字符串是递归可枚举的，即集合是递归可枚举的。^[19]直观上，如果一个实数（或01序列）是左递归可枚举的，那么就存在能行的方法从小到大（或从左到右）逼近它。能够被这样能行地逼近的序列似乎不能被认为是随机的，然而，可以证明存在左递归可枚举的马丁-洛夫随机序列。

对每个无前束程序M，可以定义它的停机概率

每个无前束程序的停机概率都是一个[0，1]中的实数。令Upf是通用无前束程序，则柴廷停机概率（Chaitin’s halting probability）Ω被定义为Upf的停机概率。

柴廷证明（Chaitin，1975）：Ω是马丁-洛夫随机的。Ω不仅具有一定的能行性质，它也可以作为神谕提供许多信息。事实上，Ω与停机问题图灵等价，Ω≡TØ′。更进一步的研究表明，马丁-洛夫随机序列作为神谕可以是任意有力的：对任意集合A，存在马丁-洛夫随机集合B使得A≤TB。携带大量有用信息的随机序列似乎也与人们的直观不符。在上述意义上，马丁-洛夫随机性概念确实显得过于宽泛了。

一种自然的加强马丁-洛夫随机性概念的方式是放宽对马丁-洛夫测试能行性的要求。例如，我们可以利用神谕X，只要求每个测试是统一地在X中递归可枚举的就可以了。由此，定义序列f∈2ω是相对于X马丁-洛夫随机的，当且仅当它可以通过所有在X中递归可枚举的测试。类似地，在基于不可压缩性的定义中，可以允许无前束程序以X为神谕；在基于不可预测性的定义中，允许马提克策略在X下递归可枚举。可以证明，这三种“相对神谕的随机性”是等价的。

定理　2.24　给定序列f∈2ω、集合X⊂N，以下命题等价：

（1）f是相对于X马丁-洛夫随机的；

（2）存在常数c，对任意n＜ω有KX（f↾n）＞n-c；

（3）不存在X下递归可枚举的（超级）马提克策略能在f上获胜。

马丁-洛夫随机的相对化中又有一类是典范的，即相对于Ø′（停机问题）、Ø′′乃至任意Ø（n）的随机性概念。

定义　2.25（n-随机）　令n≥1。称序列f∈2ω是n-随机的（nrandom），当且仅当f是相对于Ø（n-1）马丁-洛夫随机的。

另一方面，每个马丁-洛夫测试是一个类，我们将其放宽为类就得到一系列随机性概念。考茨（Kautz，Steven M.）证明（Kautz，1991）：随机与n-随机等价。由此，可以进一步推广，定义序列f是算术随机的（arithmetically random），当且仅当对任意n＜ω，f是n-随机的。

2-随机（即相对于Ø′的马丁-洛夫随机）已经修复了一些马丁-洛夫随机性概念与直观不符的性质。例如，所有在Ø′中递归的序列都不是2-随机的。特别地，Ω不是2-随机的。此外，2-随机集合不会像一些马丁-洛夫随机集合一样，当2-随机集合作为神谕的时候并不能提供“有用的”信息。作为定理2.28的推论，2-随机集合无法计算停机问题Ø′。因此，无论在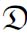T（≤T0′）还是在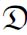T（≥T0′）中，都没有2-随机的集合。

2-随机也有基于不可压缩性的自然刻画，并且这种刻画不依赖于对柯尔莫哥洛夫复杂度或无前束柯尔莫哥洛夫复杂度的相对化。尼茨（Nies，André）、斯蒂芬（Stephan，Frank）和特尔文扬（Terwijn，Sebastiaan A.）在（Nies et al.，2005）中证明了：序列f∈2ω是2-随机的，当且仅当它有无穷多个C-随机的前段。由于强K-随机蕴涵C-随机，所以有无穷多个强K-随机前段的序列也都是2-随机的。米勒（Miller，Joseph S.）在（Miller，2009）中证明：2-随机序列有无穷个前段是强K-随机的。

定理　2.26（米勒-尼茨-斯蒂芬-特尔文扬）给定序列f∈2ω，下述命题等价：

（1）f是2-随机的；

（2）存在无穷多个f的前段是C-随机的；

（3）存在无穷多个f的前段是强K-随机的。

除了通过降低对马丁-洛夫测试本身能行性的要求来获得强的随机性概念，还可以通过降低对马丁-洛夫测试趋向于零测集过程的能行性的要求来加强随机性概念。令{Gn}n＜ω是一系列统一地递归可枚举集合族，称{Gn}n＜ω是一个广义马丁-洛夫测试，只要求它们的测度趋向于0，即limn＜ωμ（Gn）=0就可以了。称序列f∈2ω是弱2-随机的（weakly 2-random），当且仅当它能通过所有广义马丁-洛夫测试。读者可以对比施诺尔随机性的定义，其中施诺尔加强了对趋向于零测过程的能行性要求。可以证明，弱2-随机性的强度严格介于马丁-洛夫随机性和2-随机性之间。

当然，我们还可以进一步放宽条件允许更强的测试，譬如的零测集、的零测集……这样，我们就有：

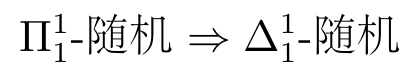⇒2-随机⇒弱2-随机⇒马丁-洛夫随机。

迄今为止，大部分的随机性概念都按强弱排列成线序。^[20]也许，正确的随机性概念就是其中的一个，但更多的迹象表明，没有一个随机性概念可以完美地诠释人们关于随机性的各种直观。这些随机性概念在内在性辩护（intrinsic justification）方面都有各自的优势。它们也往往具有不同的等价定义，并且都有与可计算性等其他领域概念的良好互动，因而都能获得相当程度的外在性辩护（extrinsic justification）。或许，就人们对于随机性的直观本就不可能像对可计算性那样有一个典范的刻画，各种随机性概念从弱到强排列而成的层谱结构或许才是正确的结果。如果更多的随机性概念被发现且都很好地按照强弱排列为一个线序，那么层谱论会得到更多的支持；而如果出现越来越多不可比的随机性概念，那么情况会变得更加扑朔迷离。无论如何，现代逻辑学家的工作——试图用严格的语言刻画随机性概念，通过演绎证明这些刻画之间以及它们与其他基础概念之间的联系——切切实实地推动了人们对随机性的理解。