在有意义地谈论随机性概念之前，首先需要明确随机是关于什么的性质。物理学家会说，单个光子偏正的方向是随机的。“单个光子偏正的方向”在这里指什么？将单个光子射入特定角度的偏正镜并测量该光子是否能够穿过偏正镜，可以粗略地测量入射光子的偏正方向。这时“单个光子偏正的方向”被分为两类，即通过与不通过，或记作{0，1}。我们当然不能称0或1是随机的。更精确地，物理学家的意思是不存在什么物理规律能够根据固定的已知的情况预测某个单子的偏正方向。正如所谓预言家总有正确的时候，所谓无法预测肯定不是指某个个案无法被猜到，而是指不存在什么方法可以一次又一次地猜对，或者说在对一系列偏正方向{0，1}的预测中获得超过一半的正确率。因此，所谓无法被预测的或者随机的是一系列光子的偏正方向序列。在经验科学的意义上，只需要足够长的序列就可以构成判断随机性的经验证据；而在更严格的数学意义上则要求无穷长的序列（有穷次和单次并没什么区别）。

再如，在热力学和信息学中，熵被用来刻画一个封闭的热力学系统或一个信息源的随机程度。现代信息学的核心概念香农熵（Shannon entropy）被定义为

其中，是一组[0，1）中的实数。S被直观地理解为一个信息源，其中每个pi表示该信息源输出可能变量ai的概率。例如，一个信息源以平均的概率（pi=1/256）输出ASCII码字符，那么它的熵是8。根据（Shannon，1948）中的信息源编码定理（source coding theorem），随着m趋向于无穷，无损压缩信息源m次输出所需的比特（01字符）数是m与香农熵的积m·8。显然，信息源的熵越高，它输出的信息越难以被压缩（需要被编码为更多比特）。在这层意义上，更高的熵似乎的确意味着更随机。给定n，令当每个pi=1/n时H（S）取最大值。显然，我们没有理由认为S=〈1/2，1/2〉是某种拥有最大随机性的对象。而下述说法则显得更符合直观：以〈1/2，1/2〉概率输出0或1的生成的01序列比以〈1/3，2/3〉概率输出0或1生成的01序列更随机。

因此，当人们抽象地谈论随机性概念时，它应该被视作关于一组独立事件或符号的无穷序列的性质。不失一般地，可以认为随机性是关于无穷01序列的性质，也即等价于是关于自然数集（的特征函数）或[0，1]间实数（的二进制表达）的性质，而这些也是递归论学家的研究对象。20世纪六七十年代以后，随机性理论逐渐成为递归论的主要研究方向也就不令人意外了。

柯尔莫哥洛夫（Kolmogorov，Andrey）在（Kolmogorov，1963）中对有穷01序列（又称01字符串）的分析是现代随机性理论的开端之一。柯尔莫哥洛夫基于对不可压缩性的描述来刻画01字符串的随机性。计算机解压缩程序往往可以将较小的文件解码为较大的源文件，我们可以将其抽象为以01字符串为输入和输出的图灵机（部分递归函数）：M：2＜ω→2＜ω。若τ可以被M解码为σ，即M（τ）=σ，则称τ是σ的一个M-描述（Mdescription）。对任意01字符串σ∈2＜ω，定义σ在解压缩程序M下的柯尔莫哥洛夫复杂度（Kolmogorov complexity）为

注意，如果不存在σ的M-描述，那么CM（σ）=∞。如果字符串σ不存在比σ本身更短的M-描述，则称σ是M不可压缩的。M不

可压缩性依赖于特定解压缩程序，无法作为对随机性的一般刻画。对再复杂的字符串，也可以设计相应的程序强行将0或1作为它的描述。为此，我们期望设计一种通用解压程序U：2＜ω→2ω可以以固定的代价来模拟任意一款解压缩程序。令{Me|e＜ω}是对所有解压缩程序（图灵机）的枚举。定义

①后文中在讨论01字符串的语境下亦将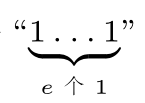记作1e。

定义通用解压缩程序U，使得对任意形如1e0τ的输入，U调用程序Me，并试图输出Me（τ）。这样，如果字符串σ有一个Me-描述，那么它在通用解压缩程序下的描述不会比它的Me-描述长超过一个常数，即

在这个意义上，U的确是足够通用的解压缩程序。因此，可以定义一个01字符串σ的柯尔莫哥洛夫复杂度为

C(σ)=CU(σ)。

容易证明，每个01字符串σ的柯尔莫哥洛夫复杂度都几乎小于等于自身的长度。即存在常数cid，使得对任意01字符串σ，有

事实上，这里的常数cid可以取某个等同映射程序=id的编码eid+1。类似地，解压缩程序Me=h也可以看作一个部分递归函数，那么C（h（σ））≤C（σ）+e+1，这也符合人们关于解压缩后的文件的复杂度不超过压缩文件复杂度的直观。

给定常数d，我们可以称所有满足C（σ）≥|σ|-d的01字符串σ都是C-随机的（C-random），这符合人们关于不可压缩性的直观，并且该定义不依赖于特定的解压缩程序，具有足够的一般性。由于长度＜n的01字符串只有2n-1个而长度为n的字符串有2n个，所以对任意n，总存在长度为n的字符串σ使得C（σ）≥n=|σ|，也即总存在C-随机的字符串。

这种对有穷01序列的随机性刻画仍然有一些弊端。首先，柯尔莫哥洛夫复杂度只有当01字符串的长度足够长以后才能忽略常数带来的影响，从而更符合直观。当然，这是在以有穷01序列为对象谈论随机性时不可避免的。并且，确实只有针对足够长的01序列谈论随机性才更有意义。柯尔莫哥洛夫复杂度的另一个弊端更加微妙，但却是可修复的。在柯尔莫哥洛夫复杂度的解释中，我们除了可以从每个01字符串σ中提取它携带的直接信息外，还可以提取关于它本身的元信息：字符串的长度|σ|。后者可以被写成log（|σ|）长的字符串，因此每个字符串σ实际上至少携带|σ|+log（|σ|）这么多字节的信息。这种“作弊”的方法可以被用来证明下述定理。

定理　2.15　对任意实数x∈2ω，对任意自然数k∈ω，存在x的前段σx，使得

C(σ)＜|σ|-k。

利用字符串长度携带额外信息的“作弊”方法

考虑这样一个解压缩程序Me：输入任意字符串ρ，该程序先算出ρ的长度|ρ|的二进制表达θ，再输出θρ。^[14]这时ρ是θρ的Me-描述。在将ρ解压缩为θρ的过程中，程序Me“作弊地”使用了ρ的长度信息，因此，CMe（θρ）=|ρ|。(www.daowen.com)

给定自然数k，取x的足够长的前段θ使得|θ|＞k+e+1。假设θ是n的二进制表达。再截取x中θ后的n位ρ，即|ρ|=n且θρx。令σ=θρ，那么

C(σ)=CMe(θρ)+e+1=|ρ|+e+1

直观上，任意两个字符串σ，τ的连接στ的复杂度（所携带的信息）应该不会超过σ与τ复杂度的和加一个常数（στ无非就是将τ连接到σ之后所得到的），即存在常数c使得但给定任意常数c，根据定理2.15，总可以找到足够长的01字符串μ使得C（μ）≥|μ|，并且可以找到它的一个前段σ，使得μ=στ并且C（σ）＜|σ|-（c+cid）。又由C（τ）≤|τ|+cid，

C(στ)=C(μ)≥|μ|=|σ|+|τ|＞C(σ)+C(τ)+c，

显然与直观（2.4）不符。

列文（Levin，Leonid）在他的博士论文（Levin，1971）中首次提议使用无前束程序（prefix-free machine）代替一般的解压缩程序。我们称一个程序（或图灵机）M是无前束程序，当且仅当它定义域中的字符串是两两不相容的，即对任意σ，τ∈2＜ω，如果M（σ）↓且M（τ）↓，那么σ和τ不是彼此的前段。对每个解压缩程序Me，可以能行地将其改造为一个无前束程序Pe：固定某个对自然数s和01字符串σ组成的有序对（σ，s）的能行排序，按照这个排序逐一计算Me，s（σ），如果Me，s（σ）↓并且不存在之前的（t，τ）使得Me，t（τ）↓并且有τσ或στ的话，输出Pe（σ）=Me，s（σ）。显然，Pe是无前束程序，并且若Me是无前束程序，则PeMe。因此，能行地枚举了所有无前束程序。由此，我们可以用与定义通用解压缩程序同样的方式（见第79页）定义通用无前束程序Upf。类似地，定义字符串σ的无前束柯尔莫哥洛夫复杂度（prefix-free Kolmogorov complexity）为

K（σ）=KUpf（σ）。^[15]

显然，利用长度信息“作弊”的方法（见第80页）不再适用于无前束柯尔莫哥洛夫复杂度，并且存在常数c，使得对任意字符串σ，τ∈2＜ω有

考虑程序Me：对任意输入μ，搜寻字符串对（θ，η）使得μ=θη并且θ，η∈dom Upf，一旦找到便输出Upf（θ）Upf（η）。容易验证，Me=Pe是无前束程序，并且μ∈dom Me当且仅当μ能被划分为两个Upf-描述的连接。由此，取c=e+1时，（2.5）成立。

显然，无前束柯尔莫哥洛夫复杂度能够解压缩的描述字符串少了很多，因而没有普通的柯尔莫哥洛夫复杂度经济：C（σ）≤K（σ），但每个01字符串σ的无前束柯尔莫哥洛夫复杂度仍然有一个可以接受的上界。考虑仅在每个形如0|σ|1σ（σ∈dom Upf）上有定义的程序Me，使得

Me(0|σ|1σ)=σ，

那么M是一个无前束柯尔莫哥洛夫复杂度，并且见证了

K(σ)≤2|σ|+e+1。

事实上可以进一步证明，存在常数c，使得对任意字符串σ有K（σ）≤|σ|+2 log（|σ|）+c。柴廷（Chaitin，Gregory）在（Chaitin，1975）中证明

K（σ）≤|σ|+K（|σ|）+c^[16]

是关于K（σ）的精确上界。

类似基于柯尔莫哥洛夫复杂度定义的C-随机性，给定常数d，我们可以定义有穷01序列σ是K-随机的（K-random），当且仅当K（σ）≥|σ|-d。由于每个无前束程序也是普通解压缩程序，因此每个C-随机的字符串也是K-随机的。反之则未必成立。基于柴廷给出的精确上界，还可以定义σ是强K-随机的（strongly K-random），当且仅当K（σ）≥|σ|+K（|σ|）-d。索罗维（Solovay，Robert Martin）在（Solovay，1975）中证明了，在恰当的常数下，强K-随机蕴涵C-随机，但存在常数c，使得对任意常数d都存在无穷多字符串，在常数c下是C-随机的但不是在常数d下强K-随机。

关于有穷字符串的复杂性理论同时也是现代信息科学的研究对象，在应用和纯理论领域都具有重要意义。当然，关于有穷字符串的随机性概念或严重受制于常数的选择，或只有当字符串长度趋向于无穷时才表现出与直观相符，因此，有穷字符串并不是随机性概念的理想载体。但是，有穷字符串的复杂性理论及有关概念被大量运用于对关于无穷01序列（或自然数集、实数）的随机性理论。