波斯特在（Post，1948）首次明确定义了现代意义上的图灵度（Turing degree）概念作为都“不可解的度”的精确刻画。由自然数集X代表的图灵度被定义为包含X的图灵等价关系下的等价类：

同一个图灵度中的集合具有同样的图灵归约概念下的计算复杂度。假设[X]T和[Y]T是图灵度，定义[X]T≤T[Y]T，当且仅当X≤TY。容易证明，这个定义是合理的，选取[X]T或[Y]T中的其他代表元素不会带来什么区别。令

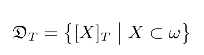
是所有图灵度组成的集合，则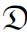（T，≤T）是一个偏序（partial order）结构^[8]，又被称作（全局）图灵度结构（global Turing degree structure）。可以说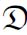，（T，≤T）就是“图灵归约”概念的外延。

（Kleene and Post，1954）开启了对图灵度结构的研究计划，他们指出了关于结构（T，≤T）的一些简单事实。由于计算机程序或带神谕的图灵机只有可数多个，所以每个图灵度的基数是可数的，因此，T的基数与连续统的基数一样，即。尽管如此，对每个图灵度x，由x的前驱组成的前段是可数的，因此，我们称结构（T，≤T）满足可数前驱性质（countable predecessor property）。

显然，T有一个最小元0=[0]T，即所有可计算集合组成的图灵度。但是T没有极大元。对每个集合X，都有一个“相对于X的停机问题”，它的复杂度严格地高于X的复杂度，被称作X复杂度的图灵跃迁（Turing jump）。

定义　2.9（图灵跃迁）　对集合X，定义X跃迁（记作X′）为相对于它的停机问题，即

对图灵度x=[X]T，定义x′=[X′]T。

容易证明，x′的定义与x中代表元素的选取无关。特别地，0′=[K]T。停机问题不可计算的证明可以统一地推广至对的证明。因此，对每个图灵度x，都有一个比它更高的图灵度x′。

接下来克莱尼和波斯特发现，在T上有一定的代数结构。对任意集合X，Y，定义它们的信息和

由此，X⊕Y的偶数部分携带了原本X的信息，而X⊕Y的奇数部分携带了Y的信息。显然，如果知道X⊕Y，就可以判定X和Y（X≤TX⊕Y且Y≤TX⊕Y）。而对任意集合Z，如果X≤TZ且Y≤TZ，那么X⊕Y≤TZ。类似地，对图灵度x=[X]T和y=[Y]T，可以定义

可以证明，x∨y是x，y在偏序≤T下的上确界，因此，T是一个向上的半格（upper semi-lattice）。

格与半格

假设（L，≤）是一个偏序，令x，y∈L。我们称u是{x，y}的上确界，当且仅当u是{x，y}的上界（即x，y≤u），并且对{x，y}的任意上界z都有u≤z。类似地，定义{x，y}的下确界为{x，y}最大的下界。例如，在自然数上的整除关系下，{n，m}的上确界、下确界分别为{n，m}的最小公倍数和最大公约数。在偏序结构中，上确界和下确界未必总是存在。如果偏序（L，≤）中任意两个元素的上确界和下确界都存在，就称（L，≤）是一个格（lattice）。而如果（L，≤）只在上确界（或下确界）下封闭，则称（L，≤）是向上的（或向下的）半格（semi-lattice）。

在格（半格）上可以定义代数运算。例如，定义x∨y为{x，y}的上确界，定义x∧y为{x，y}的下确界。可以证明，（L，∨）和（L，∧）都是满足结合律、交换律和幂等性（例如，x∧x=x）的代数结构。在满足结合律、交换律和幂等性的结构（L，∨）上可以定义偏序：

重新得到（偏序意义上的）半格。

代数结构（L，∨，∧）满足分配律，当且仅当它满足

以及

满足分配律的格又被称作分配格。

如果分配格（L，∨，∧，0，1）有最大元1和最小元0并且在补运算下封闭，即对任意x∈L，存在y∈L使得

那么L就是一个布尔代数。

半格（L，≤，∨）虽然只有一个代数运算，也可以定义分配律如下：对任意x，y，z∈L，如果z≤x∨y，那么存在x0≤x和y0≤y使得z=x0∨y0。满足上述分配律的半格被称作分配半格。可以证明，如果分配半格也在下确界下封闭，那么它就是一个分配格。

克莱尼和波斯特证明（Kleene and Post，1954，Theorem 3），存在一对没有下确界的图灵度，因此T不是一个格。克莱尼和波斯特在文章中发明了一种被称作“算术力迫法”（forcing in arithmetic，力迫法简介见3.3节）的方法，用以构造一系列不可比的图灵度。

定理　2.10（克莱尼-波斯特）　存在图灵度a1，a2，使得0＜Tai＜T0′（i=1，2）且a1与a2不相容（即a1Ta2且a2Ta1）。^[9]

一般地，对任意图灵度a及任意自然数k，存在k个彼此独立的图灵度b1，...，bk，使得a＜Tbi＜Ta′（i=1，...，k）。^[10]

克莱尼-波斯特算术力迫论证

我们试图构造一对集合A，B满足且。

对定义在自然数上的二值函数σ，τ∈2＜ω，σ⊂τ当且仅当τ是σ的尾节扩张。显然，（2＜ω，⊂）是一个偏序。令...是2＜ω上的一个无穷链，则∪i＜ωσi∈2ω是一个自然数上的二值全函数。

事实上，我们将构造2＜ω上的无穷链...和...，使得χA=∪i＜ωσi和χB=∪i＜ωτi分别是集合A和B的特征函数，并且逐一满足要求：

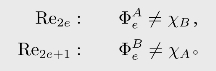
首先令σ0=τ0=0。

在第2e+1步，σ2e和τ2e已被构造，我们试图扩张它们以满足Re2e。令^[11]是第一个不在τ2e中的自然数。如果

成立，那么令σ2e+1=满足（2.2）的“最小”的ρ，而令τ2e+1=，也即把n放入τ2e+1的定义域并赋以与不同的值。由此，无论σ2e+1和τ2e+1之后如何扩张，例如，对任意χA，χB∈2ω满足χA⊃σ2e+1以及χB⊃τ2e+1，都有

而如果（2.2）不成立，那么任意扩张σ2e。例如，令σ2e+1=，令。类似地，无论σ2e+1和τ2e+1之后如何扩张，都有

所以，无论（2.2）成立与否，σ2e+1和τ2e+1的构造保证了

成立。用力迫法的术语，即（σ2e+1，τ2e+1）Re2e。类似地，可以构造。

注意，σ2e+1和τ2e+1的构造中唯一非能行的部分是对（2.2）的判断，而（2.2）是一则公式，因而可以图灵归约到停机问题，所以，由此构造出来的A，B≤TK。

需要注意的是，克莱尼-波斯特定理并没有能直接回答波斯特在（Post，1944）中提出的波斯特问题，后者要求构造的是不相容的递归可枚举的图灵度，而这里构造的仅仅是≤T0′的图灵度，并非所有在停机问题下可计算的集合都是递归可枚举的。

克莱尼-波斯特定理和其中的构造方法有力地促进了对图灵度结构的理解。作为克莱尼-波斯特定理的直接推论，可以证明任何有穷偏序都可以被嵌入T。萨克斯（Sacks，Gerald）在（Sacks，1963）推广了克莱尼-波斯特结果，证明每个可数的偏序都可以被嵌入T，甚至每个满足可数前驱性质的基数≤ℵ1的偏序都可以被嵌入T。萨克斯猜想，每个满足可数前驱性质且基数≤2ℵ0的偏序都可以被嵌入T。如果连续统假设成立，萨克斯的猜想自然成立，但这在ZFC中是否可证尚未可知。无论如何，已有的结果表明，图灵度全局结构T是一个具有相当普遍性的偏序结构。

在T中嵌入有穷偏序(www.daowen.com)

推论2.11对任意有穷偏序（n，≼），存在一一的函数h：n→T使得对任意i，j＜n，

令{ai |i＜n }是彼此独立的图灵度，定义bi=j≼iaj。容易验证，h（i）=bi满足要求（见图2.7）。

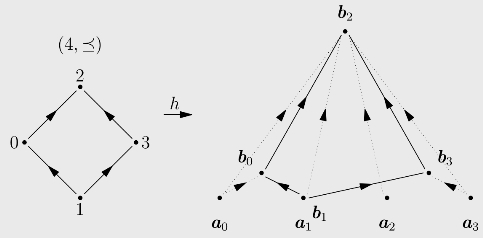
图2.7　在T中嵌入有穷偏序

斯佩克特（Spector，Clifford）在（Spector，1956）推广了（Kleene and Post，1954）中的一些结果，并回答了其中提出的若干问题。例如，他证明了T不是稠密的，并且拥有非零极小元。

定理　2.12（斯佩克特）对任意图灵度a，存在图灵度c＜Ta′′且a＜Tc，使得不存在图灵度b满足a＜Tb＜Tc。

对严格上升的无穷图灵度序列a0＜Ta1＜T...，斯佩克特构造了被称作精确对（exact pair）的一对图灵度b，c，使得对任意图灵度d，若d≤Tb且d≤Tc，则存在i＜ω使得d≤Tai。显然，精确对{b，c}没有下确界。而T中的任何无穷递增序列之上都有精确对，因而没有上确界。所以，T不是在上确界意义上ω-完全的。

（Kleene and Post，1954）开启的另一条问题线索是结构（T，≤T）中的可定义问题。图灵跃迁可能是图灵度结构上最重要的运算，许多关于图灵度的性质都需要援引图灵跃迁来定义。克莱尼和波斯特问道：图灵跃迁是否能够在偏序结构（T，≤T）中被定义？直到1990年，才由库珀（Cooper，S. Barry）声称证明了，图灵跃迁和“在……中递归可枚举”（例如，a′在a中递归可枚举）都是在（T，≤T）中可定义的（Cooper，1990）。^[12]

斯佩克特对精确对的构造可以推广至T上的可数理想（ideal）^[13]。假设I是T上可数理想，那么存在精确对b，c，使得对任意图灵度a∈T，

a∈I⇔ a≤Tb且a≤Tc。

因此，T上的所有可数理想都是以其上的精确对作为参数可定义的。

相反，要证明某些具体的性质、关系或运算在一个结构中不可定义，通常的方法是构造该结构上的一个非平凡的自同构（automorphism），并证明那些性质、关系或运算在这个自同构下不保持。而如果证明一个性质或关系在所有自同构下都保持，那么它有较大的可能是可定义的。因此，对T上自同构的研究与对T上可定义问题的研究是相辅相成的。然而，一直以来人们并没有发现T上的非平凡自同构。但是，这并不妨碍人们问：如果T存在非平凡的自同构，那么它会是怎么样的？

斯拉曼（Slaman，Theodore Allen）和武丁（Woodin，William Hugh）在（Slaman and Woodin，1986）中推广了斯佩克特的结果，给出了一种对T上任何可数关系的统一编码。

定理　2.13（斯拉曼-武丁编码定理）假设R是T上的可数关系，那么R在T中参数可定义。具体地，对任意k∈ω，存在一则公式

φ(x1,...,xk,y1,...,ym)，

使得对任意T上的可数k元关系R，存在参数（编码）p1，...，pm∈T，使得φ在T中定义R，即

斯拉曼-武丁编码使得一系列问题能以更优雅且统一的方式得到解决，例如：

（1）二阶算术在（T，≤T）的理论中可翻译，因而T的理论是不可判定的；

（2）T结构是刚性的（rigid），当且仅当T可与二阶算术相互翻译；

（3）T上的自同构在一个倒锥体（cone）上是等同函数；

（4）存在一种对每个T上自同构的算术表达，因而至多有可数个T上的自同构。

辛普森（Simpson，Stephen G.）在（Simpson，1977）中利用斯佩克特对可数理想的编码证明了二阶算术可以被翻译到T的一阶理论，因此，T的一阶理论是不可判定的。利用斯拉曼-武丁编码定理可以更直接地将二阶算术翻译到T中。例如，我们可以在T中定义一个性质P，使得满足的参数序列编码了算术结构（N，+，·）在T中的一个同构像。显然，在T中可以定义关系“编码的集合是编码的集合的子集”：

由此，二阶算术量词如...可以被解释为T中关于参数的一阶量词：

将二阶算术翻译到T理论中的关键是将每个自然数集X对应为在T中编码（N，+，·，X）的一类参数组。而要将T理论翻译到二阶算术中，需要把每个图灵度x对应于其中的一个代表X∈x。如果在T中可以（在编码的语境下）定义“X是x的代表”这一关系，则称T可与二阶算术相互翻译（biinterpretable with second ordered arithmetic）。

定义　2.14（可与二阶算术相互翻译）　度结构（，≤）可与二阶算术相互翻译，当且仅当下述关系在（，≤）中可定义：对任意⇔自然数集X是x的代表，且（在定理2.13意义上）编码X。

我们称一个结构是刚性的，当且仅当它没有非平凡的自同构。一阶或二阶算术结构都是刚性的。可以证明，如果T可与二阶算术相互翻译，那么T和二阶算术结构一样也是刚性的。假设π：T→T是自同构，由此，可以引导出实数集上的自同构π*：P（ω）→P（ω），满足如果→c是X的编码，那么π*（X）=所编码的集合。由于二阶算术结构是刚性的，π*是等同映射，因此，和编码了同一个自然数集X。任给x∈T，X∈x，由于关系R可定义因而在自同构π下保持，。显然，如果且，那么x1=x2，所以π（x）=x。

斯拉曼和武丁证明（Slaman and Woodin，2005）T是刚性的，当且仅当T可与二阶算术相互翻译。并猜想，图灵度结构T是刚性的。

在考虑（全局）图灵度结构的同时，现代递归论也着力研究局部的图灵度结构和对应于其他归约概念的度结构，例如，在上一节中介绍的递归可枚举的图灵度结构。我们知道，波斯特在（Post，1944）和（Kleene and Post，1954）中构思的方法都没能构造出介于停机问题和可计算之间的图灵度。弗里德贝格（Friedberg，1957）和穆奇尼克（Muchnik，1956）发明了被称作优先方法（priority argument）的技术构造了一对互相不可归约的递归可枚举集，最终解决了波斯特问题。优先方法被推广并用于构造各种递归可枚举集。萨克斯利用改造过的优先方法证明了递归可枚举的图灵度是稠密的，即对任意递归可枚举集A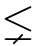TB，存在递归可枚举集C，使得ATC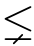TB（Sacks，1964）。因此，至少递归可枚举的图灵度结构与全局图灵度结构不是初等等价的。

优先方法

优先方法的技术最早被用于构造一对互相不可归约的递归可枚举集。显然，这对集合既不是递归的，也不是递归可枚举完全的，而是属于介于两者之间的“不可解的度”。

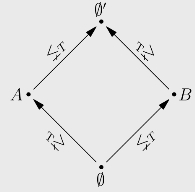
图2.8　A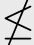TB且BTA

使用优先方法生成集合，往往是为了满足若干组要求，而为了满足其中一组要求，在生成集合过程中所做的操作有可能“损害”到先前为了满足其他要求所做的努力，因此，有必要将这些要求按优先级排序，并且在构造中设法要求在满足优先级低的要求时不能损害到先前为满足高优先级要求所做的努力。如此，高优先级的要求被满足后就难以再被损害，并由此逐渐满足所有要求。

在弗里德贝格的证明中，需要递归地枚举出A，B并满足两组需求，分别使得A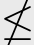TB且BTA（见图2.8）。具体而言，需要满足需求：

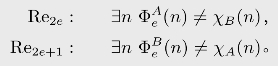
这些需求的优先级以R0，R1，...，R2e，R2e+1，...的方式排列。为满足需求Re2e，设法找到n使得以As为神谕得出的回答是n /∈B，即=0，然后反将n添加进B。注意，如果不存在这种情况的话，Re2e自然满足。为体现优先级，在为Re2e做出努力后需要设置屏障，阻止以后在处理某些低优先级的Re2d+1时干扰==0这一计算结果的自然数放入A。R0在构造中一旦被满足就最终被满足，而R1被满足后可能在处理R0时被损害一次，R2则至多被损害三次就最终被满足。依此类推，每个需求至多被损害有穷次，最终所有要求都会被满足。因此，弗里德贝格的论证又被称作“有穷损害优先方法”。

类似地，有些研究聚焦于图灵度结构的一些理想，如T（≤T0′），即所有集合的图灵度，以及算术可定义集的图灵度∪n＜ωT（≤T0（n））。T（≤T0′）比递归可枚举的图灵度更接近T。例如，（Spector，1956）的多数结论都在T（≤T0′）中成立：存在极小元，非稠密，存在精确对。斯拉曼和索斯科娃（Soskova，Mariya I.）证明（Slaman and Soskova，2015）：T（≤T0′）与全局结构一样有至多可数个非平凡的自同构，并且T（≤T0′）是刚性的当且仅当它可与一阶算术相互翻译。自然数集X是一阶算术可定义的，当且仅当存在n＜ω使得X≤TØ（n）（图灵跃迁的n次迭代）。算术可定义集的图灵度结构虽然有无穷上升的图灵度序列，但并不与T初等等价。贾库什（Jockusch，Carl G.）和索阿雷（Soare，Robert Irving）在（Jockusch and Soare，1970）中证明了每个0（n）都不是极小覆盖，即

贾库什在（Jockusch，1973）中证明了在T中存在一个倒锥体的极小覆盖，即T满足

在T（≤T0（ω））中，每个倒锥体都包含几乎所有0（n），因而不满足（2.3），也因此和T满足不同的一阶理论。

不同的归约概念也导致相应的度结构呈现出完全不同的性质，例如多到一可归约概念对应的度结构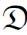（m，≤m）。直观上，这个结构比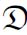T更细密。显然，m的基数是。可以证明，m满足：

（1）具有可数前驱性质；

（2）是一个拥有最小元的向上的分配半格（见第68页）；

（3）对任意基数≤且满足（1）、（2）的半格L，如果存在L的一个理想I和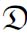m的一个理想J之间的同构π：I→J，那么π可以被扩张成π*：L→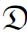m，将整个L嵌入为m中的一个理想。

并且，m是满足上述性质的唯一结构（Ershov，1975）（Palyutin，1975）。此外，m上存在个不同的自同构，其中可定义的元素（单点集）只有最小元。

另一方面，定义自然数集A超算术可归约于B（hyperarithmetical reduction），当且仅当以B为参数存在和的二阶算术公式可分别定义A。超算术可归约对应于相比T更“粗糙”的度结构h。可以证明，h可与二阶算术相互翻译，因而是刚性的。