K和K0虽然不是可计算的，但仍然可以“能行地生成”。例如，我们可以编写程序逐一尝试运行Φe（e）^[4]，一旦发现Φe（e）↓，就把该指标数e记录下来。可以说，该程序随着时间的推移机械地生成集合K。这类集合在现代术语下被称作递归可枚举集或计算可枚举集（recursively/computably enumerable sets）。直观上，所有递归的集合都是递归可枚举的。而递归可枚举集K0，K则不是递归的。因此，递归可枚举是一个更宽泛的概念。波斯特（Post，Emil Leon）在（Post，1944）中对递归可枚举的研究被认为是“对计算可枚举集现代研究的开始”（Soare，1999）。

在（Post，1944）中，波斯特使用“生成的”（generated）集合来表示直观上的递归可枚举集概念：

生成的集合……只需要该集合的每个元素作为某个先定的能行过程的结果被在某个时刻写下来并被标记为属于这个集合。正如人们所理解的，一旦一个元素被放入这个集合，它就一直在那了。（Post，1944，p.286）

而将正式的递归可枚举集概念定义为一个递归函数值域。此外，波斯特还定义了“正规系统生成的（generated by a normal system）集合”来刻画直观上的“生成的集合”概念。波斯特宣称正规系统生成的与递归可枚举的是等价的，两者都刻画了直观上的“生成的集合”概念，这似乎是丘奇-图灵论题的递归可枚举版本。波斯特的论证虽然简短，但也包含了图灵论证（见第23—26页）的主要策略，即直接诉诸直观的论证和诉诸经验的（已有的关于生成的集合的严格刻画都是等价的）论证。有趣的是，波斯特不满克莱尼（Kleene，Stephen Cole）用“论题”（thesis）来指代关于严格定义与直观概念等价的判断，而倾向于使用“自然律”（law）来描述这里的情形。无论是丘奇-图灵论题还是波斯特自然律，其意义在于让现代递归论学家可以用更自然语言化的书写风格来进行严格的证明，而无须在每个证明中都把完整的图灵机或计算机程序编写出来。波斯特这篇文章本身就是这种写作风格的模板。

递归可枚举集的等价定义

定义　2.1　称自然数集A⊂ω是递归可枚举的，当且仅当A=}Ø或存在一个递归函数f，使得。

显然，递归可枚举集是直观上可以机械地生成的。只需要采用计算f的程序Φ，逐一输入0，1，2，...，并将运算结果Φ（0），Φ（1），Φ（2）记录下来就可以了。可以证明，递归可枚举有许多等价的定义。

引理2.2给定自然数集A⊂ω，下列命题等价。

（1）A是递归可枚举的；

（2）存在一个部分递归函数f使得A=ran f；

（3）存在一个部分递归函数f使得A=dom f；

（4）A是集合，即存在一个Σ1公式∃yφ（x，y）在一阶算术结构中定义A：

因为递归可枚举集也可以被等价地定义为部分递归函数的值域或定义域，而对应于部分递归函数的程序集是可枚举的，所以递归可枚举集类本身也是在一定意义上可枚举的。例如，定义

那么，就枚举了所有的递归可枚举集。

此外，值得注意的是，集合的计算复杂度与它们的可定义性具有密切的相关性。我们知道，的集合都是原始递归的，而递归可枚举集都是集。容易证明，如果集合A和它的补集ω\A都是递归可枚举的，当且仅当A和它的补集都是递归的。因此，递归集合就是的集合。所以，在定义公式复杂度的意义上，递归可枚举集就是紧接着递归集的下一类集合。

然而，定义复杂度直观上是一个较粗略的划分方式。波斯特在（Post，1944）中为递归论学家提出的问题本质上是：在递归可枚举集中是否还存在不同的计算复杂度，或按照波斯特的原文——“不可解的度”（degree of unsolvability）。后人称之为波斯特问题（Post’s problem）。如果所有非递归的递归可枚举集都具有本质上相同的计算复杂度，那么计算复杂度可能就没有什么独立的意义，而是可以被定义复杂度替代的了。反之，如果能发现递归可枚举集中本质上不同的非递归的计算复杂度，无疑将大幅增加人们对不可计算集合计算复杂性的理解。

回到之前定义的停机问题K和K0。容易证明，停机问题是所有递归可枚举集中“最复杂的”。任何递归可枚举集都可以图灵归约为停机问题。任给递归可枚举集We，根据（2.1）定义，要回答自然数n是否属于We，只需要问（e，n）是否属于K0，或者p（e，n）（见第56页）是否属于K就行了。此时，可以称递归可枚举集K（或K0）是递归可枚举完全的。由此，波斯特问题就可以更清晰地表达为：是否存在计算复杂度严格小于停机问题的非递归的递归可枚举集？

为了在递归可枚举集中寻找不同的计算复杂度，波斯特的策略是刻画尽可能严格的归约概念，由此带来更加精细的复杂度划分。

波斯特首先定义的是多到一可归约（many-one reducibility）。称一个集合A多到一可归约于B（记作A≤mB），当且仅当存在一个递归的全函数f：N→N使得对任意自然数n，n∈A当且仅当f（n）∈B。^[5]也就是说，当我们想知道一个自然数n是不是在A里面的时候，我们只需要问B一个问题，即f（n）在不在B里面。显然，多到一可归约是比图灵可归约更严格的概念，后者并不限制问神谕问题的数量。但依然容易证明，在多到一可归约关系下，停机问题仍是递归可枚举集中最“复杂”的。事实上，在说明停机问题是递归可枚举完全的论证中，为判定n是否属于We，确实只问了K（或K0）一个问题。也因此，递归可枚举K≤mK0且K0≤mK。此时，可以称K与K0是多到一归约等价的（many-one equivalent），记作K≡mK0。

为寻找在多到一可归约概念下位于可计算与停机问题之间的计算复杂性，波斯特注意到停机问题的一个性质：K不仅是不可计算的，并且是能行地不可计算的。由于K本身是递归可枚举的，那么K可计算当且仅当它的补集也是递归可枚举的。但是对任意包含于K的补集的递归可枚举集We⊂ω\K，它的指标e本身就见证了We/=ω\K。因为，如果e∈We，即Φe（e）↓，那么e∈K，与We⊂ω\K矛盾。所以，e/∈We并且由此可证e∈ω\K。换句话说，停机问题K以一种很强的方式成为非递归的集合。波斯特将具有这种性质的集合定义为创造集（creative set）。

定义　2.3（创造集）　称递归可枚举集C是创造集，当且仅当存在一个递归的函数f，对每个递归可枚举的集合We⊂ω\C，都有f（e）/∈We且f（e）/∈C（见图2.3）。

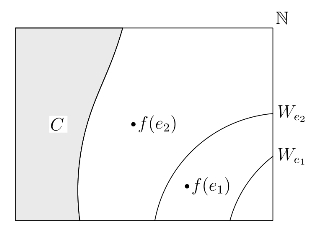
图2.3　创造集：能行地非递归

波斯特认为这个性质是对哥德尔不完备性定理的推广，显示了数学不断创造的本质，创造集由此得名。创造集也确实如人们对它的直观一样是递归可枚举集中非常不可计算的。事实上，可以证明，所有创造集在计算复杂度上与停机问题没什么区别。即，对任意创造集C都有C≡mK。因此，任何递归可枚举集都多到一可归约于任何创造集，任何创造集都是在多到一可归约下完全的。

接着波斯特根据“创造集”的特征“量身定做”了一种被称作单集（simple set）的递归可枚举集。

定义　2.4（单集）　我们称一个递归可枚举集S是单集，当且仅当它的补集ω\S是无穷的，并且S与所有无穷递归可枚举集相交（见图2.4）。

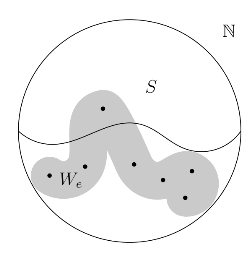
图2.4　单集

显然，一个单集的补集不是递归可枚举的，因而它不是递归的。同时，单集的补集非常“薄”，以至于无法将任何创造集C或它的补集ω\C整个嵌入其中，也就不能以这种最直接的方式将是否属于C的信息编入S。容易证明，任何创造集都不能多到一可归约于一个单集。接着，波斯特证明，确实存在一个单集。那么，这样一个集合的复杂度在多到一可归约的意义上就严格位于递归集和停机问题之间了。(www.daowen.com)

单集见证多到一可归约在递归可枚举集类上是非平凡的

首先，证明任何创造集C不能多到一归约于一个单集S。假设S是单集，递归函数f见证C是创造集，且存在一个递归函数g：C→S见证C多到一可归约于S，那么，对任意S补集的一个有穷子集A0，f-1[A0]是C的补集的一个递归可枚举的子集，并且我们可以能行地写出枚举f-1[A0]的程序，记作。因此，我们也可以能行地找到一个在C的补集中而不在f-1[A0]中的元素，而就是一个在S的补集中却不在A0中的元素。由此，我们可以生成一个与S不相交的无穷递归可枚举集，矛盾。

要构造一个单集并不难，只需要逐一枚举所有的递归可枚举集合，然后在每个（非空）递归可枚举集中取一个元素放入S。为了确保ω\S是无穷的，只需要规定每次放入S见证S与We相交的元素＞2e就可以了。对任意自然数m，考虑区间[m+1，2m+2]，其中包含m+2个自然数。而只有当e＜m+1时（一共有m+1个这样的e），S与We相交的见证才会被放进S。所以每个区间[m+1，2m+2]中都会有不属于S的元素，ω\S无穷。又由于我们只需要保证S与所有无穷的递归可枚举集相交，上述规定并不会令我们遗漏什么。

然而，多到一可归约作为刻画相对可计算性的归约概念显然过于严格了。似乎没有理由要求在每一次计算中只能问神谕一个问题，还要求神谕的回答和求解问题的答案同为真或同为假。那么，单集是否能在更合理的归约概念下作为在可计算与停机问题之间存在其他计算复杂度的见证呢？遗憾的是，波斯特紧接着就构造了一种单集，它们在图灵可归约意义上是递归可枚举集中最复杂的，也即可以用来计算停机问题。这意味着，第一，单集的存在无法作为波斯特问题正面解的一个见证；第二，多到一可归约作为对相对可计算概念的刻画的确太苛刻了，许多直观意义上相对可计算的在多到一可归约意义上是不可计算的。

接下来，一个自然的想法就是稍微放宽相对可计算概念的要求。波斯特定义了一种介于图灵可归约与多到一可归约之间的概念——真值表可归约（truth table reducible）。

定义　2.5（真值表可归约）　称集合A真值表可归约于集合B（truth table reducible，记作A≤ttB），当且仅当存在一个能行的程序t，当我们希望知道n是不是在A里面时，我们用t计算出一个真值表t（n），再比对B，取t（n）中与B的前段相符的那行作为答案（见图2.5）。

图2.5　真值表归约

与多到一可归约定义中只能问神谕集B的一个位置的值相比，真值表可归约允许一次性问B中任意有穷个位置的值。但这个概念相对图灵可归约还是有更多的限制。与图灵可归约不同，真值表可归约只有问一次问题的机会，不允许根据B的反馈调整下一个要向B咨询的问题，而这种“互动”在相对可计算概念的直观中似乎是应该被允许的。可以类似地证明，存在一个单集在真值表可归约意义上是所有递归可枚举集中最难的。这说明，真值表可归约的确是比多到一可归约更宽松的相对可计算性概念，也进一步佐证了多到一可归约作为对相对可计算性概念的刻画过于严格了。

构造“最难的”单集

任意给定创造集C，我们试图能行地生成一个单集SC将计算C所需要的信息编入其中，这样，就可以用SC作神谕计算所有递归可枚举集了。

第62页中给出了一个生成单集S的机械方法，并且任意形如[m+1，2m+2]的区间都不会被S“占满”。考虑区间序列

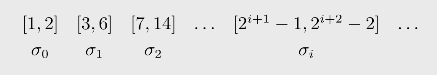
定义SC为下述程序生成的集合：同时运行生成S和C的程序。每当一个自然数e被放入S中，将e放入SC。每当一个自然数i被放入C中，将整个σi区间中的数全部放入SC。容易验证，这样生成的SC确实是单集，并且携带了计算C所需要的信息：问i是否属于C，只需要看是否区间[2i+1-1，2i+2-2]中的自然数全部在SC就行了。换句话说，利用SC计算C时，针对每一个i，只需要一次性问SC关于[2i+1-1，2i+2-2]的问题就可以了。所以，我们实际上证明了C≤ttSC。

寻找在真值表可归约意义上介于可计算和停机问题之间的计算复杂度会更困难。波斯特设法刻画了比单集具有更“薄”补集的超单集（hypersimple set）。

定义　2.6（超单集）　称集合H是超单集，当且仅当它是递归可枚举的、它的补集是无穷的，并且对任意由两两不相交的有穷自然数集组成的无穷递归可枚举集合族X^[6]，存在s∈X使得s⊂H（见图2.6）。

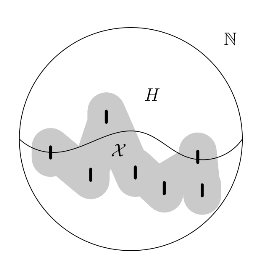
图2.6　超单集

显然，超单集是单集。类似地，可以证明，存在一个超单集。而超单集的定义使得创造集的信息不能以最直接的方式编入一个超单集。事实上，可以证明任何创造集都不能真值表归约于一个超单集。因而，超单集的存在似乎有可能成为波斯特问题正面解的一个有力的候选。然而，再一次，波斯特证明了超单集可以与停机问题图灵等价。这个方向上的努力再一次失败，并且暗示了真值表可归约仍然是过于严格的刻画，那么接下来自然的想法是定义更严格的概念，如超超单集（hyper-hyper-simple set）。

定义　2.7（超超单集）　一个递归可枚举集H是超超单集，当且仅当它的补集是无穷的，并且对任意两两不交的递归可枚举集序列

（f是递归函数），总存在Wf（n）⊂H。

超超单集显然是超单集，并且有更“薄”的补集。波斯特在文章中并没有构造出一个超超单集。麦希尔（Myhill，John）在（Myhill，1956）中提出了极大集（maximal set）概念，这是非递归的递归可枚举集中在一定意义上拥有最“薄”补集的一类集合，因此，极大集也是超超单集、超单集、单集。弗里德贝格（Friedberg，Richard M.）证明了存在极大集，因而也存在超超单集。耶茨（Yates，C.E.Mike）证明了存在与停机问题图灵等价的极大集。波斯特原本的计划是：定义一个性质P，使得满足该性质的非递归的递归可枚举X的补集非常“薄”以至于无法编入足够计算停机问题的信息，由此证明X的计算复杂度严格介于可计算集合与停机问题之间。耶茨的结果标志了上述计划的失败，因而波斯特最初的直观是错误的。^[7]

极大集

定义　2.8　称递归可枚举集M是极大集，当且仅当M的补集ω\M是无穷的，并且对任意递归可枚举W，要么W∩（ω\M）是有穷的，要么它的补集（ω\W）∩（ω\M）是有穷的。

极大集之所以得名，是因为它的补集不仅不能包含任何无穷递归可枚举集，甚至不能在忽略有穷例外的意义上包含任何无穷递归可枚举集。定义A⊂*B，当且仅当A\B是有穷的；A=*B，当且仅当A⊂*B且B⊂*A。令M是极大集。如果存在无穷递归可枚举W⊂*（ω\M），即W∩M是有穷的，那么W∩（ω\M）就是无穷的了。一个无穷的递归可枚举W总是可以分成两个不交的无穷递归可枚举W1，W2使得W1∪W2=W。由此，W1∩（ω\M）和（ω\W1）∩（ω\M）都是无穷的，矛盾。可以类似地证明，极大集是超超单集。

令。令E*是E模有穷的商集，即而每个，那么结构（E*，⊂*）就是（E，⊂）模有穷的商结构，而任何极大集都是结构（E*，⊂*）中的极大元。

M是极大集。

显然，波斯特在这篇文章中并没有解决自己提出来的问题，并且波斯特最初的直观被证明是有误的。十多年后，弗里德贝格和穆奇尼克（Muchnik，Albert Abramovich）分别独立解决了波斯特问题（见第74页）。然而，他们的解决方式并没有按照波斯特规划的上述路线。但是，波斯特在（Post，1944）中提出的诸概念以及基于其上的研究计划实际上开启了现代递归论研究。

简要回顾下波斯特（Post，1944）这篇文章的形式。除了前文中提到的关于递归可枚举集正确刻画了生成集直观的辩护，文章主体部分试图分析的是“不可解的度”以及相应的归约概念。图灵运用带神谕的图灵机给出了对相对可计算归约概念的一个精确的数学定义。波斯特显然非常认同，但是仍有遗留的问题。其一是，如何为这个刻画提供辩护。其二是，图灵归约虽然是一个毫无歧义的精确定义，但不自然意味着我们就能清楚地掌握这个概念的外延。反倒是，我们对它的外延几乎一无所知。波斯特的规划就是要（首先在递归可枚举集的范围内）搞清楚这个外延，并且相信随着我们对其外延的认识越来越清晰，也就会有越来越强的信心认为图灵的这个刻画是正确的解释。为此，波斯特还提出了其他可能的对相对可计算归约概念的刻画，通过证明这些刻画的一些性质显示出这些刻画未能正确反映人们对“相对可计算性”的直观，而这些又进一步佐证图灵可归约刻画的正确性。就这点而言，波斯特的论证是有说服力的，并且这与在第一章中提到的早期分析哲学的论证形式相符。