图灵1937年的文章（Turing，1937）为通用计算机的出现奠定了理论基础，也使现代理论计算机科学成为可能。从此，人们可以用图灵给出的模型来分析可计算函数或集合的计算复杂度。一个集合是可计算的，当且仅当存在一个计算机程序（或图灵机）来判定任何一个自然数是否属于这个集合。例如，所有素数组成的集合是可计算的；在给定编码下，所有命题逻辑重言式是可计算的。

可计算的函数或集合

由于每个计算机程序（或图灵机）都可以写成01序列σ∈2＜ω，因此可以用自然数编码计算机程序。令是所有计算机程序的典范枚举。由于任何有穷自然数序列都和单个自然数一样只携带有穷信息，可以被能行地编码成自然数，因此，在递归论中不需要区分它们。不妨假设所有程序的输入输出都是自然数。令e，n，s是自然数，一般用Φe，s（n）↑表示，程序Φe在输入n下运行s步^[3]后没有停机，用Φe，s（n）↓表示程序Φe在输入n下运行s步内停机，用Φe，s（n）↓=m表示在s步内停机并输出m，而用Φe（n）↓（=m）表示∃s Φe，s（n）↓（=m），即程序Φe在输入n下会停机（并输出m）。每个程序Φe都定义了一个部分可计算函数或部分递归函数（partial computable/recursive function）fe（在上下文清楚的情况下，也用Φe指代函数fe）：

一个自然数上的（全）函数f：Nn→N是可计算的（又称作递归的），当且仅当存在一个计算机程序Φe，对任意输入n，Φe（n）↓=f（n）。一个自然数集合A⊂N是可计算的或递归的，当且仅当它的特征函数

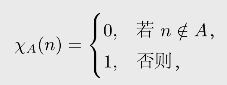
是可计算的。

然而，进一步的考察不难发现可计算的集合是一类非常特殊的集合。且不论自然数集有连续统那么多个，而可计算的集合限于程序的基数只有可数多个。在理论研究实践中，人们也经常会遇到不可计算的集合。例如，图灵在（Turing，1937）中用对角线法证明所有生成可计算函数的程序组成的集合是不可计算的。此外，给定一阶逻辑语言，其中逻辑有效式的集合是不可计算的；令N=（N，+，·，0，1）表示一阶算术结构，那么一阶算术真命题也是不可计算的。

对角线法

康托尔（Cantor，Georg）曾使用对角线法证明连续统的基数。反设，可以用自然数枚举所有无穷01序列。定义无穷01序列y，使得对任意n＜ω，y（n）=1-xn（n），那么y与任何一个xn在第n位不同。所以，y不在枚举中，矛盾（见图2.1）。

图2.1　对角线法

类似地，假设是一个可计算的集合，那么，我们就可以设计一个程序Φ：对任意输入e，调用程序判断是否e∈C。如果是的话，运行Φe（e），并输出1-fe（e）；如果不是的话，输出0。这样，Φ就定义了一个可计算的函数f，并且f与每个可计算的函数都不一样。

因此，有必要将视野扩展到可计算集合之外，更一般地考察自然数集的复杂度与可计算性。在讨论复杂性问题时，人们常使用多项式可归约概念来分类各种可计算集合。类似地，在讨论不可计算集合的复杂度时也需要使用各种归约概念对集合分类。例如，利用对角线法可以证明，集合(www.daowen.com)

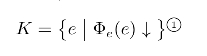
①在下文定义图灵跃迁运算X′（见定义2.9）后，又将K记作Ø′。

（即所有满足“e号程序在输入e下停机”的编号e组成的集合）是不可计算的。K也被称作停机问题（halting problem）。定义

似乎K0被称作停机问题更符合直观，但可以证明这两个集合在下述意义上是等价的。假设存在判定任意自然数对（e，n）是否属于K0的程序，那么也存在程序来判定任意自然数e是否属于K，因为只需要运行前一个程序并输入（e，e）就可以了。反过来，假设存在判断e是否属于K的程序。要判断任意（e，n）是否属于K0，首先可以能行地算出程序Φp（e，n）的编码p（e，n）。Φp（e，n）这个程序在任何输入下均执行Φe在输入n下的动作，即特别地，Φe（n）↓当且仅当。因此，判断（e，n）是否属于K0，只要算p（e，n）是否属于K就行了。所以，K和K0实际上是同样复杂的一类集合。

递归论中最常使用的归约概念是图灵在他的博士论文（Turing，1938）中首次提出的图灵归约（Turing reduction）概念。图灵对可计算性的定义基于图灵机这个数学模型：一个集合或函数是可计算的当且仅当有一台图灵机来计算它。图灵通过将图灵机概念推广为带神谕（oracle）的图灵机而定义了相对可计算性概念：我们说集合A相对于集合B是可计算的，当且仅当存在一个带神谕的图灵机以B的信息为神谕能计算任何一个自然数是否属于A。

带神谕的图灵机

带神谕的图灵机相比普通图灵机多了一个只读功能的头用来读取存储神谕的纸带（见图2.2）。它的每一个指令是一个六元组，根据当前（1）内部状态、（2）读写头读到的符号和（3）只读头读到的符号做出下列动作：（1）读写头改写一个符号或向左/右移动一格；（2）只读头向左/右移动一格或不动；（3）改变内部状态。

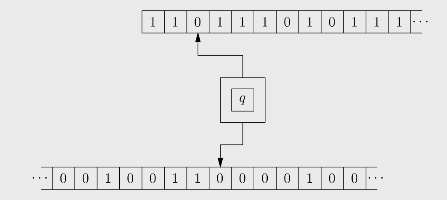
图2.2　带神谕的图灵机

在现代术语中，为区别于别的归约概念，一般以A图灵可归约于B（记作A≤TB）来表示存在以B为神谕的图灵机来算A。如果A≤TB且B≤TA，则称集合A与B是图灵等价的（Turing equivalent，记作A≡TB）。容易验证，≡T确实是一个等价关系。在上面的例子中，K与K0就是图灵等价的。