根据冯·赖特的报道（von Wright，1993，p.19），塔斯基曾苦恼于如何让数理逻辑在伯克利的数学系得到尊重。按照金森（Kanamori，Akihiro）的说法，今天的集合论已经是“一个独特的数学领域”，是“现代的、成熟且高度技术化的（sophisticated）领域”（Kanamori，2008）。不仅如此，数理逻辑主要分支都已基本形成一套较稳定的问题域和技术方法。可以说，数理逻辑已经确立了它作为一门数学分支的地位，塔斯基的目标在相当程度上实现了。然而，无法回避的现实是，今天的数理逻辑研究作为数学的一个分支在数学界的地位并不能令很多逻辑学家感到满意。数理逻辑即使获得一些同行的关注，也仅仅是因为它提供了一些有趣的工具，例如模型论方法在代数和分析中的应用。这与数学基础研究在20世纪初所受到的广泛而深入的关注无法相提并论。

当代数理逻辑研究本身的艰深及其相对其他数学分支几乎可以忽略的经济上的实用性，使得许多学者在选择方向时对这个领域敬而远之。这在客观上降低了数理逻辑研究在整个数学界的存在感。更严肃地说，数学家们对于基础问题变得兴味索然或许是出于这样一些考虑：公理化方法对罗素悖论的回应目前看来并没有什么问题；想要一劳永逸彻底解决基础问题似乎又是不可能的；而实际的数学工作甚至在安全得多的基础上就足以完成。基础问题既不迫切也无法立即解决，在其上耗费大量智力资源也就是不明智的了。这也是1.2.3小节中所描绘的新形式主义者的思想来源。

然而，那些基础问题仍然在那儿，而且在这个人类的秘密被逐一揭开并由机器实现的时代变得更加尖锐和迫切。数学家要证明他们的工作与一台定理枚举机有本质的区别，就不能将他们的工作仅仅局限于那些关于是否“存在一个从公理系统Λ到公式φ的证明”这样的问题。^[44]数学家们如果仍然相信他们的工作是有关真理的，就不得不面对“为什么选择Λ这个公理系统，而不是其他的”，或者“为什么公理σ是真的或自明的”这样的问题。即使是同一个公理系统的定理，数学家会认为有一些比另一些更有趣、更丰富或更深刻。这或许也不是一台给定的机器能辨别的，而数学家则宣称对此有直观，但这些直观却与数学这门特殊的学科引以为傲的清晰性与严格性相去尚远。人们的好奇心和追求普遍的冲动仍然会时不时地迫使人们面对这些问题。

事实上，驱动当代数理逻辑研究的许多问题仍然可以被追溯到那些关于数学基础的核心问题，只是当代数理逻辑的很多成果确实让人们在面对这些问题时感到空前的茫然无措。新兴的反推数学（reverse mathematics）计划（Simpson，2010）仍然是为了帮助解决公理选择的问题。起初，人们发现常见的公理系统可以按照一致性强度乖巧地排列成一个由弱到强的线序（两两可比），即哥德尔层谱（Gödel hierarchy，见图1.4）。越强的系统能证明越多的定理，但不一致的危险也越高。反推数学就是要告诉人们选择某个公理系统到底意味着什么（可以保留而又必须放弃哪些经典数学定理）。但随着研究的推进，人们发现公理系统线性排列现象绝非事情的全貌。大量中间系统被发现，并且许多是两两不可比的。于是现在的图景，仅系统ACA0与RCA0之间的主要公理系统就构成如图1.5所示的繁杂景象。

而在ZFC之上，哥德尔曾希望ZFC+LCA（LCA指越来越强的大基数公理）能构成一排通向完备数学真理的阶梯，解决所有已知的独立问题（Gödel，1947）。但自1963年科恩发明力迫法（forcing）之后，用ZFC+LCA解决连续统假设的梦想破灭了。^[45]不仅如此，更多独立于ZFC甚至ZFC+LCA的命题相继被发现，它们成立于各种各样的集合论宇宙中。如何解释集合论学家们在这些集合论宇宙中对各种集合概念的“经验”对认为只存在唯一一个“集合”概念的传统实在论是一个空前的挑战（Hamkins，2012）。

面对这幅乱局，已有的数学哲学立场都显得捉襟见肘。数学真到底意味着什么，一则数学命题何以是真的，又或者我们究竟能否无矛盾地谈论数学真？这些无论如何都无法回避的数学基础问题不仅没有解决，反而在当代显得更加扑朔迷离。无论出于对这些问题本身的好奇还是对数理逻辑这个领域发展的关切，复兴数学基础研究都是值得考虑的选项。而纯数学的方法被证明在处理基础问题时是不够的。因此，或有必要以更开明的态度来考量那些看起来不如纯数学方法那样严格的思考（例如，哥德尔关于心灵、概念、绝对证明的思想），并尽力使之严格。而后者也是分析传统下的哲学的主要工作。

图1.4　哥德尔层谱^[46]

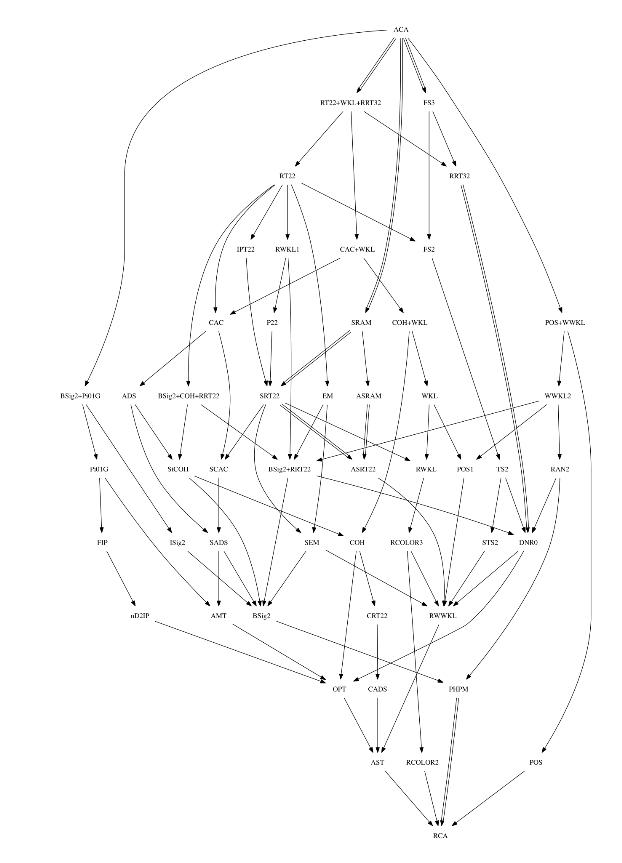
图1.5　反推数学的动物园^[47]

一个世纪前人类对理性或“人类精神”的自信达到了一个巅峰，希尔伯特宣布人类将战胜“不可知”。然而此后的一百年间，伴随着一次次人类社会的浩劫和种种试图把握普遍真理的挫折，人们渐渐失去了对理性的信心。哲学家们又开始热衷于为可知的王国划界树墙，并宣布外面的世界“不可知”。

然而，“不可知”本身仍然要求一个证明。哲学家要么通过精巧的辞令回避了这个要求，要么给出了无效的论证。蒯因将其自然主义——彻底的经验主义的立场建立在对分析性不可判定的断言上，而对后者的论证最终落实于“存在一个可以划定的边界是经验主义的非经验的教条”（Quine，1951，p.34，楷体由笔者添加）。显然，这个论证要么仅在预设经验主义的前提下才有效，要么就是一则循环论证，非经验的不可知因为它是非经验的。按理说，《经验主义的两个教条》的影响应该仅仅是经验主义内部的事情，却成为了“整个20世纪哲学最重要的一篇论文”（Godfrey-Smith，2009，p.31）。这进一步印证了这一百年中理性光芒的暗弱。

哲学家们关于“不可知”的另一种论证，是一种典型的经验论证。蒯因在展示了若干种尝试之后说道“关于分析的和综合的之间的边界只是尚未被划出”（Quine，1951，p.34，楷体由笔者添加），并由此得出，不存在这样的边界。经验论证在一定的范围内有其有效性，但是，在这里用“尚未知道”这一经验论据来论证“不可知”恰恰是不合适的。任何“可知的”在被知道之前都是“尚未知道的”。

当然，这类论证的流行还是反应了一个现实：理性在这一百年间取得的成就未能回应人们的期待，这或许才是理性主义的衰弱乃至数理逻辑与哲学互相远离的根本原因。然而，这一根本的原因却可能只是偶然的。面对这一现象，我们至少可以问三个问题：（1）人们是否公正地评价了理性在这期间业已所取得的成就？（2）人们的期待是否合理，在理性的拷问下，到底有哪些仍然是可以期待的？（3）人们又如何能取得更多的理智上的成就？笔者希望本书介绍的几则数理逻辑研究至少能从一个特定的视角对这几个问题给出一些积极乐观的回应。

【注释】

[1]日本战国时期大名织田信长在其即将完成天下布武的时候遭遇本能寺之变。传说其在临终时吟诵了表现平敦盛之死的《敦盛》（幸若舞）中的一段：人間五十年、化天のうちを比ぶれば、夢幻の如くなり、一度生を享け、滅せぬもののあるべきか？（人生五十年，与天地长久相较，如梦似幻；一度得生者，岂有不灭者乎？）后人常以“如梦似幻”比喻事业如日中天，却暗藏危机。

[2]食莲族（Lotus-eater），古希腊史诗《奥德赛》（Odýsseia）中记载的以某种类莲花植物为食的岛民。食用这种植物的果实会致幻，令人流连忘返。

[3]不可知（ignorabimus）。德国生理学家杜·波依斯-雷孟德（du Bois-Reymond，Emil）在其著作《论我们理解自然的极限》（Über die Grenzen des Naturerkennens：die sieben Welträthsel；zwei Vorträge，du Bois-Reymond，1903）中以拉丁格言ignoramus et ignorabimus（我们不知道，我们未来也无法知道）强调科学知识的极限。

[4]这是希尔伯特（Hilbert，David）1930年在格尼斯堡面向德国科学家与生理学家协会所做的演讲，翻译自（Smith，2014）。

[5]值得一提的是，弗雷格的概念是依附于语言的。

[6]对一阶完备性的现代刻画直到（Hilbert and Ackermann，1928）才出现，完备性问题才可解。

[7]这里讨论的是把数看作是事物的聚集（collection）的观点。

[8]注意，这个例子有赖于西方语言的一些特性，譬如英语中是“1000 leaves”，而汉语实际应该是“一千片树叶”，有表示单位的量词，不容易造成误解。不过，弗雷格在后文中对单位有专门的处理。

[9]值得注意的是，上述语境原则只能用以表明某种备选的解释是不合适的，而无法用以论证某种解释是正确的，或只能构成一个经验性的辩护。

[10]简单地说，用语义模型解释基础概念就是定义一个涉及有关概念的命题在哪些“场景”下为真。前一段中对实质蕴涵的解释实际上是提供了一个语义模型——真值表。而公理化方法表现为枚举一些含有有关概念的命题和推演规则，由此可以推出更多命题。这些命题是被预期为真的。公理化方法本质上就是直接提供一个能行方法来选出一些涉及该概念的被预期为真的命题。两种方法可以结合使用，既给出公理系统，也提供语义模型，再证明公理系统的推论在该语义模型下的解释都成立，即可靠性证明。

[11]譬如刘易斯对蕴涵的解释：只考虑真值的时候可以解释为实质蕴涵，而在考虑到内容和含义的日常理解中，往往应该解释为严格蕴涵。又例如罗素对指称短语的解释实际就是一个函数，以含有该短语的命题为输入（语境），以改造后的命题为输出（解释）。

[12]现代模型论式的真定义直到（Tarski and Vaught，1957）才被完整给出。

[13]首次发表于（Gödel，1929）。

[14]图片来源：https：//en.wikipedia.org/wiki/Pascal’s_calculator。

[15]一个自然数上的n元函数是一个特殊的自然数上的n+1元关系，它将每个n元自然数组对应于至多一个自然数。参见（郝兆宽、杨睿之、杨跃，2014，p.10）。

[16]此即希尔伯特纲领（Hilbert’s Program）。哥德尔不完备性定理、塔斯基真不可定义定理以及将要提到的图灵（Turing，Alan M.）等人的工作从各个层面证明，希尔伯特纲领是不切实际的。

[17]亚里士多德关于灵魂与身体的区分是其形式与质料（matter）之区分的一个实例。(www.daowen.com)

[18]显然，图灵这里的数（number）是指类似于实数的无穷01序列，它们也可以被看作是定义在自然数集上以{0，1}为值域的函数。在集合论中，所有无穷01序列组成的集合2ω可以构成康托尔空间（Cantor space），它与实数集R等势。

[19]函数f：N→{0，1}能被PA-表示，即存在一个一阶算术公式φ（x），对任意n∈N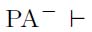，。图灵原文中的“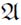定义（defines）a”就是我们这里所说的“一个公理系统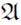可以表示一个函数a”。

[20]现在，computer往往被用来指称计算机或电脑。而在当时，computer指的是那些被雇佣以科学研究或其他目的做计算的人，且往往是女性。

[21]本质的区别指：按照不同的刻画，会导致有的函数在一种刻画下可计算，而在另一种刻画下不可计算。下同。

[22]集合A，B的对称差A△B=df（A\B）∪（B\A）。

[23]哥德尔批评图灵关于只有有穷可辨别的“心灵状态”的论证是一个哲学错误（philosophical error）。他说：“图灵完全忽视了的是，心灵在发挥作用时不是静止的，而是不断发展的……因此，尽管在每一个阶段我们能够处理的抽象词项的数量和精度可能都是有穷的，但两者（因而也包括图灵的可辨别心灵状态）都可能在运用这套程序的过程中收敛于无穷。”（Gödel，1972）

[24]蒯因在（Quine，1937）中提出了一套集合论公理，即现在被称作NF（New Foundation）的公理系统。蒯因本意在于使用尽可能少的公理模式。事实上，NF只包含一条外延公理和一组分层概括（stratified comprehension）公理模式。然而，NF并没有获得太多的关注，甚至它相对于ZF或相关系统的一致性还尚未解决。参见（Forster，2014）。此外，蒯因也撰写了若干本逻辑学教材：（Quine，1940）、（Quine，1941）、（Quine，1950）。但今天的逻辑学教学已不再使用甚至提及这些教材了。

[25]哥德尔在原文中使用B作为德文beweisbar（可证）的缩写。

[26]日常语言哲学与逻辑实证主义（logical positivism）同样拒绝形而上学，但基于完全不同的论证。后者试图通过逻辑分析严格区分基于事实而真与逻辑真，并说明形而上学判断不属于任何一种真，既非逻辑有效又无法被证实，因而是无意义的。

[27]即使在日常使用语言交流的过程中，语境也是随着交流的推进而变化的。可以说，对每一句话的使用都基于之前的对话所确立的语境，即需要事先的解释才能被理解。

[28]有关讨论和更多例子参见（Austin，1962）。

[29]克里普克关系结构语义学对模态命题赋值的值域是集合代数，也是一种布尔代数（Boolean algebra）。力迫法（forcing）生成的脱殊扩张（generic extension）也就是一种布尔值模型。

[30]可参考（Chalmers，2006）。

[31]如果蒯因坚持他的自然主义，那么就没有理由反对下面这种情况，即“同义”乃至“分析与综合的区分”有着自然主义意义上的实在基础，因而是可以通过经验观察来得到越来越清晰的认识的。

[32]一般认为，两者的目的不一样。词典定义的目的在于教会读者如何在语言中运用被定义项，而科学或哲学中定义的目的在于明确被定义项的意义（这点对阐释性定义和规定性定义也是一样的）。从形式上看，描述性定义总是“用熟悉的词汇来解释晦涩的术语”；字典定义则未必。

[33]值得一提的是，弗雷格认为至少在数学中，只存在规定性定义（见（Frege，1914））。如果承认这点，那么至少在数学中可以严格地刻画同义，从而可以严格定义哪些数学真是分析的了。

[34]一般来说，例如，一个一元谓词的外延是所有满足这个谓词所表达的属性的对象组成的类；而一个命题的外延就是它的真值。

[35]一般将这个命题的形式化写作：∀x（Bx↔¬Mx）。这当然不是一个在任何解释下都成立的逻辑有效式。

[36]例如，我们可以把一阶逻辑公理系统看作是对逻辑连接词和等次的隐定义，把集合论公理系统看作是对集合和集合的属于概念的隐定义。而显定义（explicit definition）是隐定义的一种，它由形如∀x（P x↔φ（x））的一个句子构成，其中P是被定义项。

[37]作为科学的一部分的本体论。

[38]在数学中，经过笛卡尔、魏尔斯特拉斯（Weierstrass，Karl）、戴德金（Dedekind，Richard）、康托尔（Cantor，Georg）、希尔伯特、策梅洛（Zermelo，Ernst）、图灵等数学家一系列的努力，我们有了关于许多数学概念在公理化集合论下的“标准”翻译，但仍然有许多数学概念并没有这样的标准翻译，例如我们将在2.2节介绍的随机性概念。而我们对作为基础概念的集合概念本身的刻画也是不完备的。

[39]即使直觉主义者不承认排中律，但他们仍然承认相当一部分逻辑有效式是分析的，而且他们所承认的逻辑有效式也有明确的边界。

[40]一般认为，公理化方法始于欧几里得（Euclid）《几何原本》（Elements），但对于什么是一个公理系统的严格刻画则依赖于形式语言。因此，现代公理化方法晚至20世纪初才定型。

[41]相比数学界，哲学界对弗雷格的发现更晚。

[42]卡尔纳普与蒯因都试图让所有经验科学使用统一的语言。卡尔纳普试图运用逻辑分析把科学理论还原为直接经验。蒯因的编制化理论见第39页。

[43]笔者并不否定经验科学及其方法可以并且已经为人类对诸多哲学问题的思考做出了贡献，而是希望不会因为一些哲学意见而使得另一些曾经十分有效的途径仅仅因为其在一段时间内未能继续提供更好的结果而被抛弃。

[44]引号中的命题可以通过编码翻译为关于是否存在具有某种有穷主义方法可判定的（或称原始递归的）属性的自然数的问题，这类问题/命题被称作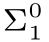的。

[45]科恩用以改变连续统基数的力迫法往往不会改变更大基数的大基数性质，因此，原证明几乎不加改变就可以用来证明Con（ZFC+LCA）→Con（ZFC+LCA+（¬）CH。详见第三章和4.2节。

[46]图表翻译自（Simpson，2010）。

[47]截至2013年人们所知道的以RCA0为基础证明的ACA0与RCA0之间主要二阶算术子系统的蕴涵及严格蕴涵关系。图片引自：http：//rmzoo.math.uconn.edu/。