20世纪30年代，数理逻辑领域的另一项重要成就是对能行（effective）或机械（mechanical）过程的刻画。

什么是能行的或机械的，看起来像是纯技术甚至是工程学的问题，实际上却与人对自身的认识这类古老的哲学话题密切相关。人类总是通过与周遭事物的比较、区分来认识自己的。例如，亚里士多德在《论灵魂》（De Anima）中，将灵魂的能力分为营养、知觉与心灵。植物具有营养的功能，动物具有营养与知觉功能，而人类拥有全部三种灵魂的能力。亚里士多德对于使得人类区别于其他物种的心灵的描述是：“灵魂的一部分，通过它灵魂认识（know）并理解（understand）。”（Shields，2016）

随着技术以及人对自身认识（如解剖学）的进步，人类自我认同遇到了新的挑战——机器。这并不是指某一台具体实现了的机器，而是机器这个概念。人们发现，但凡某个人类的机能可以被清晰明白地刻画出来，那么往往就能制造一台机器来实现它。例如，随着工业革命的发展，人类双手的的神秘性逐渐消失，人手的功能原则上都能使用机器来替代。更严峻的是，一般被认为属于心灵能力的智力活动也逐渐可以通过机器来实现了。帕斯卡（Pascal，Blaise）在17世纪中叶就设计制造了第一台能实际使用的加法计算器帕斯卡利娜（Pascaline）（见图1.1），以帮助其父亲完成计税工作。

图1.1　帕斯卡利娜（Pascaline）^[14]

无论是试图找出机器与人之间的差别还是试图论证人就是机器，都必须给出关于机器的严格刻画。要论证前者，就要找到某种人的能力并证明其不是机器的，这就需要明确给出机器的界线。而要论证后者，即说明人的并不比机器的更多，这甚至需要给出人的界限以及机器的界限。而对能行或机械过程的刻画，正是为机器划界的一种努力。

正如希尔伯特（Hilbert，David）所言：“只有当我们提炼出一门自然科学的数学内核并将其彻底揭开时，我们才算掌握了它的理论。”（见第1页）。运用这些理论解决问题，如工程上的问题，即通过该理论将有关问题归约为一类数学问题。更准确地说，往往是计算问题。例如，广义相对论（general theory of relativity）的核心是爱因斯坦场方程组（Einstein field equations）。而在GPS（Global Positioning System）中基于相对论效应对卫星和地面控制台原子钟由于相对运动和引力位（gravitational potential）所产生的偏差的校准就被归约为一套机械的计算程序内植于卫星、控制台和终端中（Parkinson and Spilker，1996，ch.18）。而我们日常应用中所进行的计算几乎全部可以被归约为或近似地归约为自然数结构上的算术运算。因此，当我们谈论机械过程时，我们实际谈论的是进行算术运算的机械过程。

那么，是不是所有算术问题都可以被能行地解决，或者说是不是任何自然数上的函数^[15]都有一个机械过程来计算它？抑或更保守一点，是不是凡是能被精确表达的问题或函数都能被能行地解决，正如希尔伯特等当时的数学家们所期望的那样？例如，加法函数通常被定义如下：

x+0=x,

x+(y+1)=(x+y)+1。

该函数的定义本身就暗示了计算它的过程。

希尔伯特的期待是可以理解的。要说明某个函数有能行的解法，我们只需要给出计算该函数的一个具体程序并证明该过程确实能正确计算这个函数就行了。要说明某类函数全都有能行的解法，往往只需要找到一个通用（universal）函数，并给出计算该通用函数的机械过程就行了。例如，塔斯基的真函数（将每句算术句子对应于它的真值）就是一个通用函数，而如果像希尔伯特所期望的那样，找到算术的一个公理系统并证明它是完备且一致的话，似乎就可以能行地解决所有算术问题了。^[16]然而，如果关于这些问题的答案是否定的话，我们该如何证明它？

看起来，我们只需要找到一个函数，并证明它不是能行或机械可计算的就行了。而要证明这点，即证明不存在一个能行或机械的过程能够计算这个函数，就需要遍历所有的能行或机械过程。遍历所有能行或机械过程的前提是：概念“能行的”或“机械的”有一个明确的界线。当我们说一个方法或过程是能行的或机械的时候，我们到底指的是什么意思？

首先，（1）一个能行的或机械的过程必须仅依赖一组有穷的指令集，每条指令也必须是有穷的。正如一个计算器就其基本单元的数量而言，一个计算机程序就其本身所含字符数而言是有穷的。否则，即如果我们允许无穷指令集的话，对任何函数，我们只需要把它全部信息（每组输入对应的输出）写入指令集，那么该指令集就成为可以计算该函数的过程了。而这显然不符合我们关于能行或机械过程的直观。

其次，（2）当我们说一个方法或过程能行地计算某个函数时，我们要求对任何一组输入这个方法都能在可识别的有穷步内得到期望的结果。或许有人会指出，某个机械过程可以每一步都有一个临时的输出并逐渐逼近期望的结果，或者说它每一步输出的极限就是期望的结果。但这里所考虑的是自然数上的运算，一个无穷的自然数序列有极限当且仅当它在有穷步内就收敛了。所以，期望的结果要么通过该方法在有穷步内就能得到，要么该方法在这组输入下无法得到期望的结果因而无法能行地计算目标函数。

再次，（3）能行或机械的方法只须严格按照其指令集运行即可保证成功，而不依赖任何洞见（insight）或灵机一动（ingenuity）。

有些定义还要求，（4）能行方法原则上能由一个人在不借助除纸笔以外工具的情况下独立完成。这里的“原则上”是指抽象掉一些具体的生理或物理上的限制，如人类的寿命、全世界木材总量（限制了纸张的数量）、宇宙物质总量等。这里有关的只是人类进行计算的那种能力，或者说是亚里士多德所说的那种名为心灵的灵魂，也即一种形式（form）。^[17]

以上四条标准的前两项比较明确。标准（4）有一定的争议。在这条标准下，任何机器的计算能力原则上不超过人类。而标准（3）是限制“能行”或“机械”概念的关键，却比较模糊。哥德尔不完备性定理、爱因斯坦场方程组、麦克斯韦方程组算不算洞见或灵机一动？我们不确定这里的洞见或灵机一动是指天才相对于普通人而言的能力还是某种超越人类的能力，是指超越经典物理抑或是超越任何物理理论可解释的现象。因此，仅仅这几条标准尚不足以作为能行或机械的精确定义。

20世纪30年代，哥德尔（Gödel，Kurt）、丘奇（Church，Alonzo）和图灵（Turing，Alan M.）分别以看似非常不同的方式给出了关于能行可计算函数的严格定义。它们分别是递归函数（recursive function）、λ-可计算函数（λcomputable function）和图灵机可计算函数（Turing computable function）。

λ-演算

λ-可计算基于丘奇发明的λ-演算（λ-calculus）。λ-演算由一组递归定义的λ-表达式（λ-expression）和若干归约规则组成。

定义　1.3（λ-表达式）　假设我们有可数无穷个变元。

（1）每个变元x是λ-表达式；

（2）如果x是变元，t是λ-表达式，那么λx.t是λ-表达式，我们称之为一个λ-抽象；

（3）如果t，s都是λ-表达式，那么ts是λ-表达式，我们称这是一个应用；

（4）除此以外没有别的λ-表达式。

直观上，λ-抽象是一种函数构造方式。例如，λx.x+1表示输入x输出x+1的函数，也即后继函数。而应用表示一个将一个变量输入一个函数得到的值。例如，（λx.x+1）x表示将x输入后继函数得到的值，也即x+1。对应用的直观的理解由接下来要定义的β-归约（β-reduction）来刻画。

类似谓词逻辑，λ-演算中也有变元的自由出现和约束出现的概念，可以被递归定义如下。

定义　1.4（自由变元（λ-演算））

（1）x中有且仅有自由变元x；

（2）λx.t中的自由变元是除x以外的t中的自由变元，此时我们称t中的x是在λx.t中约束出现的或λx.t中出现的x是一组约束变元；

（3）ts中的自由变元是t中或s中的自由变元。

直观上，x是自由变元即没有出现在某个λx的辖域中而被“约束”住。

我们称λ-表达式t与s是α-等价的或t是s的α-归约（α-reduction），当且仅当s是通过替换t的若干组约束变元得到的。这类似于谓词逻辑的约束变元替换定理（参见（郝兆宽、杨睿之、杨跃，2014，p.81））。

接下来，我们定义一个关于λ-表达式的正则代入算子。

定义　1.5（正则代入（λ-演算））　假设x，y是变元，t，s，r是λ-表达式。我们定义：

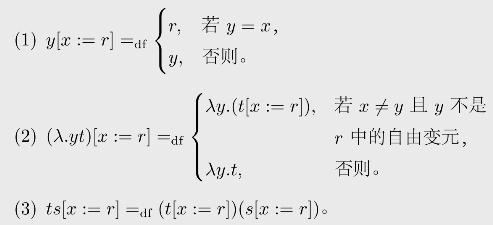
其中，唯一需要解释的是第二条子句。直观上，正则代入仅替换自由变元。如果x等于λy.t中的y的话，其中的x就是约束出现的，因而不作代入。另一方面，如果y是r中的自由变元，那么如果用r代x就会使得r中原本自由出现的y变得约束出现了，这会造成λ-表达式预期语义的意外变化。例如，假设x/=y，则λy.x表示一个常值为x的函数，如果y不在r中自由出现，那么λy.x[x：=r]=λy.r是一个常值为r的函数。但如果r=y并且我们允许它代替x，就会得到λy.y，变成一个等同函数了。

我们定义，S是T的β-归约当且仅当存在T的一个子表达式（λx.t）r，使得S是通过将T的某一处（λx.t）r替换为t[x：=r]得到的。直观上，t[x：=r]就是把函数λx.t应用到r所得到的“计算结果”。我们说两个λ-表达式t，s是β-等价的，当且仅当t=s或存在一个有穷序列〈s0，...，sn〉使得：s0=t，sn=s，且对任意0≤i＜n，要么si是si+1的β-归约，要么si+1是si的β-归约。

接下来，我们运用λ-表达式来表达一些算术对象。首先是自然数。

定义　1.6（丘奇数）

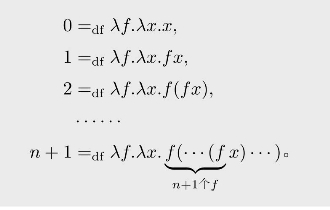
直观上可以这样理解：自然数被定义为一些关于函数的函数，0把所有函数映射为等同函数，n+1把函数f映射为对其自身做n次复合得到的函数。由此，我们可以定义后继函数为

succ=dfλn.λf.λx.f(nfx)，

定义加法函数为

add=dfλm.λn.λf.λx.mf(nfx)，

定义乘法函数为(www.daowen.com)

mult=dfλm.λn.λf.m(nf)。

定义　1.7（λ-可计算）　令F：N→N是自然数上的函数。我们说F是λ-可计算的，当且仅当存在一个λ-表达式f，使得对任意n，m∈N，有F（n）=m当且仅当fn与m β-等价。

更多关于λ-演算的内容可以参考（Alama，2016）和（Barendregt，2012）。

递归函数

递归函数　是通过递归定义的一类函数。其中，初始函数包括零函数

Z(x0,...,xn)=0、

后继函数

S(x)=x+1

以及投影函数

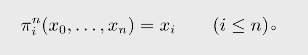
原始递归函数是由初始函数通过函数复合和原始递归生成的函数。而递归函数的构造还允许使用正则极小算子（regular μoperator）。更详细的介绍参见（郝兆宽、杨睿之、杨跃，2014，第七章）。

我们现在知道，这些刻画都是彼此等价的。这给了我们很强的经验证据，即这些定义的确正确刻画了能行或机械概念。这也就是人们所说的丘奇-图灵论题（Church–Turing thesis）。然而，在这些等价的定义中，图灵通过图灵机（Turing machine）所做的刻画被认为是最符合人们对能行或机械过程的直观的。哥德尔曾给予图灵的工作以高度评价，并常把图灵的刻画作为所有这些等价刻画的代表。根据王浩的报道（Wang，1996，7.3.1），哥德尔曾说：“我们之前就已经有了关于机械过程的精确概念，但直到了解了图灵的工作之后，我们才清晰地感知（perceive）到它。”

由于篇幅原因，这里仅简单介绍图灵机的定义、整篇文章的结构和论证思路，希望可以将（Turing，1937）作为一篇分析哲学的范文呈现给读者。

图灵机是一个严格的数学概念，一台图灵机由有穷字母表、有穷状态集、有穷指令集决定。直观上来说，图灵机运行在一条有无穷个方格向左右延伸的纸带上，有一个读写头可以在纸带上读写字母表中的字母，图灵机在每个时刻都处于状态集中的某个状态下。图灵机根据指令集、当前读到的字母和当前状态来决定下一步的操作，可以是让读写头向左或向右移动一格或在当前方格擦写一个字母，如图1.2所示。更详细的介绍可以参考（郝兆宽、杨睿之、杨跃，2014，p.132）。

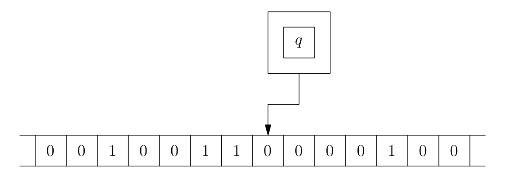
图1.2　图灵机

图灵论文的第一节直截了当地给出了计算机器（computing machine）的数学定义，也即我们现在所说的图灵机的定义。该节刻意回避了关于该定义是否符合某种直观的讨论：“直到第九节之前，我们不会真正地去为这里给出的定义辩护。”（Turing，1937，p.231）第二节进一步定义了什么样的计算机器是自动机器（automatic machine），以及什么是循环（circular）和非循环（circle-free）的机器。前者就是我们现在所说的确定性的图灵机（deterministic Turing machine），它在每一种情况下至多有一条合适的指令指导其下一步操作，因为如果有多条的话，就需要外界干涉来选择执行哪一条指令。循环的机器可以被大致类比于一个会陷入死循环或无进一步指令的计算机程序。一个可计算的数（computable number）就是由一个非循环的机器写下来的无穷01序列。^[18]

在第三节中，图灵给出了计算机器的一些例子。例如，能写出0 1 0 1 0 1...和0 0 1 0 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1...等01序列的非循环自动机器。第四节则是介绍了一些描述计算机器的缩写方式以方便写出更复杂的机器。这两节主要是通过直观的例子让读者熟悉前两节的定义，也为接下来的证明做准备。

第五节给出了对所有可计算01序列的一个枚举。实际上是给出了对图灵机的编码，并通过这些编码枚举所有图灵机机器运行结果，这使得第六、第七节关于通用图灵机的构造成为可能。第八节运用通用图灵机构造定义了不可计算的对角线函数。由此，如果假设丘奇-图灵论题成立的话，我们之前的问题得到了否定的答案，即存在不可计算的函数，甚至我们可以严格定义一个不可计算的函数。

第九节可能是全篇最精彩的部分。在本节中，图灵尝试为丘奇-图灵论题辩护。我们知道，这不可能是一个数学证明，因为无论是“能行的”还是“机械的”都是模糊不清的。这是关于某个严格的形式化定义是否正确地刻画了一个模糊的非形式概念的哲学论证。图灵在本节开篇就明确了这部分内容的定位。

【本文】到此为止尚未试图证明“可计算的”数囊括了所有会被自然地认为是可计算的数。对此，所有可以被给出的论证都注定是从根本上诉诸直观的，也因此是在数学上不令人满意的。（Turing，1937，p.249）

图灵区分了三种“从根本上诉诸直观的”论证：

（1）直接诉诸直观的论证；

（2）证明两种不同的定义等价；

（3）给出一大类“被自然地认为是可计算的数”，并证明它们是可计算的。

其中，后两条都是间接地诉诸直观的，即考虑人们对于那些直观的理解所形成的经验。第二条是对丘奇-图灵论题最常用的论证，即人们基于各自的直观给出了关于“能行”和“机械”的定义，通过经验归纳这些定义，发现它们互相等价，以此作为所有可能的定义全都刻画了同一个直观的经验证据。第三条是指收集大量人们通过各自直观认定为可计算的函数并证明它们是图灵可计算的，从而经验地使人相信图灵可计算概念确实囊括了所有可能“被自然地认为是可计算的”东西。这两种归纳都是仅涉及正面证据，可以加强我们对于丘奇-图灵论题的信心——正如每探测到一次引力波或其他时空扭曲事件符合爱因斯坦（Einstein，Albert）的预测就会增加我们关于该理论正确刻画了物理世界规律的信心一样。

图灵在第九节中给出的论证是直接诉诸我们对于“能行”或“机械”的直观的。其中涉及一个数学证明，证明了存在皮亚诺算术（Peano arithmetic）的一个有穷部分PA-使得：一个函数是图灵机可计算的，当且仅当能被PA-表示。^[19]这本身可以作为上面所说的第（2）种论证的论据，同时也可作为整个第九节直接诉诸直观的论证的一部分。接下来，笔者试着简单重现这部分论证。

图灵显然预设了第18页提到的关于能行或机械过程的标准（4），即能行过程必须是原则上人能完成的（能行可计算⇒原则上人能计算）。检验图灵机的定义容易接受凡是图灵机可计算的确实是一般认为的可计算的（图灵机可计算⇒能行可计算）。如果能论证所有原则上人能完成的计算过程也可以由图灵机完成（原则上人能计算⇒图灵机可计算），那么就可以得到“图灵机可计算⇔能行可计算”了。要论证“原则上人能计算⇒图灵机可计算”，理想的情况是“原则上人能计算”有一个严格的数学定义。然而，这样的定义是否合适仍然需要辩护。图灵在这里以一套精彩的分析终结了无穷倒退。

图灵从对一个理想的计算者（computer）^[20]的计算过程的分析出发，试图将她的“操作分解为基本的‘简单操作’以至于很难想象再怎么继续划分了”（Turing，1937，p.250）。

首先，一个计算者总是需要使用一些纸张来工作。其次，需要有一套符号（字母表）供计算者在纸张上记录。我们可以假设纸上画着方格，符号必须写在方格中，正如儿童的写字练习簿一样。由于我们可以证明使用方格二维展开的纸张（无论是一片有无穷个格子二维展开的纸，还是无穷张有穷格子的纸张的序列）与使用一维的纸带（即纸带被分为格子向左右无穷展开）工作没有本质的区别。^[21]不妨假设计算者总在一维纸带上工作，并且可以假设字母表总是有穷的。

图灵关于符号有穷的论证

有趣的是，图灵在（Turing，1937，p.249）脚注中关于“能被印刷出来的符号是有穷的”的论证并没有像当代物理主义者那样直接诉诸普朗克长度（Planck length）下测不准等物理结果，而是提供了一个有趣的数学证明。

图灵假设符号总是被印刷在一个1×1的方格上的，即所谓的符号都是[0，1]×[0，1]的一个子集。为了刻画符号之间的区别，图灵假设符号都是勒贝格可测（Lebesgue measurable）子集。即使如此，如果作为集合来考虑，也会有（这是一个非常大的无穷）个不同的符号。但有些符号之间恐怕很难区分。图灵将符号之间的距离定义为两个符号（集合）对称差^[22]的测度。例如，图1.3中的白色部分是符号“符”与“号”的对称差。由此，我们就得到了一个由所有符号组成的度量空间（metric space）。这是一个紧致的空间，因此不存在两两不交的无穷邻域集。

图1.3　符号间的距离

因此，如果我们考虑到识别问题，即把某个符号的某个邻域中的（如距离它小于10-1000的）所有符号识别为同一个符号，并且不允许混淆（即那些邻域两两不交）的话，那么无论识别精度多高，也只能分辨有穷个符号。换句话说就是：“如果我们允许无穷多个符号的话，那么符号之间的距离会任意小。”（Turing，1937，p.249）

如果字母表总是有穷的话，具体限制符号个数也变得不重要了。因为，“总是可以用符号序列来代替一个符号”。计算者在某一时刻会观察到一些纸带上的符号。然而，她在同一时刻至多观察到一定数量的符号。若如此，假设她每个时刻只能观察到一个符号也不会有本质的差别。

此外，计算者某一时刻的行为不仅仅取决于她所观察到的符号，还关系到她当下的心灵状态（state of mind）。图灵意识到这是一个复杂的对象，想要从生理学等角度来分析它还不太现实。这里，图灵天才地设想了心灵状态的一种外部对应，而不是像当代一些心灵哲学家、脑科学家一样妄图用扫描大脑活跃片区等方法来解释心灵。

计算者总是可以暂停她的工作然后继续这项工作。如果她暂停了她的工作，她必须留下一条指示笔记（note of instructions），以某个标准形式书写，说明这项工作如何继续下去。这条笔记就是“心灵状态”的对应。我们假设这个计算者工作得如此断断续续以至于她每次坐下只能工作至多一步。指示笔记必须让她可以进行一步并且写出下一条笔记。（Turing，1937，p.253）

基于类似符号有穷的理由，人的“心灵状态”或其对应的“指示笔记”也必须是有穷的。否则，“其中的某些会变得‘任意接近’以至于被混淆”（Turing，1937，p.250）。只是这里我们没法像字母表那样把心灵状态的个数限制为某个特定的自然数。

图灵宣称计算者的每一步操作“完全取决于”她的当时的心灵状态（或指示笔记）以及观察到的纸带上的符号。她能做的操作，当被拆分得尽量简单时，无非是：（a）改变纸带上的一个符号；（b）改变关注的方格。我们可以假设计算者在每一步观察的方格和可能改变其中符号的方格都只有一个，而进一步假设这两个方格是同一个也不会带来本质的不同。此外，有理由假设当我们将所关注的方格切换到另一个时，这两个方格的距离总是在某个特定范围之内，如不超过109格。而这与假设每次只能将注意力移至相邻方格上是没有本质区别的。此外，当执行这些操作时，计算者的心灵状态也可能会改变。因此，“最一般的简单操作总是以下两者之一”：

（A）改变（也可能不改变）当前关注的方格里的符号，同时改变（也可能不改变）心灵状态；

（B）改变关注的方格为左右某个方格，同时改变（也可能不改变）心灵状态。

因此，计算者进行计算某个时刻的系统状态（state of system）可以通过一个简单的表达式（符号序列）来描述，它包括纸带上的符号序列（有穷）、目前关注的方格在该序列上的位置以及当前的指示笔记。图灵又将这个表达式称作状态公式（state formula）。根据图灵的假设，某一步的状态公式必须完全取决于上一步的状态公式，并且这种对应关系（函数）能够在“函数演算”（functional calculus，不妨就理解为PA-）中表示出来。又根据PA-可表示与图灵机可计算的等价性，计算者的整个计算过程也就是图灵机可计算的了，从中不难提取出她的计算结果。因而，“原则上人能计算⇒图灵机可计算”。

严格来说，图灵的论证仍然有可商榷的地方。例如，假设能行可计算的必须是原则上人可计算的；假设计算者的操作总是完全取决于当前的心灵状态和观察到的符号；以及假设心灵状态总是有穷的。^[23]然而，图灵的整个分析过程（包括将能行或机械过程归约为一个理想的计算者的计算过程，以及对该计算过程的尽可能的拆解，对每个“不失一般性”的论证）既严谨又充满智慧，不失为分析哲学史上的典范之作。

以上，笔者介绍了从弗雷格到图灵等人的工作。这些工作大多被认为是现代逻辑学奠基性的成果，也大多在哲学界受到广泛重视，甚至被奉为经典。这些工作是数理逻辑与分析哲学共同之诞生的见证。不仅如此，它们或许是第一批见证了自笛卡尔（Descartes，René）、莱布尼茨乃至康德以来的梦想——让哲学成为一门可以进步的科学——是可实现的工作。