“真”从某种意义上说是一个终极哲学概念。因为，按照日常的理解，似乎所有的概念都可以被归约到“真”。即任给一个概念P、一个对象a，问a是否落在P之下，即问句子“a落在P之下”是否落在“真”之下。通过更细致的考察容易发现，日常的理解会产生一些问题。例如，我们取P为“真”概念本身，而a指称“a并非落在P之下”这句话，就会产生所谓的说谎者悖论。关于“真”概念的思考分化出诸多真理论，如真的对应理论（the correspondence theory of truth）、真的融贯论（the coherence theory of truth）、真的冗余论（the deflationary theory of truth）等。塔斯基（Tarski，Alfred）的真定义并不依附任何特定的真理论。相反，当代逻辑哲学关于真理论的任何讨论几乎都无法绕开塔斯基的形式定义。

塔斯基真定义最早正式发表于波兰语论文《演绎科学语言中的真概念》（Pojęcie prawdy w językach nauk dedukcyjnych，Tarski，1933）。^[12]塔斯基真定义主要的特点是采用了一种合成的（compositional）方式根据句子的结构来确定其真值，并且塔斯基试图在定义中避免涉及语义（semantic）概念而只采用语法（syntactic）概念，由此真可以作为其他语义概念的基础。

塔斯基真定义

塔斯基1933版的真定义只适用于“按科学方法构造的语言”，也即类似弗雷格概念文字的形式语言。并且，要求存在比该语言更高阶的元语言。对目标语言的真定义发生于元语言（metalanguage）中。塔斯基所描述的元语言至少包括目标语言所有语法部件的对应（翻译）、必要的集合论或类型论概念（以谈论目标语言的语法并使得我们现在所说的递归定义得以可能），以及一个用来表示真的一元谓词，如T。塔斯基所说的元语言其实是包含了形式语言、公理和推演规则的一个形式系统。

在进行真定义之前，塔斯基首先定义了一套记法来指称语言中的公式，同时揭示公式的结构。例如，用ιk，l表示由二元关系符号⊂，变元符号（即弗雷格的自变量）vk，vl相连组成的符号序列（塔斯基首先以一个谈论类的对象语言为例，其中非逻辑符号只有一个二元关系符号⊂）；用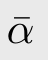表示¬连上公式α得到的符号序列；用α+β表示∨，α，β按顺序连接而成的符号序列；∩k α表示∀，vk，α连成的序列。我们现在一般分别用vk⊂vl，¬α，α∨β和∀vkα来指称这些公式，后文也将沿用这些现代表示方式。这些就是塔斯基所谓的结构描述名（structural descriptive name）。事实上，塔斯基通过这一系列定义试图强调的是，对象语言对象的结构描述可以在元语言中完成，包括定义什么是公式中的自由变元（free variable），以及把句子定义为不含自由变元的特殊公式。我们现在知道，集合论、类型论甚至算术语言就已经能够谈论这些语法概念了。

定义真必须通过一个二元的中间概念：满足。它是关于一个赋值（assignment）和一个公式的二元关系。其中赋值指的是对语言中的变元符号的解释，即把语言中的每个变元映射为一个个体对象。塔斯基首先定义，一个赋值v满足一个公式φ，当且仅当有下列情况之一发生：

（1）存在变元x，y使得φ=x⊂y，且π（⊂）v（x）v（y）；

（2）存在公式α使得φ=¬α，且v不满足α；

（3）存在公式α，β使得φ=α∨β，且v满足α或者v满足β；

（4）存在变元x和公式α使得φ=∀xα，并且对任意赋值w，如果w与v关于除x之外的变元的赋值一样，那么w就满足α。

按照塔斯基的想法，上面的定义发生在一个元语言中。显然，该元语言除了能给出句子的结构描述名之外，还必须能谈论（可能是无穷对象的）赋值函数。注意，π（⊂）是对象语言符号⊂在元语言中的翻译。π（）其实是元元语言（metametalanguage）的表达式，用来表示那个从对象语言到元语言的翻译。而所谓合成的定义，即该满足关系仅依赖于公式φ的最外层结构，以及v与φ上一层子公式的满足关系。

由满足关系就可以定义：一个句子σ是真的，当且仅当任意赋值v都满足σ。

从定义子句（4）不难看出使用“满足”这个中间概念是必要的。因为一个形如∀xα的句子是否为真，依赖于其子结构α的情况，而α可能并非句子，无法直接谈论真假。

塔斯基在之后又给出了论域限制版本的真定义，即将赋值限制为将变元映射到一类个体对象。这更接近于现代运用集合论语言表述的模型论中的真定义。因为，在类型论或二阶算术语言中，所谓个体（individual）有明确的所指，即一阶的对象或自然数，而集合论语言中没有这样一类特殊的对象。我们之后会看到，如果让对象语言变元的所指遍历元语言变元的所指，那就可能导致悖论。因此，有必要限制对象语言变元的赋值。

此外，当代模型论的真定义对非逻辑连接词（有固定的解释）非变元（由赋值解释）的符号，如上例的⊂，有更一般的处理。我们姑且称这些为参数符号。参数符号主要有关系符号、函数符号和常量符号（零元函数符号）。我们不再要求参数符号在元语言中有固定的对应。一个n元关系/函数符号可以被解释为个体域上任何一个n元关系/函数。如果以集合论语言为元语言，个体域和对参数符号的解释，例如上面的函数π，都是在元语言中表达的。它们合起来就被称为一个结构（structure）。满足关系就成了关于结构、赋值和公式的三元关系，而“真”就成了关于结构和句子的二元关系。如果一句句子在一个结构中真，我们就称该结构是该句子的模型。这种现代模型论的真定义直到（Tarski and Vaught，1957）才明确给出。

事实上，除了详尽地给出真的形式定义之外，塔斯基在长达159页（按波兰语原版）的论文中，投入了相当大的篇幅解释这种合成的定义方式何以必要，以及为什么真定义只能在特定的形式语言中被给予。

使用结构描述名（structural descriptive name）来指称句子，是塔斯基真定义的主要特点。为了论证使用结构描述名的必要性，塔斯基以日常语言中使用引号名（quotation-mark name）来指称句子作为候选方案，并说明这是不合适的。如果用引号名来指称句子的话，塔斯基首先给出了一个例子：

为了让（1.1）成为真定义的一个例式，真定义就应该形如(www.daowen.com)

或

但是，这里引号名“p”应该被看作是一个完整的专名，事实上在日常的理解中指称了一个字母。“我们没有正当理由可以替换作为引用名一部分的‘p’中的字母（正如我们不可以替换“true”一词中的字母“t”一样）”（Tarski，1933，p.160）。换句话说，“p”中并不含有变元p。因此，由（1.2）可以得到“‘p’是真的，当且仅当α”以及“‘p’是真的，当且仅当¬α”，因而是矛盾的。而（1.3）的一个推论是：“p”是唯一的真句子。这显然是荒谬的。而如果可以在元语言中运用结构描述名来指称对象语言的句子，这种名称本身就携带了所指句子的语法结构的信息，并且这些信息正好是判定其真假所需要的全部信息，我们就可以期待一个关于真的语法定义了。

为了论证无法对特定的语言（如日常语言）给出恰当的真定义，塔斯基给出了关于真定义的两条标准。

第一条标准是形式正确（formally correct），即真定义必须有如下形式：

其中，φ是元语言中的公式，不能含有T。由于元语言中只有T这一个指称语义概念的符号（除非对象语言中已经有指称语义概念的符号了），所以对真的定义应该是不涉及其他语义概念的。直观上，φ可以看作是以x为输入的运算，它先判断x是不是一句句子的结构描述名，再解码其包含的结构信息并由此判断是否为真。

真定义必须符合的另一条标准是实质恰当（materially adequate），也即塔斯基的T-约定：“一个形式正确的对T的定义是恰当的”，则所有形如

的命题（“把其中的x替换为对象语言任意一句句子的结构描述名，把p替换为该句子在元语言中的翻译”）都可以由该真定义和元语言的公理推出。

塔斯基认为如果一种语言足够强，以至于能谈论自己的语义，尤其是真概念的话，就会出现前文所说的说谎者悖论。因而，关于日常语言的真定义是不可能的。也因此，关于某个语言的真定义只能是在更强的元语言中发生的，即我们期望元语言能谈论对象语言的语义，而对象语言必须不能谈论自己的语义。

具体而言。假设对象语言就是元语言，并且我们可以找到该语言中的一句句子σ和它的结构描述名┍σ┑，使得σ↔¬φ（┍σ┑）。由（1.4），σ所指称的句子似乎就是在说“我不真”，即¬T（┍σ┑）↔σ。再由（1.5），T（┍σ┑）↔σ）是该定义与元语言中那些公理的推论。因此，关于该语言的任何同时满足真定义标准（1.4）和（1.5）的真定义与公理矛盾。

这里的关键是找到“我不真”这句话和它的结构描述名。这在日常语言中是平凡的，而在算术或更强的形式语言中的存在性则是由哥德尔不动点引理（Gödel’s fixed point lemma）给出的。

引理　1.1（哥德尔不动点引理）给定语言L。令Σ是语言L的一个理论（句子集），并且Σ足以证明关于形式系统语法的诸事实，那么对任何L公式ψ（x）（其中只有x是自由变元），都存在一个L句子σ和它的结构描述名┍σ┑，使得下述句子是Σ的推论：

对哥德尔不动点引理的类似运用可以得到塔斯基真不可定义定理（Tarski，1936）。

定理　1.2（塔斯基真不可定义定理）令L为一阶算术语言，N是对L的标准算术模型解释。T⊂N是所有N解释下为真的句子的哥德尔编码（Gödel number，一种结构描述名）组成的自然数集合，那么T是N中不可定义的。

如果说逻辑学的研究目标就是掌握关于真的规律，那么对“真”本身的研究无疑是逻辑学的核心。哥德尔完备性定理（Gödel’s completeness theorems）和塔斯基真不可定义定理（Tarski’s undefinability theorem）须在接受塔斯基真定义的前提下才有其通常被理解的意义。这种赋予技术成果以意义的工作无疑是哲学的，它甚至可以在一定程度上与那些技术性工作相互独立。本例中，该定义的正式发表甚至晚于哥德尔完备性定理。^[13]塔斯基本人对这个工作的哲学属性有明确的自觉：

……当前的工作在方法论上脱离了主流研究。它的中心问题——构造真句子的定义并为真理论奠定科学的基础——属于知识论，并且构成了这一哲学分支的主要问题。因此，我特别希望这个工作将会激起知识论学者的兴趣，并且他能够给予该工作的成果以批评性分析并判断这些成果在该领域后续研究中的价值。我希望他不会因为这里的概念分析装置和所使用的方法（有些地方确实很难，并且迄今未在他所工作的领域被使用过）而气馁。（Tarski，1933，p.267）

塔斯基这里所说的方法无非是指包括递归定义在内的形式化方法。以今天的标准来看，塔斯基真定义并不算很复杂的工作，事实上他的工作在哲学界也的确如其所愿地激励了一批学者。