刘易斯（Lewis，Clarence Irving）由于其在《符号逻辑综述》（A Survey of Symbolic Logic，Lewis，1918）中对“蕴涵”概念的处理被认为是现代哲学逻辑奠基人，从而被接受为早期分析哲学的代表人物。而事实上，刘易斯在书中为自己设定的任务也是有关数学基础的。刘易斯批评却无奈接受了他那个时代的“纯数学不再关心公设和定理的真，且定义总是随意的”。但他坚持，一个符号逻辑系统“只有当其中的‘蕴涵’的意义是‘恰当的’（proper）时，它才能作为有效推理的标准”。（Lewis，1918，p.324）因此，他的主要目的就是寻找“蕴涵”的“恰当的”含义。

罗素和怀特海（Whitehead，Alfred North）在《数学原理》（Principia Mathematica，Whitehead and Russell，1913）中是这样解释“蕴含”的：“p→q等价于¬（p∧¬q），它是真的当且仅当并非p真且q假。”我们知道，这种解释会导致“真命题被一切命题蕴涵”以及“假命题蕴涵一切命题”。刘易斯将蕴涵的这种解释称作实质蕴涵（material implication），并指出实质蕴涵“显然是关于命题真值之间的关系，而不是命题的内容或含义之间的关系”。（Lewis，1918，p.326）。与此相对，他提出了一种称作“严格蕴涵”（strict implication）的概念。

我们知道，“蕴涵”是一种基础逻辑概念，通过归约的方法来解释往往或进入循环或毫无用处。对这类基础逻辑概念的解释方式有两种，一种是提供语义模型，另一种就是公理化的方法。^[10]刘易斯主要采取了公理化的方法。他给出了一个严格蕴涵逻辑的公理系统，其中既有表示实质蕴涵的符号⊂，也有表示严格蕴涵的符号。接着，他证明了实质蕴涵的公理系统是它的一个子系统。而严格蕴涵逻辑去掉实质蕴涵符号的部分构成了另一个子系统——日常推理演算（the calculus of ordinary inference）。后者接近刘易斯心目中对“蕴涵”概念“恰当的”的解释。

刘易斯是这样为严格蕴涵概念辩护的。首先，他利用他对实质蕴涵和严格蕴涵概念的公理化得到有关概念的很多推论，再在一系列案例中检视这些推论是否能够反映案例中的蕴涵概念。例如，q⊂（p⊂q）是实质蕴涵逻辑系统的一个推论，但是我们不会仅仅因为“2+2=4”而认为“月亮是由绿色奶酪做成的”蕴涵“2+2=4”。对严格蕴涵的辩护中，比较棘手的问题是日常推理演算系统中与实质蕴涵系统中类似的定理：～p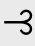（pq）和～-p（qp）。即“如果p是不可能的，那么p蕴涵任何命题q”以及“如果p是必然的，那么p被任何命题蕴涵”。为此，刘易斯必须论证，例如，“在‘蕴涵’的通常意义上，不可能的命题的确蕴涵任何东西”（Lewis，1918，p.336）。为此，他还是给出了几个自然语言中的具体例子说明关于严格蕴涵的这两个推论并没有什么不对。接着，他试图给出更一般的证据，以“p蕴涵非p”这个不可能的命题为例：(www.daowen.com)

【要证明】如果p蕴涵非p，那么p蕴涵任何命题q。我们已经证明了，如果q蕴含r，那么“q是真的且r是假的”蕴涵任何命题。因此，如果p蕴涵非p，“p是真的但非p是假的”，即“p是真的且p是真的”蕴涵任何命题q。但是p等价于“p是真的且p是真的”。因此，如果p蕴涵非p，p蕴涵任何命题q。（Lewis，1918，p.338）

刘易斯宣称他的证明“不依赖任何符号系统，只使用了日常逻辑中无可非议的原理”（Lewis，1918，p.336）。因此，这个看似自欺欺人的论证最终还是诉诸我们对逻辑概念的常识理解。

容易看出，刘易斯为严格蕴涵所做的辩护与弗雷格和罗素的工作有着类似的形式。《论指称》（Russell，1905）中处理的对象是指称短语，《算术基础》（Frege，1884）的问题是“数”这个概念，而《符号逻辑调查》的主题是“蕴涵”。它们都是语言的构件，并出现在一些哲学问题的陈述中，造成困扰。另一方面，它们解决问题的方式，也即所谓“语言分析”的结果都是给出一个更清晰明确的解释（或得到这种解释的一个能行方法）。例如，罗素给出了把含有指称短语的命题转化为不含这种短语的谓词公式的能行方法，弗雷格把“数”显定义为一种由概念组成的类，刘易斯则用一组公理来刻画“严格蕴涵”概念。所谓“语境原则”，不仅体现在最终给出的语义解释往往是语境敏感的^[11]，更多地是指他们的辩护策略。这类辩护实际上是一组思想实验，通过更换语境（变量）来检验各种备选的解释（理论假设），如果有且仅有一种解释能通过所有的检测，那么它自然是最似真的了。