由两个或多个大小不同的单位圆，小的在内，大的在外包含着相交于一点，有单螺旋式、双螺旋式、三螺旋式、以及多螺旋式等。

1.单螺旋式：两个大小不同的单位圆包含着相交于一点（见图1-8），三个大小不同并依次大小包含的单位圆，两两相交于不同的点（见图1-9）。

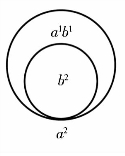
图1-8

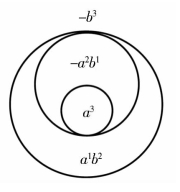
图1-9

图1-8 和图1-9 分属（a+b）类和（a-b）类，均还可以更多个大小不同的单位圆如此相交组合。

2.双螺旋式：双螺旋式组合体有双螺旋体、重复双螺旋体、再重复双螺旋体等。

（1）双螺旋体：两个相交于一点的同类单位圆被一个更大的同类单位圆包围，并分别与之相交于一点作整体极点的组合方式，如图1-10、图1-11所示的两类情况。

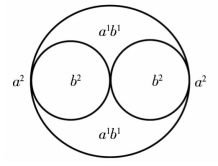
图1-10

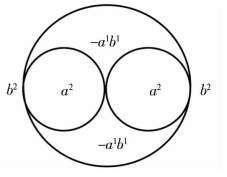
图1-11

图1-10 和图1-11 都有五个场区，图1-10 是（a+b）类，外阳内阴，有两个极点连接成的一个外场a2；图1-11 为（a-b）类，外阴内阳，有两个极点连接成的一个外场b2。

（2）重复双螺旋体：一个更大的单位圆，包含着两个相交于一点的同类双螺旋体（如图1-10 或图1-11），并分别与两个双螺旋体相交成不同极限点的组合方式，如（a+b）类图1-12所示。

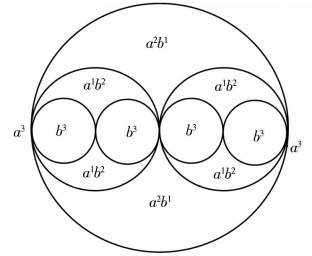
图1-12

（3）再重复双螺旋体：两个相交于一点的重复双螺旋体（见图1-12）被一个更大的圆包围，并分别相交于一点，成整体两极限点的组合，各场区强度相应提升，即再重复双螺旋体；再重复双螺旋体还可以相同方式重复组合成更多重双螺旋体。(www.daowen.com)

3.三螺旋式：与双螺旋式一样，但比双螺旋式多一个内小圆的牢固组合，有夸克式和中子式等。

（1）夸克式：三个相同并各自相交于一点的单位圆被一个更大的单位圆包围，又分别相交于不同点作极限点的组合，也有（a+b）类和（a-b）类，分别如图1-13 和图1-14所示。

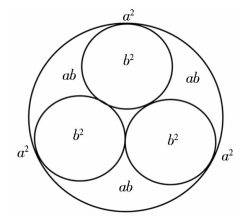
图1-13

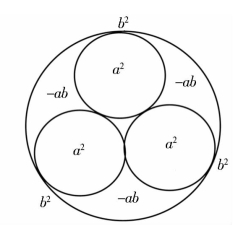
图1-14

图1-13 和图1-14 的构造相同，但字母排序及属性相反（省略了三圆间场区字母标注）。三螺旋式是最为致密和稳定的组合方式，把图1-13 称作正夸克，图1-14 称作夸克。

（2）中子式：就是把三个各自相交于一点的夸克或正夸克作为内小圆，以夸克形成的方式，被一个更大的单位圆包围，并各自相交于一点作极限点，各场区强度相应提升的相同方式重复组合，如图1-15所示。

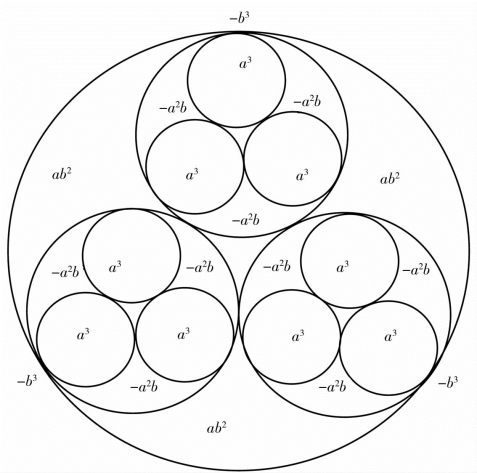
图1-15

图1-15 也是一个（a-b）类“三合一”组合体，外阴内阳（省略了三圆间场区字母标注），有三个极限点的外场-b3 表示整体中阴性强度最大的场，以及使整体转动的引力。

4.多螺旋式：一个二维平面只能容纳三个两两相交于一点的二维单位圆，如果是三维平面呢？就可以在二维平面中间上下垂直方向至少各加一个单位圆，使之成为立体球形——三维夸克。

球体单位圆形成：（a+b）（a-b）=a2-b2，是由两个属性相反且互为反物质的单位圆体相交合成，与（a-b）类属性一样，如图1-16所示。

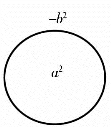
图1-16

有了球体单位圆才能有球体夸克，继而有三维中子、三维物体和三维世界。