1.完全平方和公式与完全平方差公式。

（1）完全平方和公式：（a+b）2=a2+2ab+b2，二元示图法认为：此等式左边为两个相交的（a+b）单位圆，右边三项式为两个圆相交后形成的三个层次的场区，如图1-4所示。

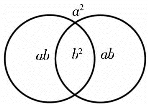
图1-4

（2）完全平方差公式：（a-b）2=a2-2ab+b2，与完全平方和公式不同的是，右边中间项为负值，如图1-5所示。

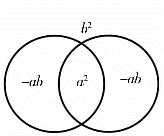
图1-5

以上两个公式的图示中，右边都是三个层次四个场区，其中的ab和-ab均各有两个场区，但两者属性相反，图1-4外阳内阴，从外向内阳性强度渐减而阴性强度渐增，中心场区为阴性b2；图1-5 外阴内阳，从外向内阴性强度渐减而阳性强度渐增，中心场区为阳性a2。

2.完全立方和公式与完全立方差公式。

（1）完全立方和公式：（a+b）3=a3+3a2b1+3a1b2+b3，表示为三个（a+b）单位圆相交，得四个层次八个场区的组合体，用二元示图法作图，如图1-6所示。(www.daowen.com)

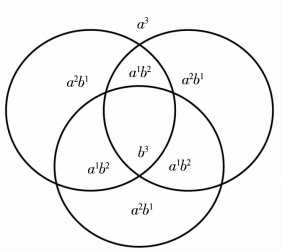
图1-6

（2）完全立方差公式：（a-b）3=a3-3a2b1+3a1b2-b3，表示为三个（a-b）单位圆相交，也是四个层次八个场区的组合体，运用二元示图法作图，如图1-7所示。

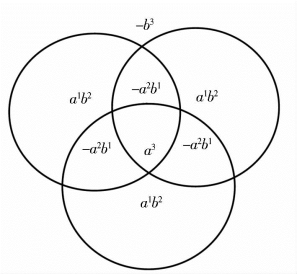
图1-7

从图中的字母和指数排列看，图1-6 和图1-7 的属性也是完全相反的，前者外阳内阴，后者则外阴内阳，且隔层为负值，中间层的负值场区为流体，最外层的负值场区为引力场。

3.二元示图法还可图示（a+b）与（a-b）的四次方、五次方，甚至更高次的方。参与相交的单位圆越多，其组合体场区也越多，场区数量等于公式右边各项系数之和。参与相交的单位圆与场区数量关系：x=2n（其中x为场区数量，n 是参与相交的单位圆数量）；从小到大，各次方公式的场区系数整体构成了“杨辉三角”。

以上图1-4 至图1-7 的每个图组中，参与相交的单位圆大小相等，把这种相交方式称作收发式；把若干大小不同的单位圆，且大圆包围小圆，两圆间相交于一点的组合方式，称为螺旋式；把若干大小不同的单位圆，且大圆包围小圆，两圆间没有相交点的组合方式，称为同心式。