前面讨论了线性回归问题，对线性情形我们有了一整套的理论与方法.在实际中常会遇见更为复杂的非线性回归问题，此时一般是采用变量代换法将非线性模型线性化，再按照线性回归方法进行处理.例如：

模型

其中a，b，σ2 为与t 无关的未知参数，只要令x=sin t，即可将上式化为一元线性回归方程式.

模型

其中a，b，c，σ2 为与t 无关的未知参数.令x1=t，x2=t2 得

它为多元线性回归的情形.

模型

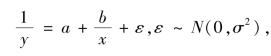
令y′=，则有y=a+bx′+ε，ε~N（0，σ2），即化为一元线性回归方程式.

模型

令x′=ln x，则有y′=a+bx′+ε，ε~N（0，σ2），又可化为一元线性回归方程式.

另外，还有下述模型

其中Q 为已知函数，且设Q（y）存在单值的反函数，a，b，σ2 为与x 无关的未知参数.这时，令z=Q（y），得

在求得z 的回归方程和预测区间后，再按z=Q（y）的逆变换，变回原变量y.我们就分别称它们为关于y 的回归方程和预测区间.此时y 的回归方程的图形是曲线，故又称为曲线回归方程.

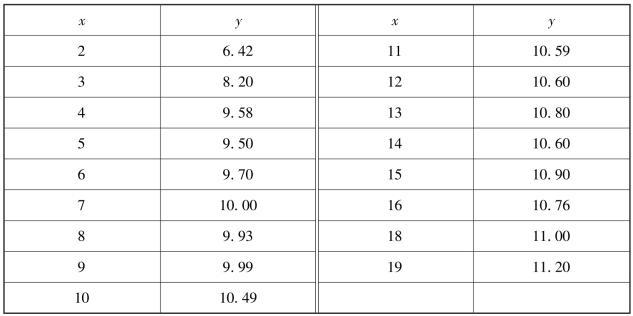
例10.5　某钢厂出钢时所用的盛钢水的钢包，由于钢水对耐火材料的侵蚀，容积不断扩大.通过试验，得到了使用次数x 和钢包增大的容积y 之间的17 组数据，见表10.5，求使用次数x 与增大容积y 的回归方程.

表10.5(www.daowen.com)

解　散点图如图10.5 所示.从图中可以看出y 与x 呈倒指数关系，ln y=a+b+ε，记y′=ln y，x′=，求出x′，y′的值（表10.6）.

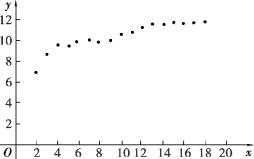
图10.5

表10.6

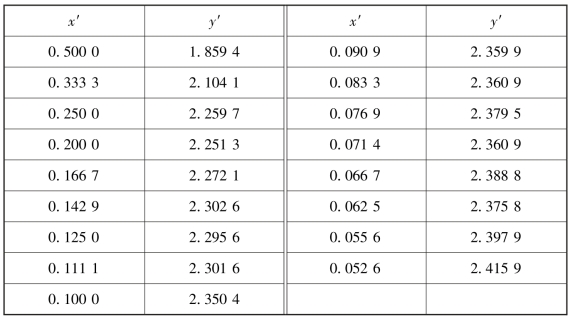
作（x′，y′）的散点图，如图10.6 所示.

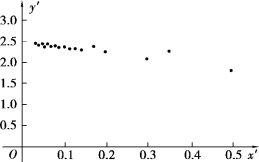
图10.6

可见各点基本上在一直线上，故可设

经计算，得

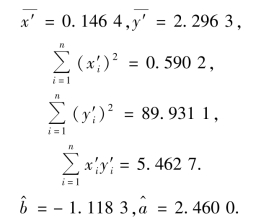
于是y′关于x′的线性回归方程为

换回原变量得

现对x′与y′的线性相关关系的显著性用F 检验法进行检验，得

检验结论表明，此线性回归方程的效果是显著的.