由于x 与y 并非确定性关系，因此对于任意给定的x=x0，无法精确知道相应的y0 值，但可由回归方程计算出一个回归值，可以以一定的置信度预测对应的y 的观察值的取值范围，也即对y0 作区间估计，即对于给定的置信度1-α，求出y0 的置信区间[称为预测区间（prediction interval）]，这就是所谓的预测问题.

对于给定的置信度1-α，可证明y0 的1-α 预测区间为

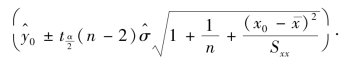
给定样本观察值，作出曲线

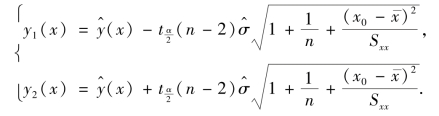
这两条曲线形成包含回归直线的带形域，如图10.2 所示，这一带形域在x=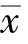处最窄，说明越靠近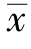，预测就越精确.而当x0 远离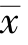时，置信区域逐渐加宽，此时精度逐渐下降.

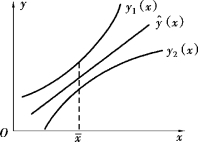
图10.2

在实际的回归问题中，若样本容量n 很大，在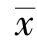附近的x 可得到较短的预测区间，又可简化计算

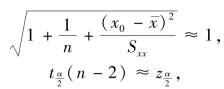
故y0 的置信度为1-α 的预测区间近似等于

特别地，取1-α=0.95，y0 的置信度为0.95 的预测区间为

取1-α=0.997，y0 的置信度为0.997 的预测区间为(www.daowen.com)

可以预料，在全部可能出现的y 值中，大约有99.7%的观测点落在直线与直线L1：y=所夹的带形区域内，如图10.3 所示.

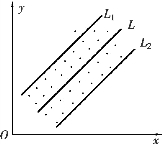
图10.3

可见，预测区间意义与置信区间的意义相似，只是后者对未知参数而言，前者是对随机变量而言.

例10.4　给定α=0.05，x0=13.5，问例10.1 中生产费用将会在什么范围.

解　当x0=13.5，y0 的预测值为

给定α=0.05，t0.025=2.306，

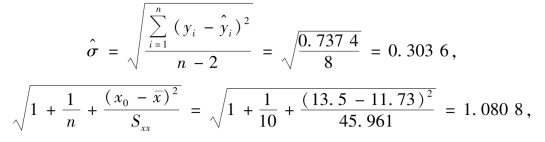
故

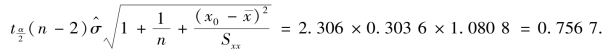
即y0 将有95%的概率落在12.467 4 ±0.756 7 区间，即预报生产费用在11.710 7 ~13.224 1万元之间.